35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
思考
二分模板题
class Solution:def searchInsert(self, nums: List[int], target: int) -> int:left = 0 right = len(nums)#[left,right)while left<right:mid = int((left+right)/2)if nums[mid] > target:right = midelif nums[mid] < target:left = mid + 1else:return midreturn left
BM21 旋转数组的最小数字(有重复数字)
思考
剑指offer上原题。数组划分为2个区间,二分搜索逐渐逼近最小值。遇到无法判断区间时,需要顺序逐个查找。
class Solution:def minNumberInRotateArray(self , nums: List[int]) -> int:# write code hereleft = 0right = len(nums)-1mid = 0while nums[left]>=nums[right]:if right-left == 1:return nums[right]mid = int((left+right)/2)if nums[left] == nums[right] and nums[left] == nums[mid]:res = nums[left]for i in range(left+1,right+1):if nums[i] < res:res = nums[i]return resif nums[mid] >= nums[left]:left = midelif nums[mid] <= nums[right]:right = midreturn nums[left]
- 搜索旋转排序数组 (无重复数字搜索指定target)
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
思考
根据mid值判断是左有序 还是 右有序。在有序的区间内进行二分查找。
class Solution:def search(self, nums: List[int], target: int) -> int:left = 0right = len(nums)-1#[left,right]mid = -1while left<=right:mid = int((left+right)/2)if nums[mid] == target:return midif nums[mid] >= nums[left]:#左有序if target >= nums[left] and target < nums[mid]:# 二分right = mid - 1else:left = mid + 1else:#右有序if target > nums[mid] and t arget <= nums[right]:left = mid + 1else:right = mid -1return -1
153.寻找旋转排序数组中的最小值(无重复)
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
思考
比有重复的要简单一点。两种方法。
方法1:剑指offer版本,比较容易理解:划分为2个区间,逐渐逼近结果。
class Solution:def findMin(self, nums: List[int]) -> int:left = 0right = len(nums)-1mid = 0while nums[left] > nums[right]:if right - left == 1:return nums[right]mid = (left+right)//2if nums[mid] >= nums[left]:left = midelif nums[mid] <=nums[right]:right = midreturn nums[0]
方法2:leetcode官方题解。
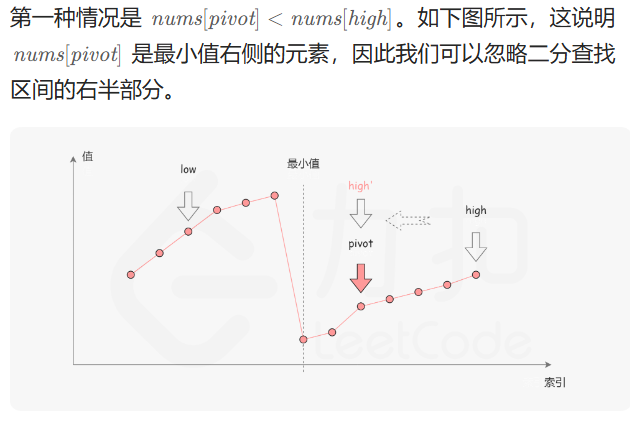
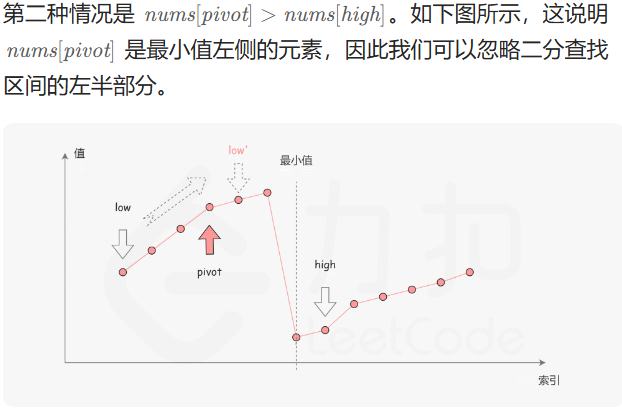
在二分查找的每一步中,左边界为 low,右边界为 high,区间的中点为 pivot,最小值就在该区间内。我们将中轴元素 nums[pivot] 与右边界元素 nums[high] 进行比较,可能会有以下的三种情况:

class Solution:def findMin(self, nums: List[int]) -> int:left = 0right = len(nums)-1mid = 0while left < right:mid = (left+right)//2if nums[mid] < nums[-1]:right = midelse:left = mid + 1return nums[left]
34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
思考
划分为2个区间 <target 和 >=target 来寻找左边界。
右边界通过寻找targe+1的左边界-1来代替。优雅
class Solution:def searchRange(self, nums: List[int], target: int) -> List[int]:def getRightBorder(nums, target):left = 0 right = len(nums)-1#right_border = -2while left<=right:mid = int((left+right)/2)if nums[mid] > target:right = mid - 1else:left = mid + 1return rightdef getLeftBorder(nums, target):left = 0 right = len(nums)-1#left_border = -2while left<=right:mid = int((left+right)/2)if nums[mid] < target:left = mid + 1else:right = mid - 1#left_border = rightreturn leftleft_border = getLeftBorder(nums, target)#right_border = getRightBorder(nums,target)right_border = getLeftBorder(nums, target+1) - 1if left_border == len(nums) or nums[left_border] != target:return [-1,-1]else:return [left_border,right_border]