本文记述了堆排序的基本思想和一份参考实现代码,并在说明了算法的性能后用随机数据进行了验证。
◆ 思想
J.W.J Williams 提出了堆排序的算法,该算法利用了二叉堆有序的性质,将排序的过程分为先构建堆再排序的两个阶段。
先构建堆。从当前待排序范围一半的位置开始向第一个位置扫描,用下沉操作处理每个位置的元素。每操作一个位置后,以该位置为根节点的子堆就是堆有序的。当扫描完范围的第一个位置后,整个待排序范围就达到了堆有序的状态,即完成了堆的构建。
再排序。将当前堆中的最大元素放到堆底的最后位置,即交换待排序范围的第一个位置的元素和最后一个位置的元素。然后将待排序范围的第一个位置至倒数第二个位置视为新的堆,对新的堆顶元素做下沉操作后,新堆也恢复到堆有序状态。重复以上操作,直到待排序范围只有一个元素为止,排序结束。
◆ 实现
排序代码采用《算法(第4版)》的“排序算法类模板”实现。(代码中涉及的基础类,如 Array,请参考算法文章中涉及的若干基础类的主要API)
// heap.hxx...class Heap
{...template<class _T,class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type>staticvoidsort(Array<_T> & a){int N = a.size();for (int k = N/2; k >= 1; --k) // #1__sink__(a, k, N);while (N > 1) {__exch__(a, 1, N); // #2--N;__sink__(a, 1, N); // #3}}...template<class _T,class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type>staticvoid__sink__(Array<_T> & a, int k, int n){while (2*k <= n) { // #4int j = 2*k;if (j < n && __less__(a, j, j+1)) ++j; // #5if (!__less__(a, k, j)) break;__exch__(a, k, j);k = j;}}...template<class _T,class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type>staticbool__less__(Array<_T> const& a, int i, int j){return a[i-1].compare_to(a[j-1]) < 0; // #6}template<class _T,class = typename std::enable_if<std::is_base_of<Comparable<_T>, _T>::value>::type>staticvoid__exch__(Array<_T> & a, int i, int j){_T t = a[i-1];a[i-1] = a[j-1];a[j-1] = t;}...
从当前待排序范围一半的位置开始向第一个位置扫描,用下沉操作达到堆有序的状态(#1)。将当前堆中的最大元素放到堆底的最后位置(#2)。然后对新的堆顶元素做下沉操作后,使新堆也恢复到堆有序状态(#3)。该算法用的是二叉堆(#4),所以某个节点与其两个子节点相比较后,决定是否继续下沉(#5)。将 '<' 改为 '>',即得到逆序的结果(#6)。
◆ 性能
| 时间复杂度 | 空间复杂度 | 是否稳定 |
|---|---|---|
| N*log(N) | 1 | 否 |
◆ 验证
测试代码采用《算法(第4版)》的倍率实验方案,用随机数据验证其正确性并获取时间复杂度数据。
// test.cpp...time_trial(int N)
{Array<Double> a(N);for (int i = 0; i < N; ++i) a[i] = Std_Random::random(); // #1Stopwatch timer;Heap::sort(a); // #2double time = timer.elapsed_time();assert(Heap::is_sorted(a)); // #3return time;
}...test(char * argv[])
{int T = std::stoi(argv[1]); // #4double prev = time_trial(512);Std_Out::printf("%10s%10s%7s\n", "N", "Time", "Ratio");for (int i = 0, N = 1024; i < T; ++i, N += N) { // #5double time = time_trial(N);Std_Out::printf("%10d%10.3f%7.2f\n", N, time, time/prev); // #6prev = time;}
}...
用 [0,1) 之间的实数初始化待排序数组(#1),打开计时器后执行排序(#2),确保得到正确的排序结果(#3)。整个测试过程要执行 T 次排序(#4)。每次执行排序的数据规模都会翻倍(#5),并以上一次排序的时间为基础计算倍率(#6),
此测试在实验环境一中完成,
$ g++ -std=c++11 test.cpp std_out.cpp std_random.cpp stopwatch.cpp type_wrappers.cpp$ ./a.out 15N Time Ratio1024 0.009 2.252048 0.022 2.444096 0.048 2.188192 0.106 2.2116384 0.230 2.1732768 0.500 2.1765536 1.086 2.17131072 2.349 2.16262144 5.064 2.16524288 10.883 2.151048576 23.276 2.142097152 49.570 2.134194304 105.310 2.128388608 223.426 2.1216777216 474.822 2.13
可以看出,随着数据规模的成倍增长,排序所花费的时间将是上一次规模的 2.1? 倍,且在不断地变小。将数据反映到以 2 为底数的对数坐标系中,可以得到如下图像,
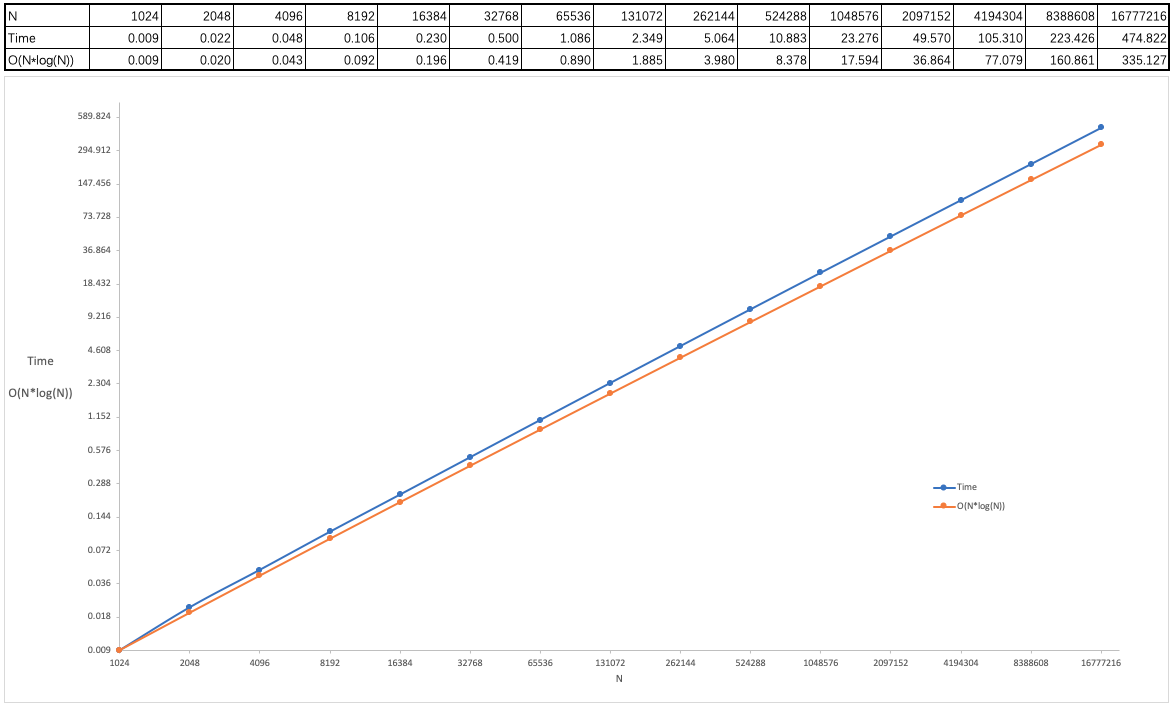
O(N*log(N)) 代表了线性对数级别复杂度下的理论排序时间,该行中的数据是以 Time 行的第一个数据为基数逐一乘 2 + 2/log(N) 后得到的结果(因为做的是倍率实验,所以乘 (2*N*log(2*N)) / (N*log(N)),化简得到 2 + 2/log(N),即乘 2+2/log(1024),2+2/log(2048),2+2/log(4096),... 2+2/log(16777216);因为是二叉堆,所以 log 的底数为 2)。
◆ 最后
完整的代码请参考 [gitee] cnblogs/18289928 。
写作过程中,笔者参考了《算法(第4版)》的堆排序、“排序算法类模板”和倍率实验。致作者 Sedgwick,Wayne 及译者谢路云。