👉🏻Stack Constructor

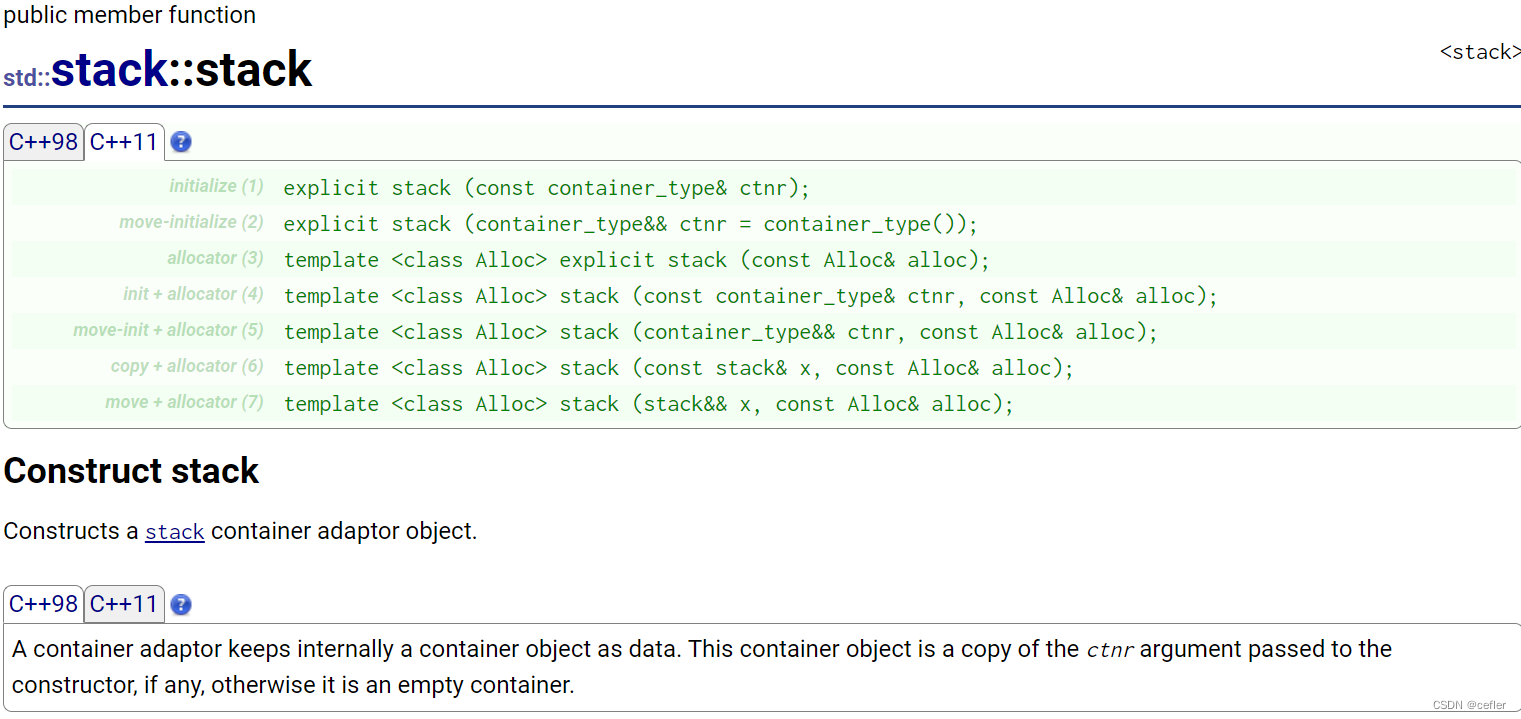
在这里插入图片描述
Stack官方文档

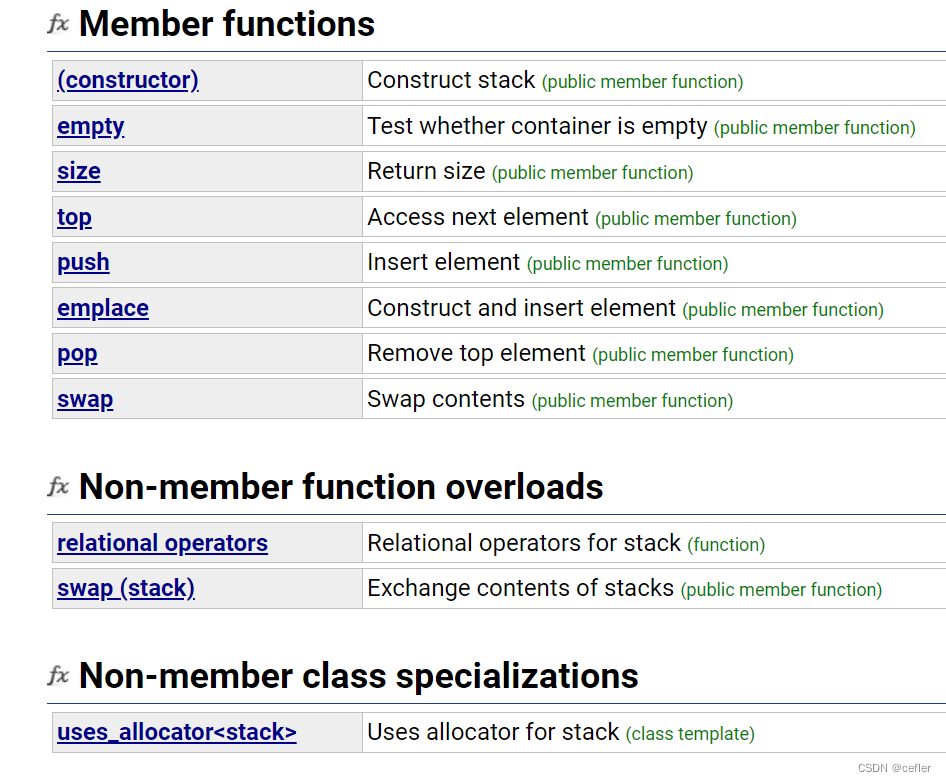
👉🏻Stack Member functions

在这里插入图片描述

👉🏻Queue constructor

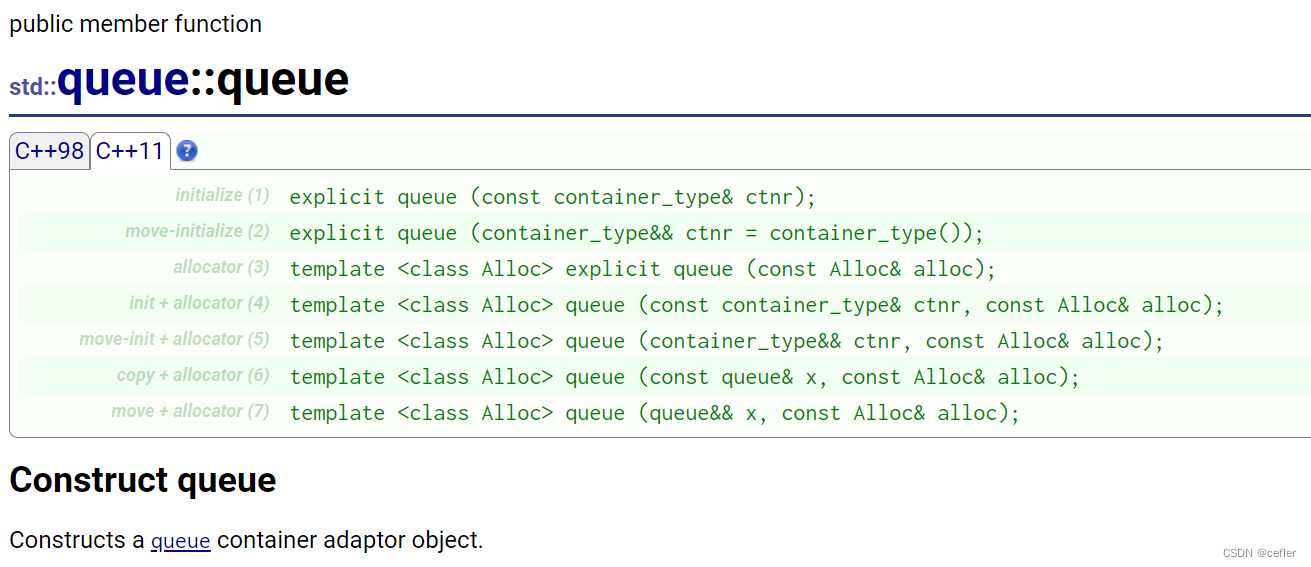
在这里插入图片描述
Queue官方文档

👉🏻Queue Member functions

在这里插入图片描述

👉🏻LeetCode题

最小栈

class MinStack {
public:MinStack() {//不需要写构造函数//自定义类型会去调用它自己的默认构造函数}void push(int val) {_st.push(val);if(_minst.empty()||val<=_minst.top()){_minst.push(val);}}void pop() {//如果_st的栈顶等于_minst的栈顶，_minst也要出栈if(_st.top()==_minst.top()){_minst.pop();}_st.pop();}int top() {return _st.top();}int getMin() {return _minst.top();}stack<int> _st;stack<int> _minst;
};

那么如果在st中插入很多重复的数据，我们还要再向_minst中插入吗？
其实我们这里可以构建一个结构体

struct CountVal{int _val;int count = 0;};

我们插入一个结构体，遇到相同的++count 即可

栈的压入、弹出序列

原题链接：栈的压入、弹出序列
MyCode:

class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param pushV int整型vector * @param popV int整型vector * @return bool布尔型*/bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {stack<int>  st;size_t popV_sz = popV.size();size_t pushV_sz = pushV.size();int i = 0, j = 0;int flag = 0;for(i=0,j =0;j<pushV_sz;j++){//先从栈里面先找while(!st.empty()){if(st.top()==popV[i]){i++;flag = 1;//找到了//找到后记得pop掉st.pop();}else {break;}}if(popV[i] == pushV[j]){i++;flag = 1;//找到了}else{st.push(pushV[j]);}}if(!flag)return false;//如果结束都找不到//接下来进入出栈匹配环节while(!st.empty()){if(popV[i++]!=st.top())return false;st.pop();}return true;}
};

思路思想：
在这里插入图片描述

其实后续发现无需flag,只要最后出栈环节匹配不上也不对。
所以优化掉flag后

class Solution {
public:bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {stack<int>  st;size_t popV_sz = popV.size();size_t pushV_sz = pushV.size();int i = 0, j = 0;for(i=0,j =0;j<pushV_sz;j++){//先从栈里面先找while(!st.empty()){if(st.top()==popV[i]){i++;//找到后记得pop掉st.pop();}else {break;}}if(popV[i] == pushV[j]){i++;}else{st.push(pushV[j]);}}//接下来进入出栈匹配环节while(!st.empty()){if(popV[i++]!=st.top())return false;st.pop();}return true;}
};

other version:
在这里插入图片描述

bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {stack<int> st;int pushi = 0, popi = 0;while (pushi < pushV.size()){//先入栈st.push(pushV[pushi++]);while (!st.empty() && st.top() == popV[popi]){popi++;st.pop();}}return st.empty();}
};