题目大意
\(n\) 个工厂,每个工厂有 \(p_i\) 的货物,货物运输一个单位距离的费用是 \(1\),工厂可以建造仓库,费用为 \(c_i\)。工厂与工厂 \(1\) 的距离为 \(x_i\)。要求将货物运送到下一个最近的仓库,求最小费用。
\(1\leq n\leq 10^6\)
思路
先考虑最基本的动规:
设 \(f_i\) 表示在这里建仓库时 \([1,i]\) 的转移与建造的最小费用。则有方程:
化简:
设 \(s_x=\sum_{i=1}^x p_i\),\(v_x=\sum_{i=1}^x x_ip_i\),则原式化为:
整理一下就是设函数 \(F_k(x)=-s_kx+f_k+v_k\),\(C_k=s_kx_k-v_k+c_k\) 则原式就转化成了斜率优化可以做的样子:
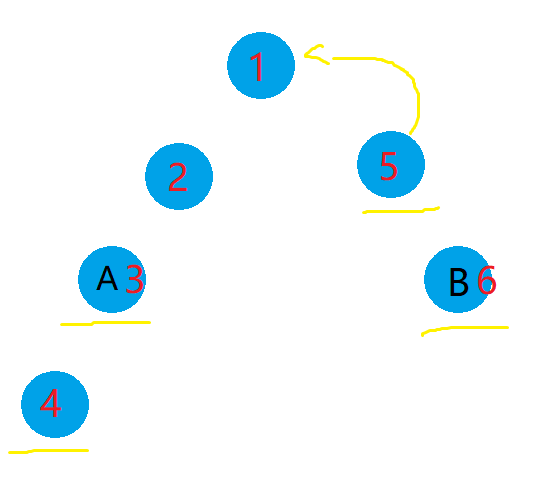
对于要求的 \(f_i\),维护 \(F_k\) 其中 \(k\in[0,i)\)。之后找到一个最优的 \(F_k\) 使得 \(F_k(x_i)\) 能取到最低点。换句话说我们维护的是一个凸包。像:

这里的紫色部分显然就是答案。之后考虑维护。
观察到 \(s\) 严格单调递增,即 \(F_k\) 的斜率 \(-s_k\) 严格单调下降,换句话说只要当前的这个函数不够优秀那我们以后都不再会选择了。可以考虑将函数维护成单调队列。发现凸包会被交点分成一段一段,则我们只要删除的时候发现交点大于 \(x_i\) 就可以舍去。则之后的 \(f_i\) 可以设成 \(f_i=F_{\text{front}}(x_i)+C_i\),其中 \(\text{front}\) 指单调队列队首。然后考虑插入 \(F_i\)。可以直接用当前的最后一个交点与次大函数与 \(F_i\) 的交点进行比较,如果小的话就可以继续出队列,直到更新不好为止,之后插入 \(F_i\)。
求函数交点很好求。对于 \(y_0=kx+b\) 与 \(y_1=px+q\) 来说它们的交点就是
特别的,在插入函数时如果它们的斜率一样就可以直接取截距小的那个,因为它们平行(或重合),当然取截距小的。
代码
#include<bits/stdc++.h>
#define v(u,x) (u.a*1.0*x+u.b)
using namespace std;
typedef long long ll;
typedef long double ld;
const ll MAXN=1e6+5;
struct Func{ld a,b;Func(ld _a,ld _b){a=_a;b=_b;}
};
ld jd(Func p,Func q){if(p.a==q.a){if(p.b>=q.b){return 1e18;} return -1e18;}return (q.b-p.b)*1.0/(p.a-q.a);
}
ll sxp[MAXN],sp[MAXN];
ll n;
ll x[MAXN],p[MAXN],c[MAXN];
ll f[MAXN];
deque<Func>dq;
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n;for(int i=1;i<=n;++i){cin>>x[i]>>p[i]>>c[i];sp[i]=sp[i-1]+p[i];sxp[i]=sxp[i-1]+x[i]*p[i];}dq.push_back(Func(0,0));for(int i=1;i<=n;++i){while(dq.size()>1){Func F=dq.front();dq.pop_front();if(jd(dq.front(),F)>x[i]){dq.push_front(F);break;}}f[i]=v(dq.front(),x[i])+sp[i]*x[i]-sxp[i]+c[i];Func nw=Func(-sp[i],f[i]+sxp[i]);while(dq.size()>1){Func F=dq.back();dq.pop_back();if(jd(dq.back(),F)<jd(dq.back(),nw)){dq.push_back(F);break;}}dq.push_back(nw);}ll ans=1e18;for(int i=n;i>=1;--i){ans=min(ans,f[i]);if(p[i]){cout<<ans<<endl;return 0;}}return 0;
}