『比赛记录』【LGR-193】洛谷 7 月月赛 IABC 362

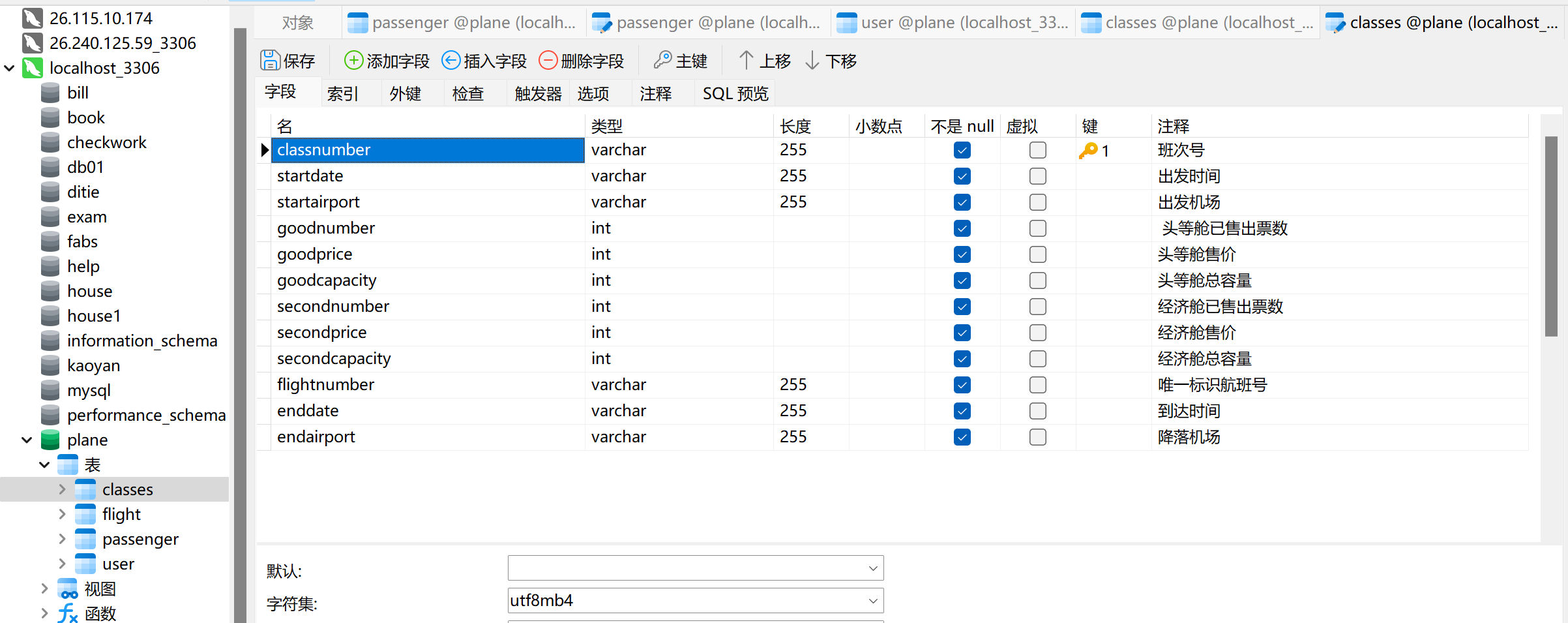
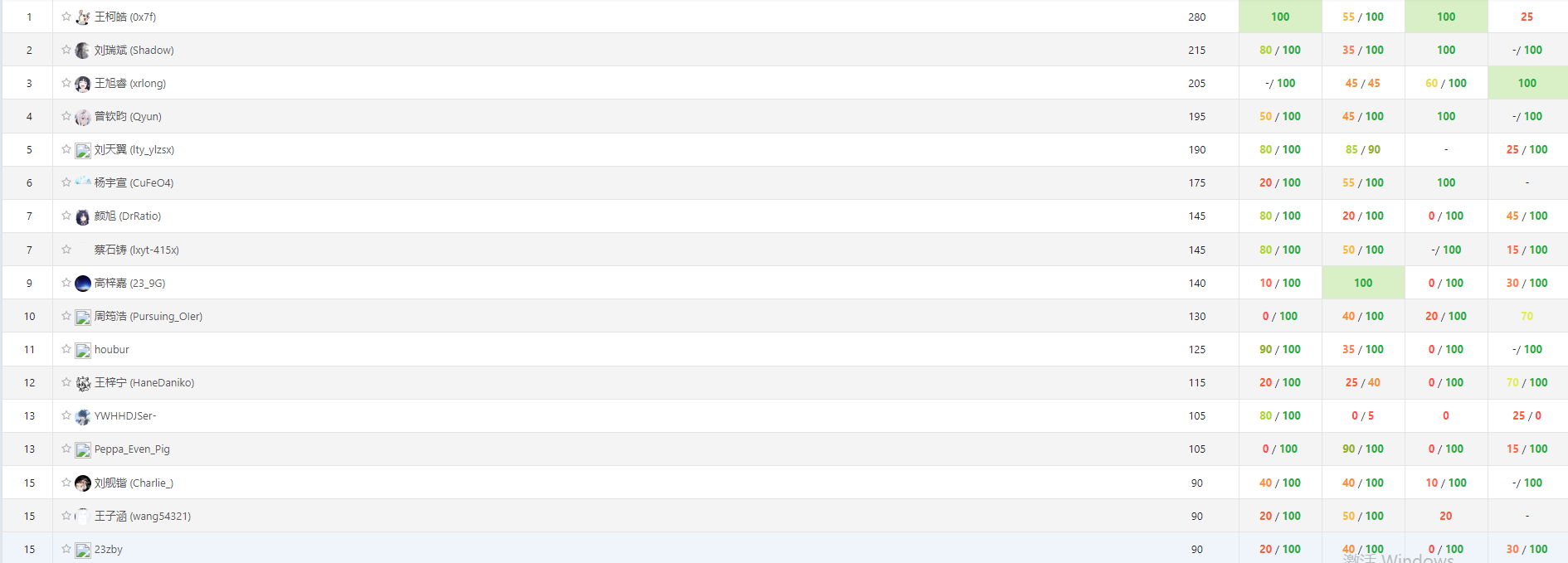
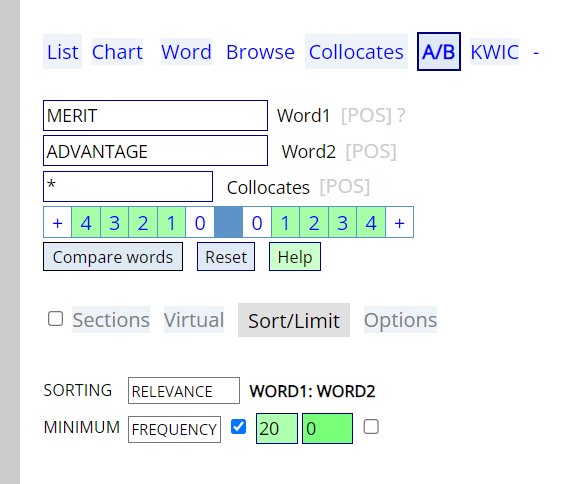
最舒服的一集

---

「CROI · R2」在相思树下 I

想了好久还是决定把这道题也写一下，毕竟赛事花了 \(40min\) 才解决。

思路

开比赛，看题面，很快啊，打了一个双端队列的做法，结果 MLE，然后人傻了二十分钟。

之后缓过神来开始推式子。我们把答案先看做操作后的第一个数，提供一个样例：

\[2\,\,2\,\,2\,\,1\,\,2 \]

结果为：

\[1\,\,1\,\,1\,\,9\,\,9 \]

这么看是不是看不出来什么，我们换个写法：

\[2-1\,\,4-3\,\,8-7\,\,16-7\,\,32-23 \]

再加上一个初始答案 \(1-0\)，是不是看出什么了？

我们设减法式子为 \(a-b\)，通过观察模拟发现一下结论：

当 \(op=1\) 时，\(a=2a\)；

当 \(op=2\) 时，\(b+=a\)，\(a=2a\)。

初始值 \(a=1\)，\(b=0\)。

于是我们就快乐地找到正解了。

Code：

#include<bits/stdc++.h>typedef long long ll;const int Ratio=0;
ll n,k;namespace Wisadel
{short main(){int T,op;scanf("%d",&T);while(T--){scanf("%lld%lld",&n,&k);ll a=1,b=0;for(int i=1;i<=k;i++){scanf("%d",&op);if(op==1) a*=2;else b+=a,a*=2;}printf("%lld\n",a-b);}return Ratio;}
}
int main(){return Wisadel::main();}

看来这种有简单方法但结论复杂的题确实不适合放在 T1，尤其是对我。

---

「CROI · R2」在相思树下 II

一道比 T2 简单的 T3。

思路

我们发现比赛流程图的形状是一棵完全二叉树，而题目所求的出每一轮次的进入范围限制也是从它的子比赛更新而来的，因此可以按类似线段树建图的方法直接处理出每一轮次的范围，最后 \(O(1)\) 查询即可。

我们先设 \(l_i\)，\(r_i\) 分别为第 \(i\) 个节点中至少有 \(l_i\) 个数比符合条件的值 \(x\) 小，至少有 \(r_i\) 个数比 \(x\) 大。

放一张图形式化一下：

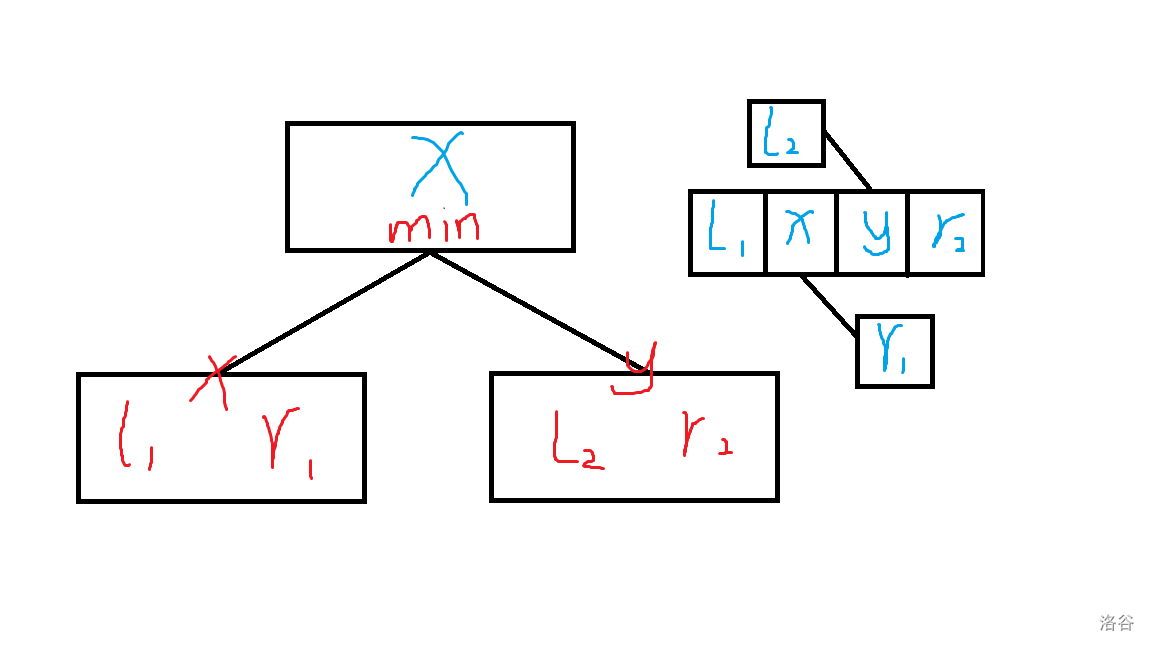
（图丑，轻喷）

我们以一个按照规则二比赛的节点举例：
假设胜者为 \(x\)，那么比赛后即拼凑后的范围块长右图那样。

更新时，首先已知有 \(r_1\) 个数需要比 \(x\) 大，有 \(r_2\) 个数需要比 \(y\) 大，同时要满足 \(x<y\)，所以最终这一节点的 \(r_i\) 值应为 \(r_1+r_2+1\)；

同时需要至少有 \(l_1\) 个数比 \(x\) 小，\(l_2\) 个数比 \(y\) 小，由获胜者为 \(x\) 我们可以推出 \(l_1<l_2\)，即 \(x\) 能取到更小的值，所以在这个节点中的左边界就是 \(x\) 子节点的左边界，但这是在假设 \(x\) 获胜的情况，所以真正更新时的 \(l_i\) 应等于 \(\min(l_1,l_2)\)。

按规则一比赛的节点同理，大家可以自己手动模拟下，最终转移式为：

\[l_i=l_{lson}+l_{rson}+1 \]

\[r_i=\min(r_{lson}+r_{rson}) \]

实现方面，由于二叉树的性质，我们根据节点长度 \(len\) 可知该节点所在的层数为 \(log_2 \,len\)。题目中只需要进入某一层即可，所以整层的范围就是该层所有块的左右边界值分别的最小值。

细节处理

每节点左右边界初始为 \(0\) 即无限制，每层左右边界初始为 \(inf\) 以便赋值。

更新左右边界时要先递归到叶子结点再更新，因为每节点长度是从大到小的，而我们需要由小节点推大节点。

题目询问中为轮数，转化为层数需要在输入时减去 \(1\)。

Code：

#include<bits/stdc++.h>using namespace std;const int Ratio=0;
const int N=1e6+5;
const int maxx=2e9;
int n,m;
int v[N<<1],sl[N<<1],sr[N<<1],L[25],R[25];namespace Wisadel
{#define ls (rt<<1)#define rs (rt<<1|1)#define mid ((l+r)>>1)void Wbuild(int rt,int l,int r){if(l==r) return;int ceng=log2(r-l+1);// log2 自动向下取整 Wbuild(ls,l,mid),Wbuild(rs,mid+1,r);if(v[rt]==1) sl[rt]=sl[ls]+sl[rs]+1,sr[rt]=min(sr[ls],sr[rs]);else sl[rt]=min(sl[ls],sl[rs]),sr[rt]=sr[ls]+sr[rs]+1;// 判断节点类型并进行更新 L[ceng]=min(L[ceng],sl[rt]),R[ceng]=min(R[ceng],sr[rt]);// 更新每层范围 }short main(){scanf("%d%d",&n,&m);for(int i=1;i<=(1<<n)-1;i++) scanf("%d",&v[i]);for(int i=1;i<=n;i++) L[i]=maxx,R[i]=maxx;Wbuild(1,1,(1<<n));for(int i=1;i<=m;i++){int a,b;scanf("%d%d",&a,&b);b-=1;if(a>L[b]&&(1<<n)-a>=R[b]) printf("Yes\n");// 判断是否在范围内// (1<<n)-a>=R[b] 即为 (1<<n)-a+1>R[b] else printf("No\n");}return Ratio;}
}
int main(){return Wisadel::main();}

abc_362.C Sum=0

我在昨晚的 abc 中怒吃四发罚时，很好吃，你也来试试吧（雾

一道挺唐的题，感觉没啥技术含量，但就是不好 AC，问了一圈感觉我的方法还是比较正确的。

思路

输入时直接记录左右边界分别的和，判断是否存在。

若存在，则首先将答案序列赋为其值所在区间的中间值，求出 \(sum\)。然后遍历一遍 \(1\) ~ \(n\)，\(sum=0\) 时直接结束循环；若 \(sum>0\) 且 \(ans_i-l_i>=sum\)，那么直接将 \(ans_i\) 赋值为 \(ans_i-sum\) 然后退出循环即可，否则赋值为 \(l_i\) 并且 \(sum-=ans_i-l_i\)；若 \(sum<0\)，当 \(r_i-ans_i>=-sum\) 时，将 \(ans_i\) 赋值为 \(ans_i+(-sum)\)，否则赋值为 \(r_i\) 并且 \(sum+=r_i-ans_i\)。

方法的正确性可以证明。

Code：

#include<bits/stdc++.h>
#define fo(x,y,z) for(register int (x)=(y);(x)<=(z);(x)++)
using namespace std;
typedef long long ll;
#define lx int
inline lx qr()
{char ch=getchar();lx x=0,f=1;for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);return x*f;
}
#undef lx
#define qr qr()
const int Ratio=0;
const int N=1e6+5;
const int maxx=2e9;
int n;
ll ls,rs,l[N],r[N];
ll ans[N];
namespace Wisadel
{short main(){n=qr;fo(i,1,n) l[i]=qr,r[i]=qr,ls+=l[i],rs+=r[i];if(ls>0||rs<0) printf("No\n");else{printf("Yes\n");ll sum=0;fo(i,1,n){ans[i]=(l[i]+r[i])>>1;sum+=ans[i];}if(sum==0)fo(i,1,n) printf("%lld ",ans[i]);else {fo(i,1,n){if(sum>0&&ans[i]-l[i]>=sum){ans[i]-=sum;sum=0;break;}else if(sum>0&&ans[i]-l[i]<sum){sum-=ans[i]-l[i];ans[i]=l[i];}else if(sum<0&&r[i]-ans[i]>=-sum){ans[i]+=-sum;sum=0;break;}else if(sum<0&&r[i]-ans[i]<-sum){sum+=r[i]-ans[i];ans[i]=r[i];}}fo(i,1,n) printf("%lld ",ans[i]);}}return Ratio;}
}
int main(){return Wisadel::main();}

还是比较简单的，但丁真自己没过。

---

Updating。。。