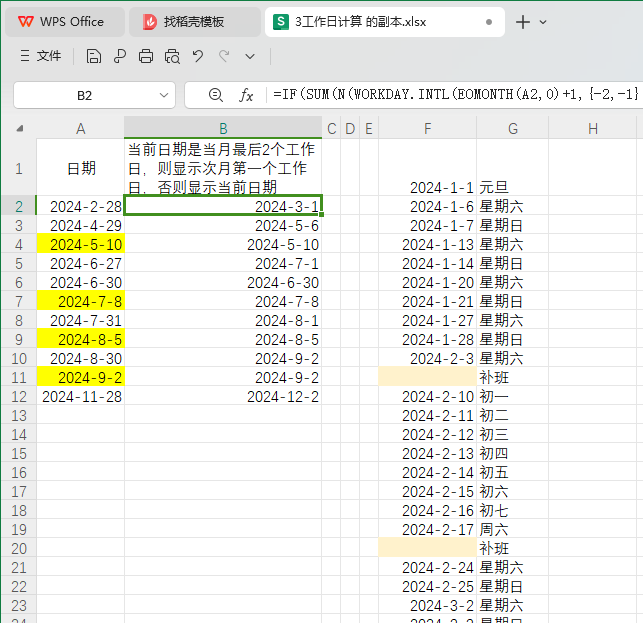
对于模糊的概念,如确定一个人是秃子吗,我们不能确认少于多少根头发的人是秃子,所以需要模糊综合评价法。
层次分析法
上一页层次分析法所求为各个影响因素的分立权重。那现在我们更进一步,通过之前利用层次分析法求得的权重来求出一个评价函数。
模型建立
根据之前所得影响因素建立代表综合评测的多种因素的因素集:
\(U = \{B_{11}, B_{12}, B_{13}, B_{21}, B_{22}, B_{23}, B_{31}, B_{32}, B_{41}, B_{42}, B_{51}, B_{52}\}\)
再建立多种决断构成的评判集合:
\(V = \{v_1, v_2, v_3, v_4, v_5\}\)
分别表示学习效率的评判标语为“优”,“良”,“中”,“可”,“差”,分别对应的在线学习效率程度为“很高” “高” “正常” “低” “很低” ,并规定评价集中各元素的量化值为 \(v_1=100,v_2=85,v_3=70,v_4=55,v_5=40\)。
然后根据在每个判断因素上,通过认为产品好坏的人数比例得到一个行向量,比如给电视图像方面打分的人数比例为50%,20%,20%,5%,5%,那么行向量为\([0.5\ 0.2\ 0.2\ 0.05\ 0.05]\)
如果有三个指标则可得到一个矩阵, 即为模糊评价矩阵。
以一个实际例子操作:
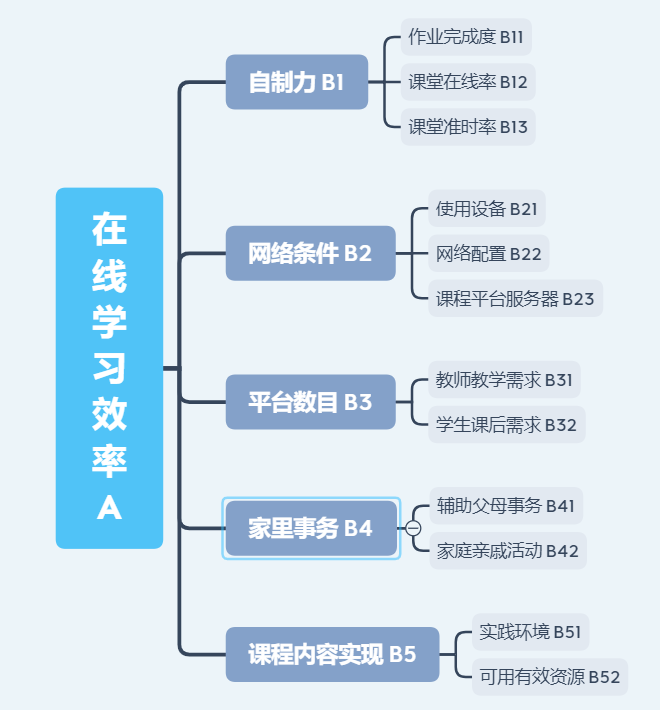
在图示的三层次结构综合评价指标体系中,\(B_1,B_2,B_3,B_4,B_5\) 分别表示不同的指标子集,具体含义如下:
- B1(自制力) = {B11, B12, B13} = {
- 作业完成度;
- 课堂在线率;课堂准时率
}
- B2(网络条件) = {B21, B22, B23} = {
- 使用设备;
- 网络配置;课程平台服务器
}
- B3(平台数目) = {B31, B32} = {
- 教师教学需求;
- 学生课后需求
}
- B4(家里事务) = {B41, B42} = {
- 辅助父母事务;
- 家庭亲戚活动
}
- B5(课程内容实现) = {B51, B52} = {
- 实践资源;
- 可用有效资源
}
对每个 \(B_i(i=1,2,3,4,5)\),分别进行模糊综合评测,单独考虑\(B_i(i=1,2,3,4,5)\)下的指标 \(B_{ij}\)
,通过德尔菲法得到隶属于 \(B_{ij}\)第 k个评语 \(v_k\)的程度,得到一份\(B_i(i=1,2,3,4,5)\)下的模糊评价矩阵 R:
对于每个大评价指标\(B_i\) , 得到子指标的权重集合w.
\(w\cdot R_i\)可得到\(B_i\)的模糊评价矩阵\(c_i\)
再用\(B_i\)的权重向量\(Q\cdot [c_1; \cdots ;c_n]\) 得到总的评价结果。
MATLAB代码
%%模糊评测法求在线学习效率
w1=[0.7584 0.1681 0.0735];%录入B1下的权重
w2=[0.0762 0.2308 0.6929];%录入B2下的权重
w3=[0.8000 0.2000];%B3下的权重
w4=[0.8333 0.1667];%B4下的权重
w5=[0.6667 0.3333];%B5下的权重
R1=[0.4 0.35 0.1 0.1 0.05; %R1模糊评价矩阵0.35 0.35 0.15 0.1 0.05;0.2 0.2 0.35 0.2 0.05];
R2=[0.4 0.25 0.25 0.05 0.05; %R2模糊评价矩阵0.35 0.3 0.25 0.05 0.05; 0.4 0.3 0.15 0.1 0.05];
R3=[0.3 0.2 0.3 0.1 0.1; %R3模糊评价矩阵0.4 0.3 0.15 0.1 0.05];
R4=[0.2 0.35 0.3 0.1 0.05; %R4模糊评价矩阵0.15 0.25 0.25 0.2 0.15];
R5=[0.35 0.2 0.2 0.15 0.1; %R5模糊评价矩阵0.3 0.25 0.25 0.15 0.05];
Q=[0.4803 0.302 0.0536 0.0787 0.0854];
%TR运算
C1=w1*R1;
C2=w2*R2;
C3=w3*R3;
C4=w4*R4;
C5=w5*R5;
E=Q*[C1;C2;C3;C4;C5]; %加入权重
fprintf('%.4f\n',E) %输出评语评价结果![[Unity] Dreamteck Splines实现沿路径移动功能](https://img2023.cnblogs.com/blog/2583637/202407/2583637-20240714165423885-405166439.gif)