SMU Summer 2024 Contest Round 4
Made Up
题意
给你三个序列 \(A,B,C\) ,问你满足 \(A_i = B_{C_j}\) 的 \((i,j)\) 对有多少。
思路
由于 \(1\le A_i,B_i,C_i\le N\) ,所以可以统计 \(Cnt[A_i]\) 和 \(Cnt[B_{C_i}]\) 的个数,两者相乘累加即可。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;vector<int> a(n), b(n), c(n);vector<i64> cnta(n + 1);for (auto &i : a) {cin >> i;cnta[i] ++;}for (auto &i : b)cin >> i;vector<i64> cntb(n + 1);for (auto &i : c) {cin >> i;cntb[b[--i]] ++;}i64 ans = 0;for (int i = 1; i <= n; i ++) {ans += cnta[i] * cntb[i];}cout << ans << '\n';return 0;
}H and V
题意
给你 \(H\times W\) 的只包含. 和#的矩阵, 你可以选择任意行任意列改成.,问你修改后使得矩阵中#的个数等于 k 的方案有多少种。
思路
因为 \(1\le H,W\le 6\),所以直接对边和列枚举改哪些行和列即可。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int h, w, k;cin >> h >> w >> k;vector<string> s(h);for (auto &i : s)cin >> i;auto calc = [](vector<string> ss) {int res = 0;for (auto i : ss)for (auto c : i)res += (c == '#');return res;};int ans = 0;for (int i = 0; i < (1 << h); i ++) {for (int j = 0; j < (1 << w); j ++) {auto S = s;for (int k = 0; k < h; k ++)if ((i >> k) & 1)S[k] = string(w, '.');for (int k = 0; k < w; k ++)if ((j >> k) & 1) {for (int p = 0; p < h; p ++)S[p][k] = '.';}if (calc(S) == k)ans ++;}}cout << ans << '\n';return 0;
}Moving Piece
题意
给你 n 个点,然后每个点 可以到达其他第 \(P_i\) 个点,到达下个点后可以获得对应的 \(C_i\) 分数,你可以选择某个点为起始点走 \(K\) 步,起始点的分数不计,问你最大能获得多少分。
思路
因为每个点只有一个方向,所以将它们抽象成图以后就是多个环,而你需要在这些环上找一个环走 \(K\) 步。
当走的步数大于环上的点数时,直接计算一下会经过多少次这个环,乘以环的总分数即可。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, k;cin >> n >> k;vector<int> p(n + 1);for (int i = 1; i <= n; i ++)cin >> p[i];vector<int> C(n + 1);for (int i = 1; i <= n; i ++)cin >> C[i];i64 ans = INT_MIN;for (int i = 1; i <= n; i ++) {i64 to = i, sum = 0;vector<i64> path;while (true) {to = p[to];sum += C[to];path.push_back(sum);if (to == i) break;}const int dis = path.size();for (int j = 0; j < dis && j < k; j ++) {int CircleNum = (k - 1 - j) / dis;ans = max(ans, path[j]);if(CircleNum > 0)ans = max(ans, path[j] + CircleNum * sum);}}cout << ans << '\n';return 0;
}Sum of Divisors
题意
设 \(f(X)\) 为 \(X\) 的所有因子数,求 \(\sum_{K=1}^NK\times f(K)\)。
思路
考虑一个数产生的贡献。
对于一个数,它只会在它的倍数中产生贡献,例如,2 只会在 \(2,4,6,8,10\dots\) 中产生贡献,而在上界为 \(N\) 的情况下只会有 \(\frac{N}{i}\) 个 \(i\) 的倍数,而对于 2 而言,它在 2 中产生的贡献为 2,在4 中的产生的贡献为 4,在 6 中产生的贡献为 6,\(\dots\),其他数同理,观察可得一个数产生的贡献为 \(i + 2i+3i+4i+\dots\),没错,这就是一个首项为 \(i\) ,公差为 \(i\),项数为 \(\frac{N}{i}\),末项为 \(\lfloor\frac{N}{i}\rfloor\times i\) 的等差数列,所以从 1 到 n 累加求和即可。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;i64 ans = 0;for(int i = 1;i <= n;i ++){i64 d = i, a1 = i, len = n / i, an = d * len;ans += len * (a1 + an) / 2;}cout << ans << '\n';return 0;
}Red and Green Apples
题意
给你三个序列 \(A,B,C\),\(C\) 序列中的任何数可以替换 \(A,B\) 中的任何数,你要选出 A 中 X 个,B 中 Y 个,求它们的和最大。
思路
将 A,B 排序后取前 X 个和前 Y 个放入 C 中,再将 C 排序,取出前 X+Y 个即可。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int x, y, a, b, c;cin >> x >> y >> a >> b >> c;vector<int> A(a), B(b), C(c);for (auto &i : A)cin >> i;for (auto &i : B)cin >> i;for (auto &i : C)cin >> i;sort(A.begin(), A.end(), greater<>());sort(B.begin(), B.end(), greater<>());for(int i = 0;i < x;i ++)C.push_back(A[i]);for(int i = 0;i < y;i ++)C.push_back(B[i]);sort(C.begin(),C.end(),greater<>());i64 ans = 0;for(int i = 0;i < x + y;i ++)ans += C[i];cout << ans << '\n';return 0;
}Rem of Sum is Num
题意
给你序列 A,求 A 中连续子序列之和模 K 后等于该子序列中元素数量的连续子序列数量。
思路
转化题意,即求:
复杂度\(O(n^3)\),显然超时。
考虑优化,前缀和优化即:
至此,这道题就变成了求区间长度最大为 k 的 满足以上条件的方案数,在模 k 后其区间元素数量最多为 k ,否则就不满足条件,超过区间长度需减掉。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);i64 n, k;cin >> n >> k;vector<i64> a(n + 1), pre(n + 1);for (int i = 1; i <= n; i ++) {cin >> a[i];pre[i] = pre[i - 1] + a[i];}for (int i = 1; i <= n; i ++) {pre[i] = (pre[i] - i) % k;}i64 ans = 0;int len = min(k-1, n);map<i64, i64> mp;for (int i = 0; i <= n; i ++) {if (i > len) mp[pre[i - k]]--;ans += mp[pre[i]];mp[pre[i]] ++;}cout << ans << '\n';return 0;
}Keep Connect
题意
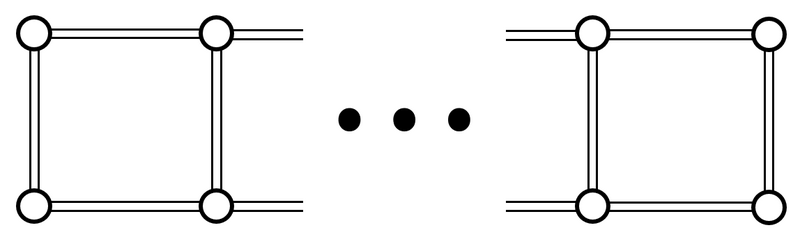
给定 $ n, p $,存在如图的 $ 2 \times n $ 的网格图,显然初始共有 $ 2n $ 个顶点和 $ 3n - 2 $ 条边,分别求删除 $ i \in [1, n - 1] $ 条边后仍使图连通的删边方案数,对 $ p $ 取模。
思路
将上下的两个点看成一列,考虑 dp。
设 \(dp_{i,j,0/1}\) 为前 i 列中删掉 j 条边是否连通的方案数。
首先假设第 i 列连通:
-
那么会有四种情况使得第 i+1 列连通:
-
前三种:
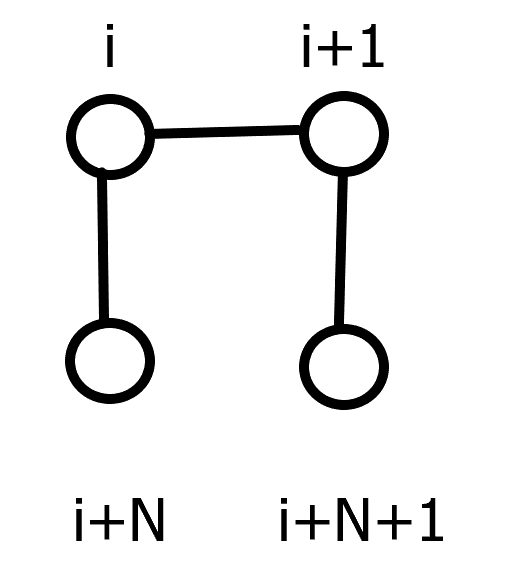
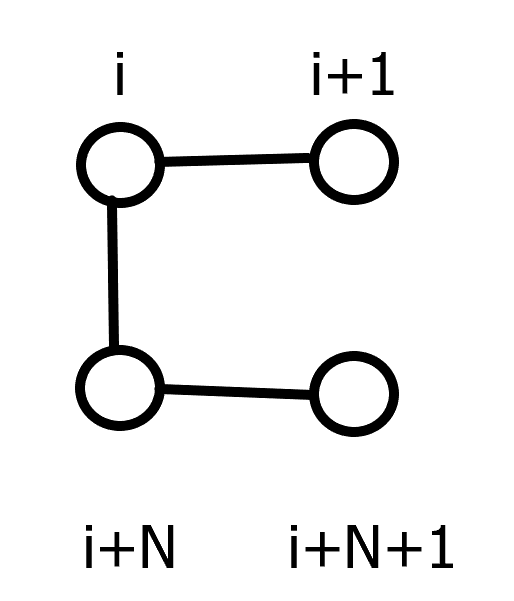
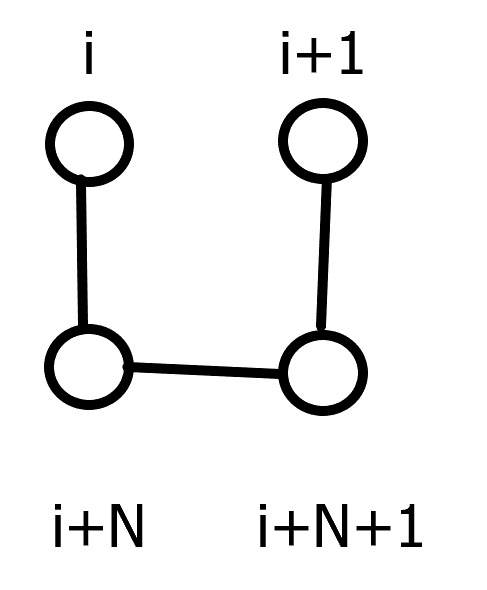
得出转移方程为 \(dp_{i+1,j+1,1} += dp_{i,j,1}\times 3\) -
第四种:
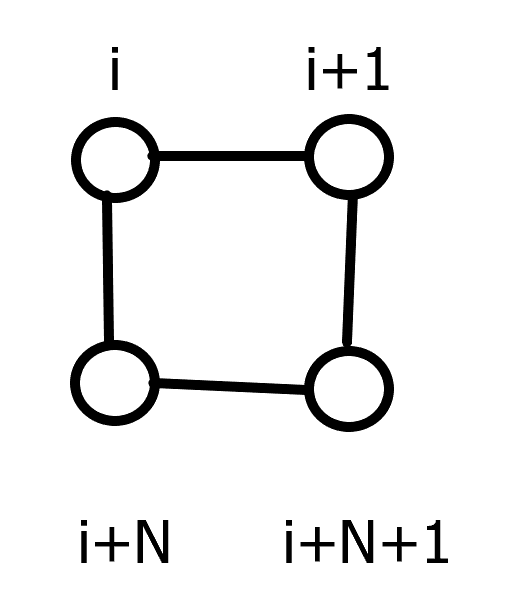
得出转移方程为 \(dp_{i+1,j,1}+=dp_{i,j,1}\)
-
-
会有两种情况使得第 i+1 列无法连通:
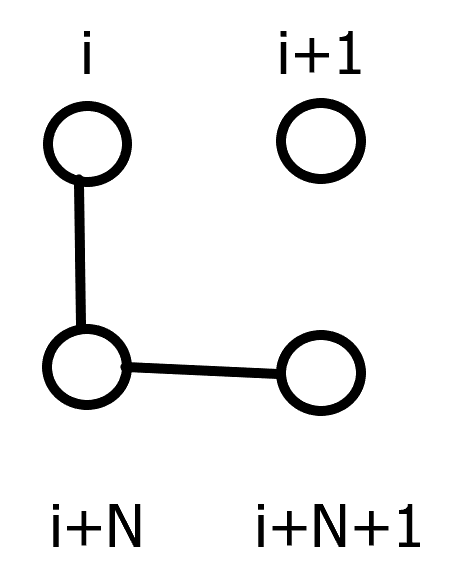
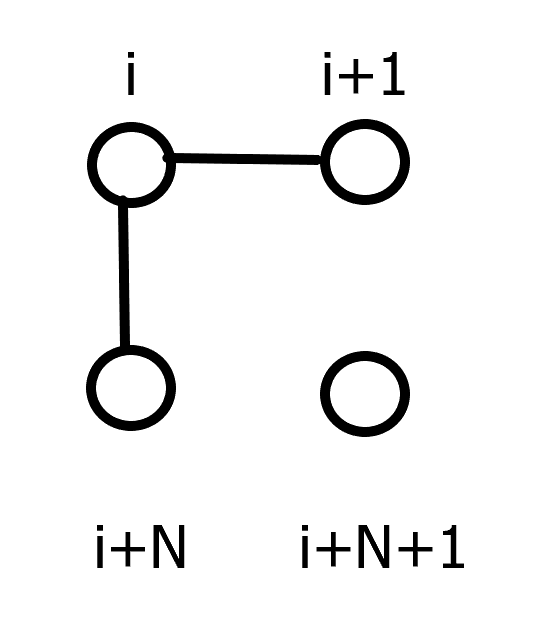
得出转移方程为 \(dp_{i+1,j+2,0}+=dp_{i,j,1}\times 2\)
假设第 i 列不连通:
-
使得第 i+1 列连通:
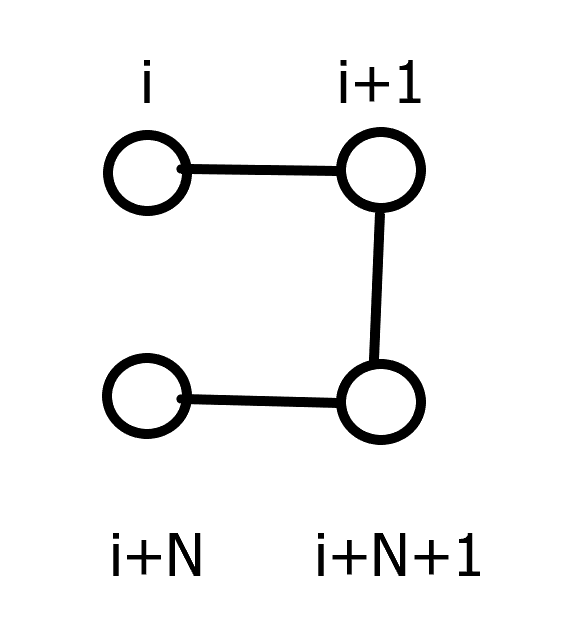
得出转移方程为 \(dp_{i+1,j,1}+=dp_{i,j,0}\)
-
使得第 i+1 列不连通:
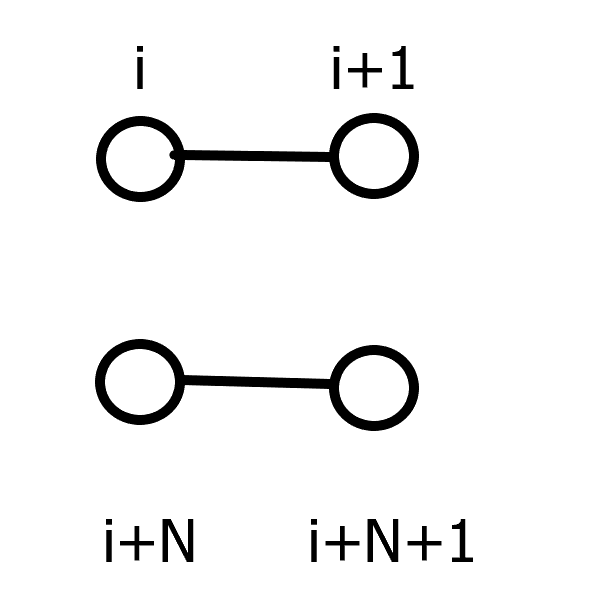
得出转移方程为 \(dp_{i+1,j+1,0}+=dp_{i,j,0}\)
另外还有些减去三边的情况,但是那种情况产生后后面都不可能再连通,对答案无贡献。
代码
#include<bits/stdc++.h>using namespace std;using i64 = long long;const int N = 3e3 + 10;
i64 dp[N][N][2];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);i64 n, p;cin >> n >> p;dp[1][0][1] = dp[1][1][0] = 1;for (int i = 1; i <= n; i ++) {for (int j = 0; j < n; j ++) {dp[i + 1][j + 1][1] = (dp[i + 1][j + 1][1] + dp[i][j][1] * 3) % p;dp[i + 1][j][1] = (dp[i + 1][j][1] + dp[i][j][1]) % p;dp[i + 1][j + 2][0] = (dp[i + 1][j + 2][0] + dp[i][j][1] * 2) % p;dp[i + 1][j][1] = (dp[i + 1][j][1] + dp[i][j][0]) % p;dp[i + 1][j + 1][0] = (dp[i + 1][j + 1][0] + dp[i][j][0]) % p;}}for (int i = 1; i < n; i ++)cout << dp[n][i][1] << " \n"[i == n - 1];return 0;
}