Splay 树, 或 伸展树,是一种平衡二叉查找树,它通过 Splay/伸展操作 不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,能够在均摊 O(\log N) 时间内完成插入,查找和删除操作,并且保持平衡而不至于退化为链。
Splay 树由 Daniel Sleator 和 Robert Tarjan 于 1985 年发明。
code:
using namespace std;
const int maxn = 1e5+10;
int root,tot,fa[maxn],ch[maxn][2],val[maxn],cnt[maxn],sz[maxn];
int rt;
struct Splay{void maintain(int x){sz[x] = sz[ch[x][0]]+sz[ch[x][1]]+cnt[x];//在改变节点位置后,将节点x的size更新 }bool get(int x){//判断x是父节点的左儿子还是右儿子 return x == ch[fa[x]][1];}void clear(int x){//销毁节点x ch[x][0] = ch[x][1] = fa[x] = val[x] = sz[x] = cnt[x] = 0;}/*将 y 的左儿子指向 x 的右儿子,且 x 的右儿子(如果 x 有右儿子的话)的父亲指向 y;ch[y][0]=ch[x][1]; fa[ch[x][1]]=y;将 x 的右儿子指向 y,且 y 的父亲指向 x;ch[x][chk^1]=y; fa[y]=x;若原来的 y 还有父亲 z,那么把 z 的某个儿子(原来 y 所在的儿子位置)指向 x,且 x 的父亲指向 z。fa[x]=z; if(z) ch[z][y==ch[z][1]]=x;*/ void rotate(int x){int y = fa[x],z = fa[y],chk = get(x);ch[y][chk] = ch[x][chk^1];if(ch[x][chk^1]) fa[ch[x][chk^1]] = y;ch[x][chk^1] = y;fa[y] = x;fa[x] = z;if(z) ch[z][y == ch[z][1]] = x;maintain(y);maintain(x); }/*Splay 操作规定:每访问一个节点 x 后都要强制将其旋转到根节点。Splay 操作即对 x 做一系列的 splay 步骤。每次对 x 做一次 splay 步骤,x 到根节点的距离都会更近。定义 p 为 x 的父节点。Splay 步骤有三种,具体分为六种情况:*/void splay(int x){for(int f = fa[x];f = fa[x],f;rotate(x)){if(fa[f]) rotate(get(x) == get(f)?f:x);}rt = x;}/*如果树空了,则直接插入根并退出。如果当前节点的权值等于 k 则增加当前节点的大小并更新节点和父亲的信息,将当前节点进行 Splay 操作。否则按照二叉查找树的性质向下找,找到空节点就插入即可(请不要忘记 Splay 操作)。*/void ins(int k){if(!rt){val[++tot] = k;cnt[tot]++;rt = tot;maintain(rt);return;}int cur = rt,f = 0;while(1){if(val[cur] == k){cnt[cur]++;maintain(cur);maintain(f);splay(cur);break;}f = cur;cur = ch[cur][val[cur]<k];if(!cur){val[++tot] = k;cnt[tot]++;fa[tot] = f;ch[f][val[f]<k] = tot;maintain(f);maintain(tot);splay(tot);break;}}}/*如果 x 比当前节点的权值小,向其左子树查找。如果 x 比当前节点的权值大,将答案加上左子树(size)和当前节点(cnt)的大小,向其右子树查找。如果 x 与当前节点的权值相同,将答案加 1 并返回。*/int rk(int k){int res = 0,cur = rt;while(1){if(k < val[cur]){cur = ch[cur][0];}else{res += sz[ch[cur][0]];if(!cur) return res+1;if(k == val[cur]){splay(cur);return res+1;}res += cnt[cur];cur = ch[cur][1];}}}/*如果左子树非空且剩余排名 k 不大于左子树的大小 size,那么向左子树查找。否则将 k 减去左子树的和根的大小。如果此时 k 的值小于等于 0,则返回根节点的权值,否则继续向右子树查找。*/int kth(int k) {int cur = rt;while (1) {if (ch[cur][0] && k <= sz[ch[cur][0]]) {cur = ch[cur][0];} else {k -= cnt[cur] + sz[ch[cur][0]];if (k <= 0) {splay(cur);return val[cur];}cur = ch[cur][1];}}}/*前驱定义为小于 x 的最大的数,那么查询前驱可以转化为:将 x 插入(此时 x 已经在根的位置了),前驱即为 x 的左子树中最右边的节点,最后将 x 删除即可。*/int pre(){int cur = ch[rt][0];if(!cur) return cur;while(ch[cur][1]) cur = ch[cur][1];splay(cur);return cur;}int nex(){//后继 int cur = ch[rt][1];if (!cur) return cur;while(ch[cur][0]) cur = ch[cur][0];splay(cur);return cur;}/*首先将 x 旋转到根的位置。如果 cnt[x]>1(有不止一个 x),那么将 cnt[x] 减 1 并退出。
否则,合并它的左右两棵子树即可。合并:
如果 x 和 y 其中之一或两者都为空树,直接返回不为空的那一棵树的根节点或空树。
否则将 x 树中的最大值 \operatorname{Splay} 到根,然后把它的右子树设置为 y 并
更新节点的信息,然后返回这个节点。
*/void del(int k) {rk(k);if (cnt[rt] > 1) {cnt[rt]--;maintain(rt);return;}if (!ch[rt][0] && !ch[rt][1]) {clear(rt);rt = 0;return;}if (!ch[rt][0]) {int cur = rt;rt = ch[rt][1];fa[rt] = 0;clear(cur);return;}if (!ch[rt][1]) {int cur = rt;rt = ch[rt][0];fa[rt] = 0;clear(cur);return;}int cur = rt;int x = pre();fa[ch[cur][1]] = x;ch[x][1] = ch[cur][1];clear(cur);maintain(rt);}}tree;
int n;
int main(){cin>>n;while(n--){int opt,x;cin>>opt>>x;if (opt == 1)tree.ins(x);else if (opt == 2)tree.del(x);else if (opt == 3)printf("%d\n", tree.rk(x));else if (opt == 4)printf("%d\n", tree.kth(x));else if (opt == 5)tree.ins(x), printf("%d\n", val[tree.pre()]), tree.del(x);elsetree.ins(x), printf("%d\n", val[tree.nex()]), tree.del(x);}return 0;
}
旋转操作
为了使 Splay 保持平衡而进行旋转操作,旋转的本质是将某个节点上移一个位置。
旋转需要保证:
整棵 Splay 的中序遍历不变(不能破坏二叉查找树的性质)。
受影响的节点维护的信息依然正确有效。
root 必须指向旋转后的根节点。
在 Splay 中旋转分为两种:左旋和右旋。
过程
具体分析旋转步骤(假设需要旋转的节点为 x,其父亲为 y,以右旋为例)
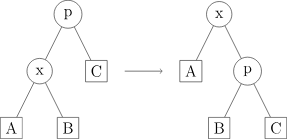
将 y 的左儿子指向 x 的右儿子,且 x 的右儿子(如果 x 有右儿子的话)的父亲指向 y;ch[y][0]=ch[x][1]; fa[ch[x][1]]=y;
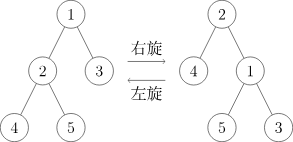
将 x 的右儿子指向 y,且 y 的父亲指向 x;ch[x][chk^1]=y; fa[y]=x;
如果原来的 y 还有父亲 z,那么把 z 的某个儿子(原来 y 所在的儿子位置)指向 x,且 x 的父亲指向 z。fa[x]=z; if(z) ch[z][y==ch[z][1]]=x;
Splay 操作
Splay 操作规定:每访问一个节点 x 后都要强制将其旋转到根节点。
Splay 操作即对 x 做一系列的 splay 步骤。每次对 x 做一次 splay 步骤,x 到根节点的距离都会更近。定义 p 为 x 的父节点。Splay 步骤有三种,具体分为六种情况:
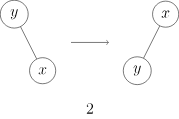
zig: 在 p 是根节点时操作。Splay 树会根据 x 和 p 间的边旋转。zig 存在是用于处理奇偶校验问题,仅当 x 在 splay 操作开始时具有奇数深度时作为 splay 操作的最后一步执行。
splay-zig
即直接将 x 左旋或右旋(图 1, 2)
图 1

图 2
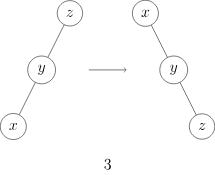
zig-zig: 在 p 不是根节点且 x 和 p 都是右侧子节点或都是左侧子节点时操作。下方例图显示了 x 和 p 都是左侧子节点时的情况。Splay 树首先按照连接 p 与其父节点 g 边旋转,然后按照连接 x 和 p 的边旋转。
splay-zig-zig
即首先将 g 左旋或右旋,然后将 x 右旋或左旋(图 3, 4)。
图 3
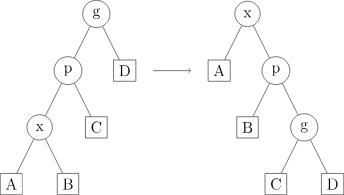
图 4
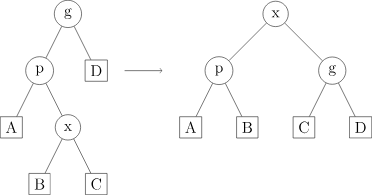
zig-zag: 在 p 不是根节点且 x 和 p 一个是右侧子节点一个是左侧子节点时操作。Splay 树首先按 p 和 x 之间的边旋转,然后按 x 和 g 新生成的结果边旋转。
splay-zig-zag
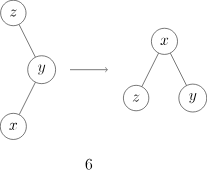
即将 x 先左旋再右旋、或先右旋再左旋(图 5, 6)。
图 5
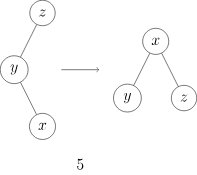
图 6