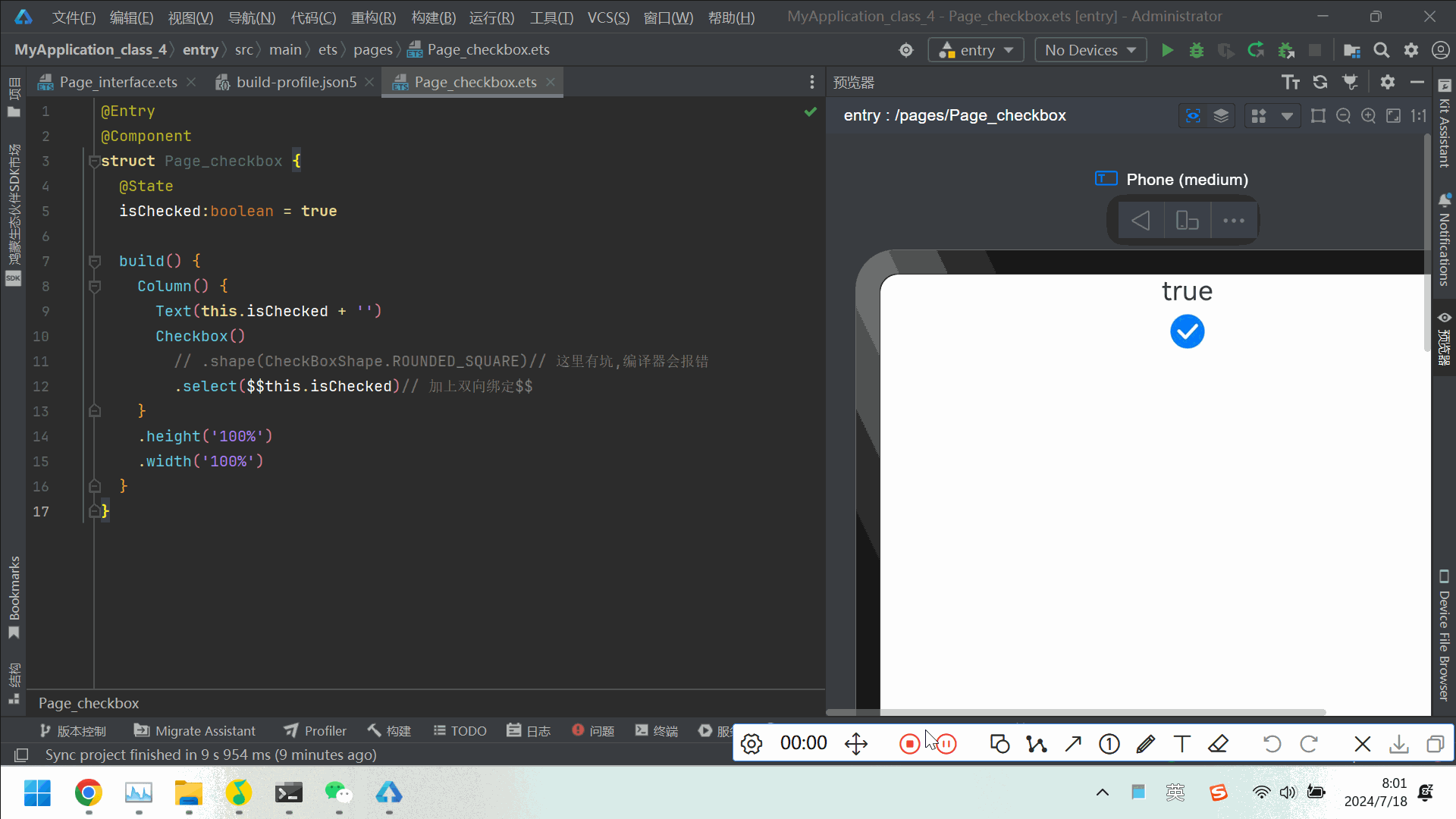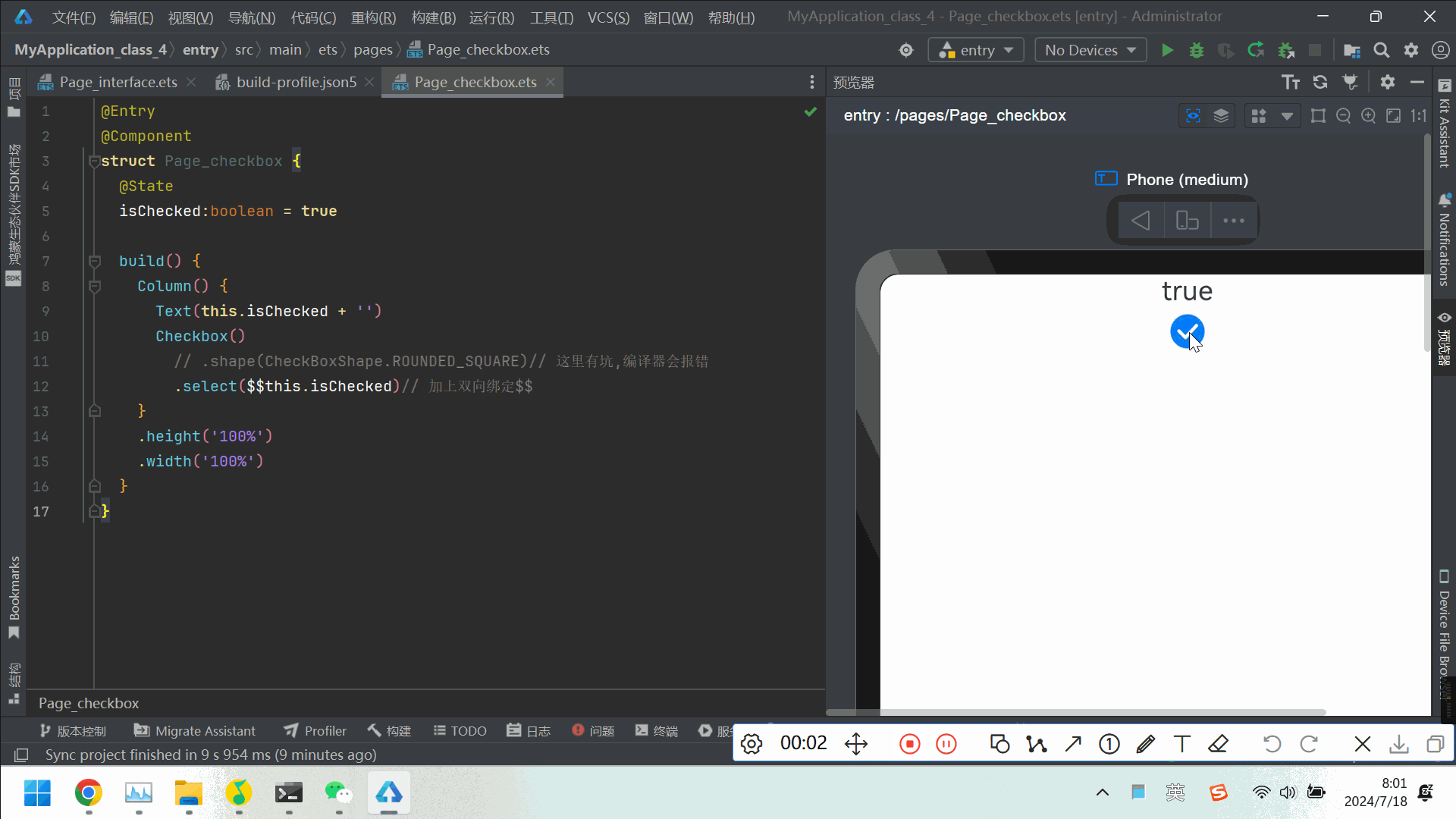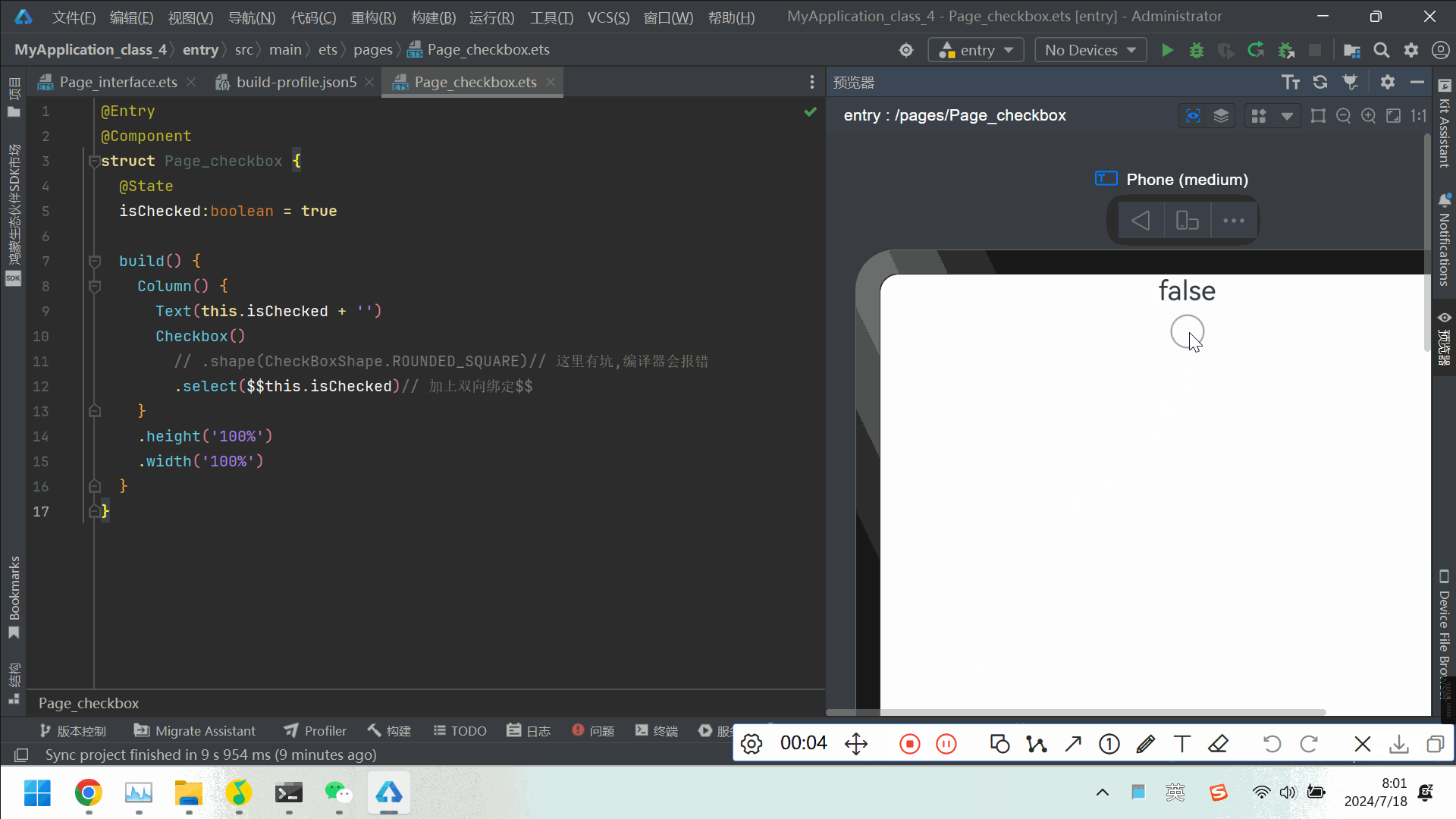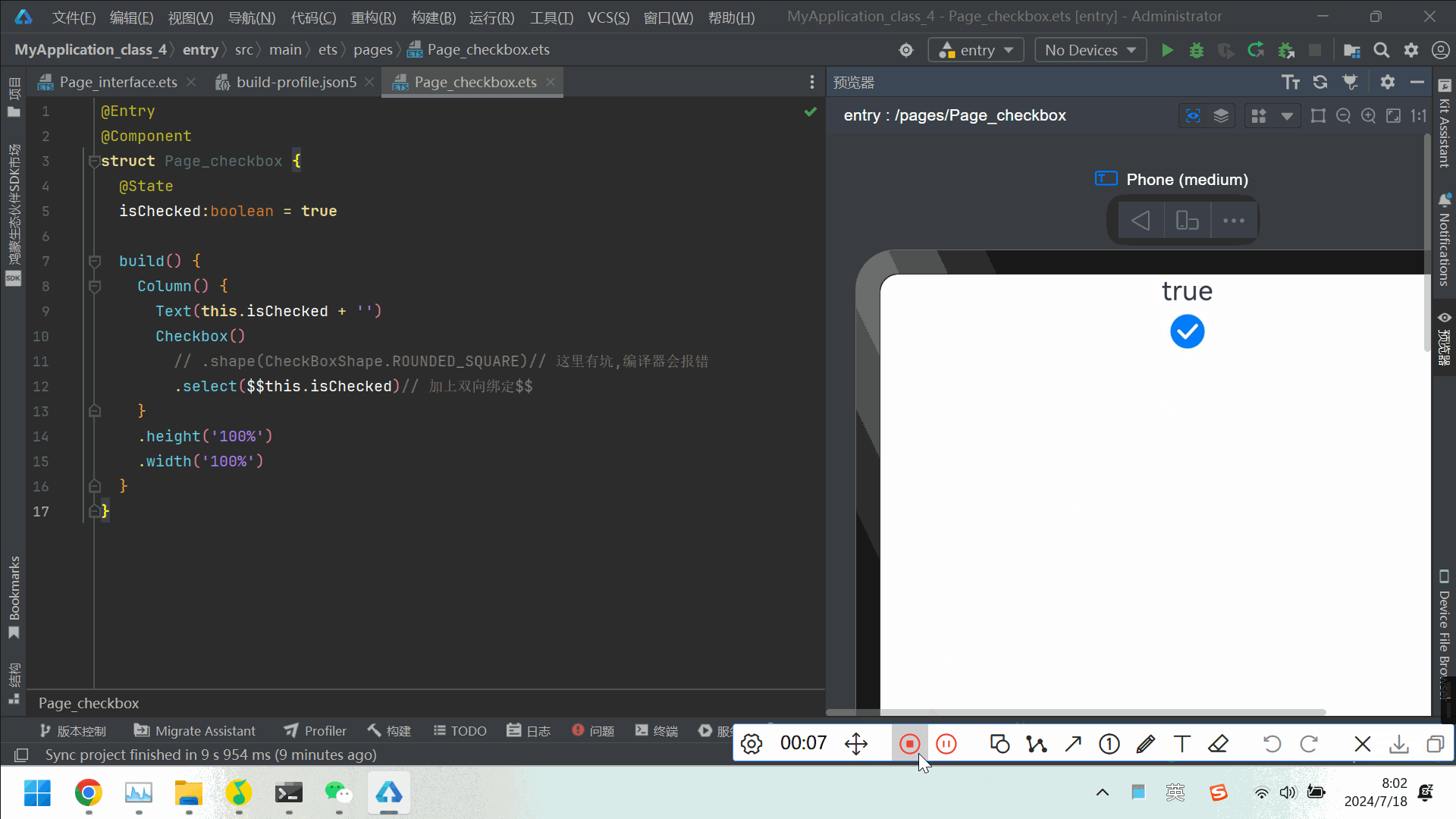
小蓝的二进制询问
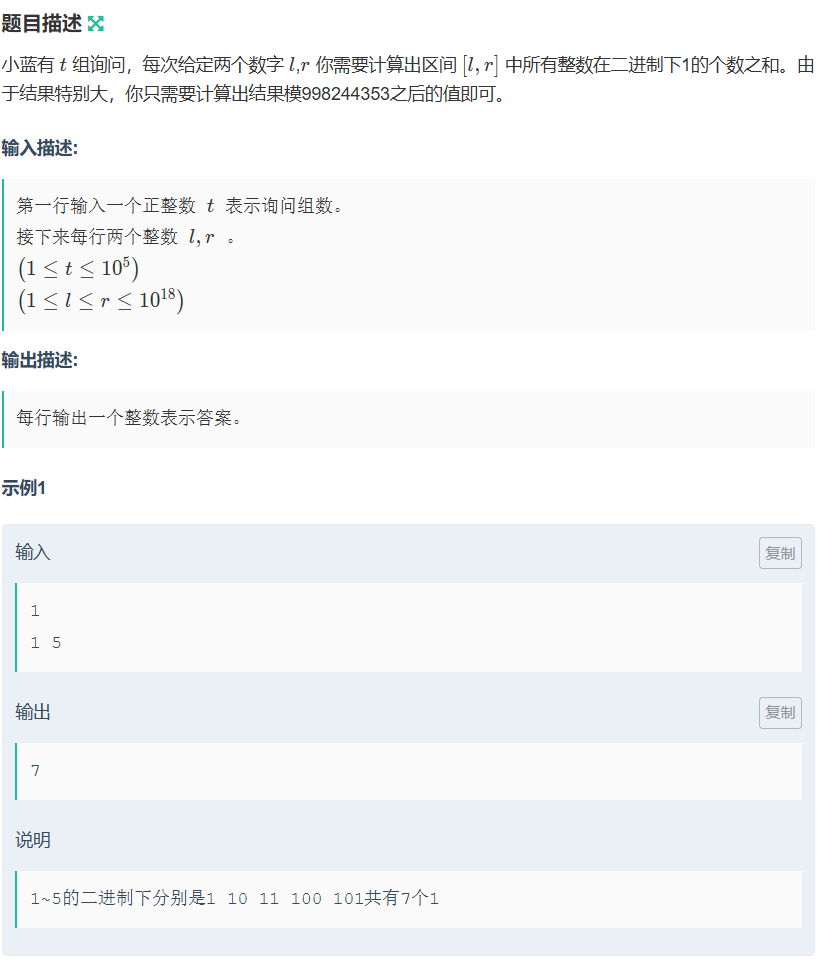
找规律,可以发现 把从0开始的十进制数字转化为二进制。每一个二进制位有0或1两种状态。从低到高的第一位以2为周期,第二位以4为周期,第三位以8为周期……也就是说第n位以 2^{n} 为周期。每个周期都是前一半是0,后一半是1 。
举例:
000 001 010 011 100 ……
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=100;
long long f[N][N];
int a[N];
int k;
int mod = 998244353;
int c;
int ans = 0;
int get(int x) //计算x的二进制长度
{int cnt = 0;while(x){x/=2;cnt++;}return cnt;
}
int solve(long long x)
{ans = 0 ;int cnt = get(x);x++; //因为周期是从0开始算的for(int i=1;i<=cnt;i++){int tt = pow(2,i); //第i位的周期ans += (x/tt)*(tt/2); //0~x 第i位1的个数ans %= mod;ans += max(0ll,x%tt-tt/2); //周期内仔细判断ans %= mod;}return ans;
}signed main()
{int t, l, r;cin >> t;while(t--){cin >> l >> r;int ans = (solve(r) - solve(l-1)+mod) % mod; //差分求区间cout << ans << endl;}return 0;
}
旅途的终点
注意!是按既定的路线旅游的!所以不能简单地通过排序找出k个最大的点。
正解:维护一个元素从小到大的大小为k的优先队列,从1~n按顺序放入数。当队列满时,从队首弹出最小的元素,放入接下来的元素。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define int ll
typedef pair<int,int> PII;
typedef unsigned long long ull;
const int ddx[8]={-1, 0, 1, 0, 1, -1, 1, -1};
const int ddy[8]={0, 1, 0, -1, -1, 1, 1, -1};
const int INF=0x3f3f3f3f;
const int N=6e5+10;
int n,m,k;
int a[N];
int sum = 0;
void solve()
{cin>>n>>m>>k;for(int i=1;i<=n;i++) cin>>a[i];priority_queue<int,vector<int>,greater<int>>q;for(int i=1;i<=n;i++){q.push(a[i]);if(q.size()>k){sum+=q.top();q.pop();}if(sum>=m){cout<<i-1<<endl;return;}}cout<<n<<endl;return;
}
signed main() {ios::sync_with_stdio(0);cin.tie(0);int t=1;//cin >> t;while(t--) {solve();}return 0;
}