1--栈的压入、弹出序列（31）

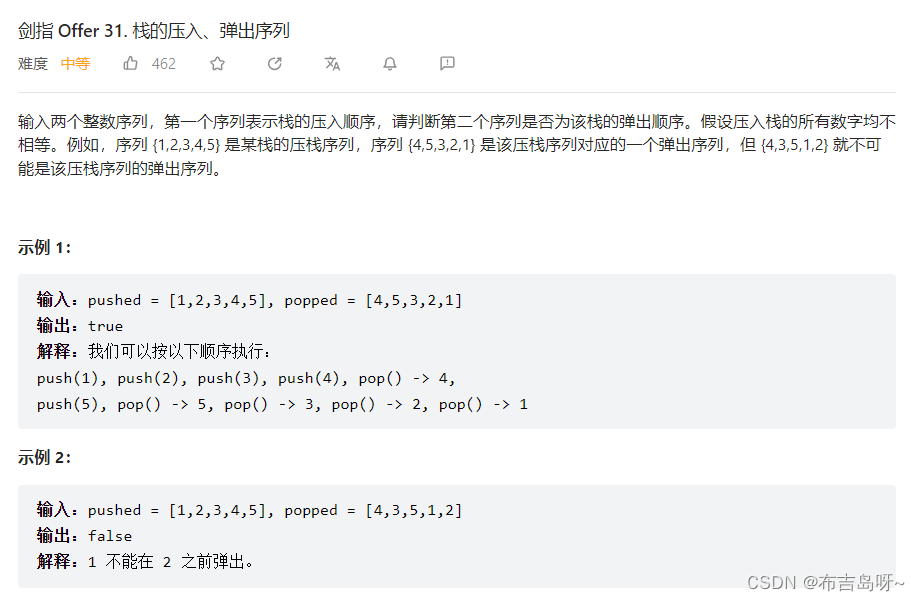
直观思路：用两个指针 i 和 j 指向压入和弹出的 vector，终止条件是：所有元素都压入了辅助栈（i > len），且辅助栈当前的栈顶元素与弹出的元素 popped[j] 不相等；

#include <iostream>
#include <vector>
#include <stack>class Solution {
public:bool validateStackSequences(std::vector<int>& pushed, std::vector<int>& popped) {int len = pushed.size();if (len == 0) return true;int i = 0, j = 0; // i 指向 pushed 的元素，j 指向 popped 的元素while(i < len || !st.empty()){if (i >= len && st.top() != popped[j]){ // 栈顶元素不等于当前要pop的元素，且已push完所有元素return false;}if (!st.empty() && st.top() == popped[j]){ // 如果栈顶元素等于当前要pop的元素，pop出栈顶元素，j下移st.pop();j++;}else if(i < len && pushed[i] != popped[j]){ // i 指向的元素不等于 j 指向的元素，将 i 压入堆栈中st.push(pushed[i]);i++;}else if(i < len && pushed[i] == popped[j]){ // i 指向的元素等于 j 指向的元素，i，j移向下一位i++;j++;}}return true;}private:std::stack<int> st;
};int main(int argc, char *argv[]){std::vector<int> push = {2, 1, 0};std::vector<int> pop = {1, 2, 0};Solution S1;bool res = S1.validateStackSequences(push, pop);if(res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}

简便思路：

        模拟栈的压入顺序，依次压入 pushed 里的所有元素，用一个指针 j 指向需要弹出的元素，当符合弹出要求时就弹出对应的元素；

        当辅助栈为空时，表明需要弹出的元素都顺利弹出，返回 true；

#include <iostream>
#include <vector>
#include <stack>class Solution {
public:bool validateStackSequences(std::vector<int>& pushed, std::vector<int>& popped) {std::stack<int> st;int n = pushed.size();for (int i = 0, j = 0; i < n; i++) {st.emplace(pushed[i]); while (!st.empty() && st.top() == popped[j]) { // 符合弹出要求，直接 pop 出栈顶元素st.pop();j++;}}return st.empty(); // 所有元素都顺利pop出，返回true;}
};int main(int argc, char *argv[]){std::vector<int> push = {2, 1, 0};std::vector<int> pop = {1, 2, 0};Solution S1;bool res = S1.validateStackSequences(push, pop);if(res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}

2--从上到下打印二叉树（32）

主要思路：层次遍历打印二叉树结点

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};class Solution {
public:std::vector<int> levelOrder(TreeNode* root) {if (root == NULL) return Res;Q1.push(root);while(!Q1.empty()){temp = Q1.front();Q1.pop();Res.push_back(temp->val);if(temp->left != NULL){Q1.push(temp->left);}if(temp->right != NULL){Q1.push(temp->right);}}return Res;}private:std::queue<TreeNode *> Q1;std::vector<int> Res;TreeNode *temp;
};int main(int argc, char *argv[]){TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution s1;std::vector<int> res = s1.levelOrder(Node1);for(int item : res){std::cout << item << " ";}return 0;
}

3--从上到下打印二叉树II（32）

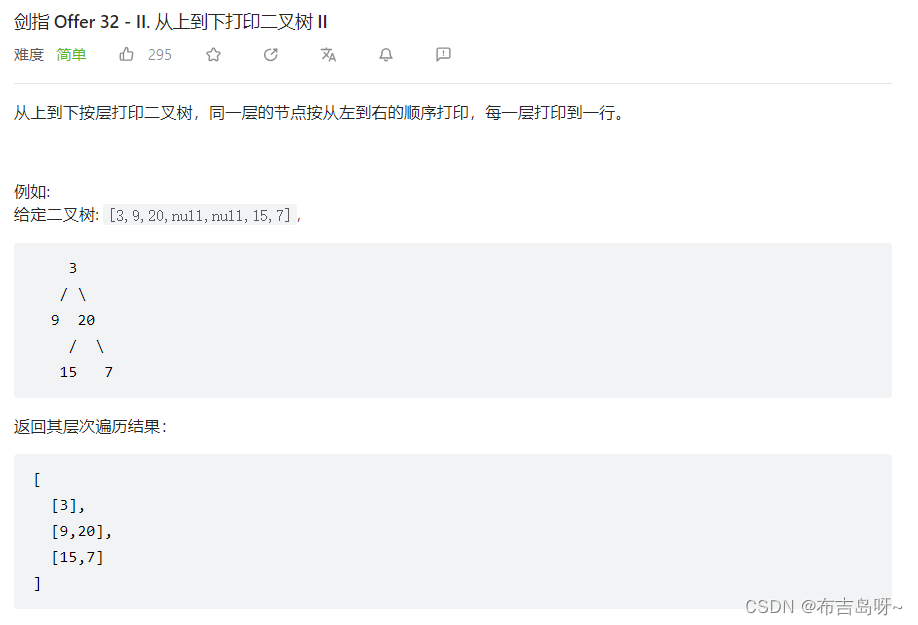
主要思路：

        与上题类似，借助于层次遍历，不同的是为了打印每一层的结点，需要循环当前层的结点数次，每一次当前队列的结点数实质上等于当前层的结点数，因此只需要循环队列的长度次，并记录对应的结点值即可；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};class Solution {
public:std::vector<std::vector<int>> levelOrder(TreeNode* root) {if(root == NULL) return Res;Q1.push(root);while(!Q1.empty()){int num = Q1.size(); // 当前层的结点数for(int i = 0; i < num; i++){temp_node = Q1.front();Q1.pop();temp.push_back(temp_node->val);if(temp_node->left != NULL) Q1.push(temp_node->left); if(temp_node->right != NULL) Q1.push(temp_node->right);}    Res.push_back(temp);temp.clear();}return Res;}
private:std::vector<std::vector<int>> Res;std::queue<TreeNode *> Q1;std::vector<int> temp;TreeNode * temp_node;
};int main(int argc, char *argv[]){TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution s1;std::vector<std::vector<int>> res = s1.levelOrder(Node1);for(int i = 0; i < res.size(); i++){for(int item : res[i]){std::cout << item << " ";}std::cout << std::endl;}return 0;
}

4--从上到下打印二叉树III（32）

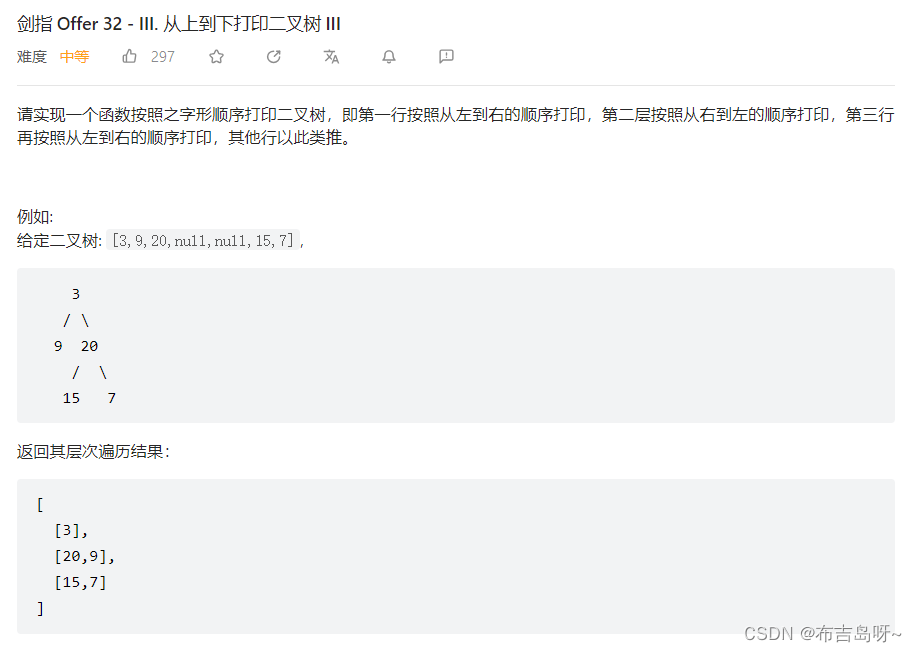
主要思路：