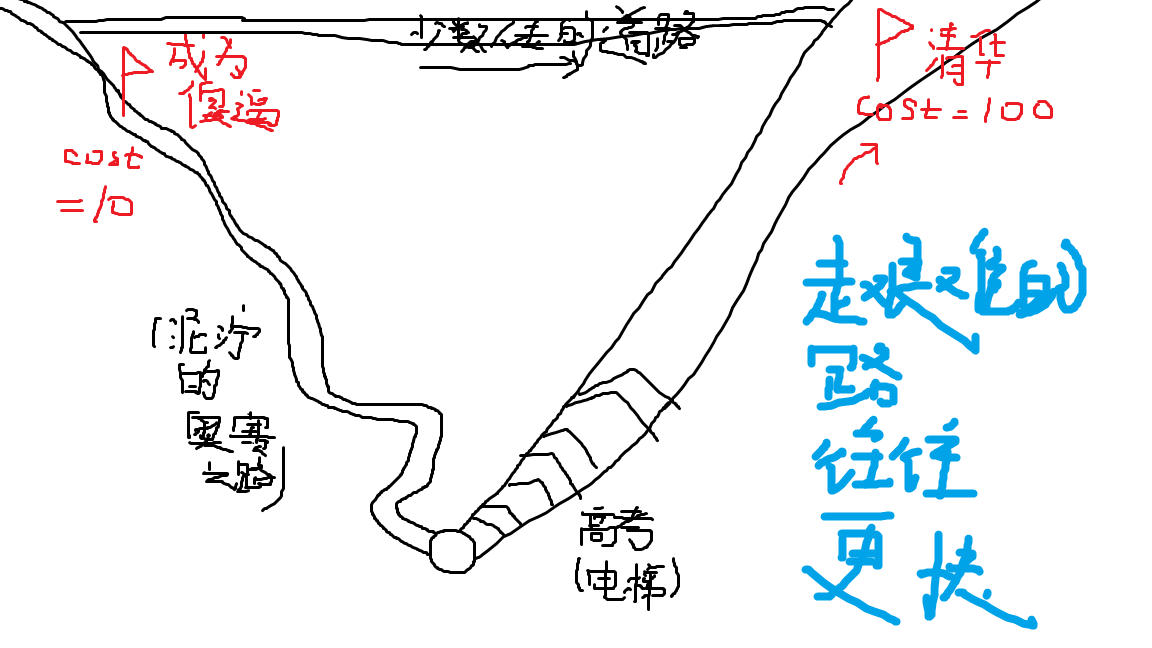
int id(int l,int r) {return (l+r)|(l!=r);} //代码1
证明思路:引导并说明某种做法发生冲突的情况,并证明修改后不会发生冲突
首先让我们考虑如果为
int id(int l,int r) {return (l+r);} //代码2
会出现什么冲突,如图
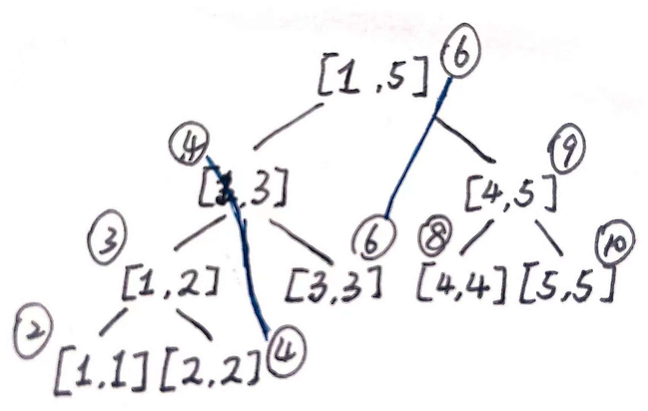
此时 [1,3] 与 [2,2] ,[1,5] 与 [3,3] 冲突
结论1:线段树中序遍历节点l+r单调不降,且节点u只在长度为奇数时会与左儿子右链端点的l+r相同
显然对于每一个节点u,\(l_{lson}+r_{lson}<l_u+r_u<l_{rson}+r_{rson}\)
因此我们只需要证明任意节点u大于等于其左儿子的右链终点
当 \(r_u-l_u+1\) 为奇数,则左儿子右链端点为 \((l_u+r_u)/2\),结论成立
当 \(r_u-l_u+1\) 为偶数,则左儿子右链端点为 \((l_u+r_u-1)/2\),结论成立
结论2: \(l_u+r_u\) 小于右儿子左链终点
与结论1证法相同
结论3:叶结点 \(l_u+r_u\) 为偶数
由结论1,只有节点u在长度为奇数时会与左儿子右链终点冲突。
由结论2,节点u不会与右子树冲突。
此时我们选择对于非叶结点长度为奇数的点,将其编号加1。(冲突解决措施,即代码1)
由结论2,3,因为长度为奇数的节点l+r为偶数,叶结点与其不同且也为偶数,因此将父节点加1后,与右儿子左链终点仍不冲突。
因此该编号方式正确。