因子分析法————数据降维

因子分析法通过研究变量间的相关系数矩阵，把这些变量间错综复杂的关系归结成少数几个综合因子，起到了很好的降维作用

目录

• 一、因子分析与主成分分析的对比
  • 1.原理对比
  • 2.作用区别
• 二、因子分析的实例
• 三、因子分析的理论介绍
  • 1.因子分析的模型
  • 2.模型假设
  • 3.因子载荷矩阵的统计意义
    • （1）A的行元素平方和
    • （2）A的列元素平方和
  • 4.参数估计
  • 5.因子旋转的方法
  • 6.因子得分
• 四、因子分析的操作步骤
• 五、结果分析
  • 1.模型检验
    • （1）KMO检验和巴特利特球形检验。
    • （2）巴特利特球形检验
  • 2.确定因子的数目
  • 3.调整因子个数重新计算
  • 4.公因子方差
  • 5.总方差解释表
    • （1）初始特征值
    • （2）载荷平方和
  • 6.成分矩阵
  • 7.旋转后的因子载荷散点图
  • 8.因子得分

一、因子分析与主成分分析的对比

1.原理对比

主成分分析的原理是把主成分分解为原始指标数据的线性组合
而因子分析则是找出原始指标数据的公共因子

2.作用区别

二、因子分析的实例

我们要对某个事物进行评价，由于评价指标太多，往往很难做出正确的评价，此时就需要对指标进行降维处理

三、因子分析的理论介绍

1.因子分析的模型

将原始指标分解为公共因子，特殊因子的线性组合。然后写出其矩阵形式，我们的目标就是解出因子载荷矩阵A

2.模型假设

此处假设的目的是保证公共因子之间不相关

3.因子载荷矩阵的统计意义

（1）A的行元素平方和

A的行元素平方和hi表示原始变量z,对公因子依赖的程度

（2）A的列元素平方和

4.参数估计

参数估计就是解因子载荷矩阵A，SPSS中提供了很多中方法，其中最常用的有三种，在下图中已经用红色标出。
在应用中我们可以三个都试一下，找出最好解释的一种

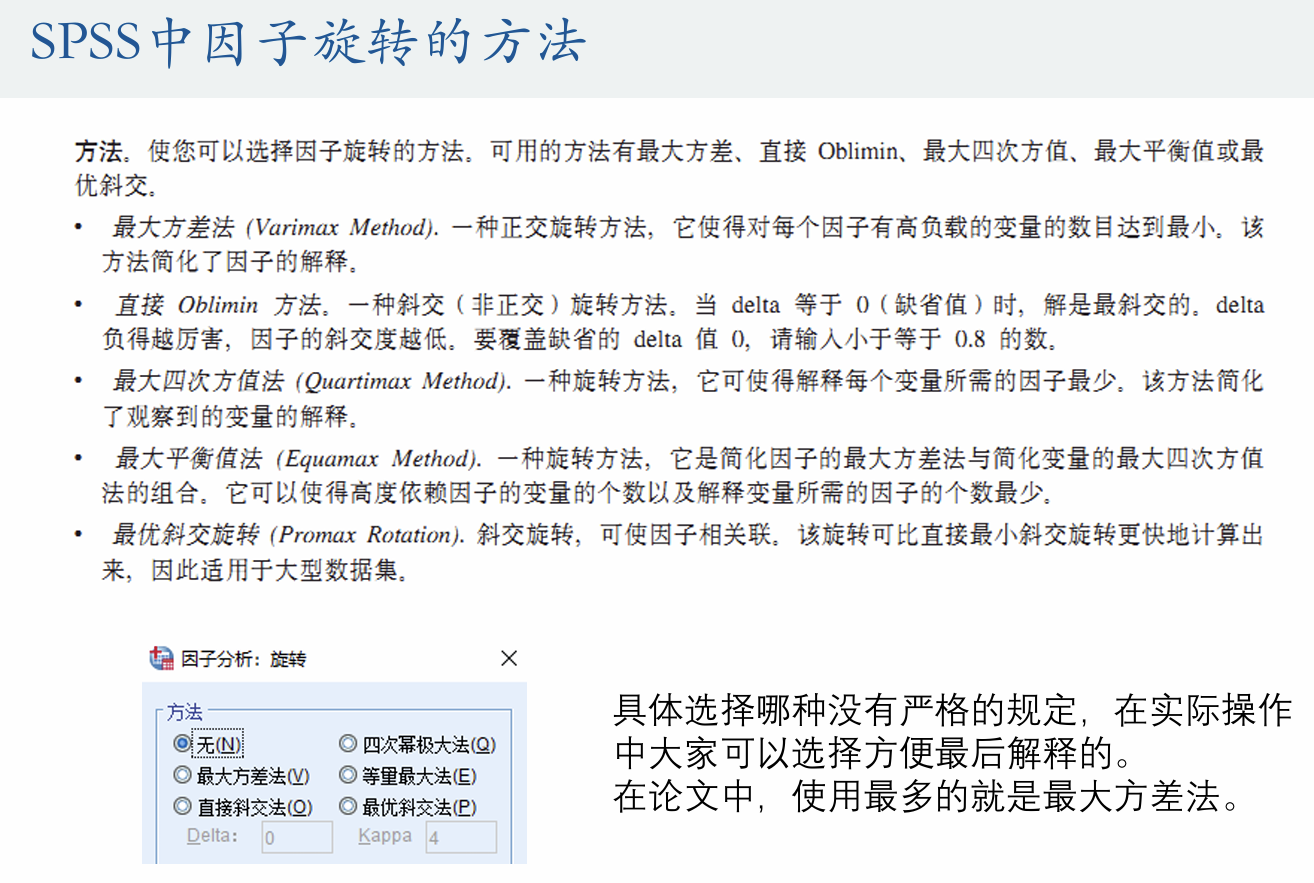
5.因子旋转的方法

我们虽然解出了A，但是这个A不一定符合我们的要求，因此我们需要对其进行正交旋转，这样方便我们进行解释。
在SPSS中已经给出了各个方法

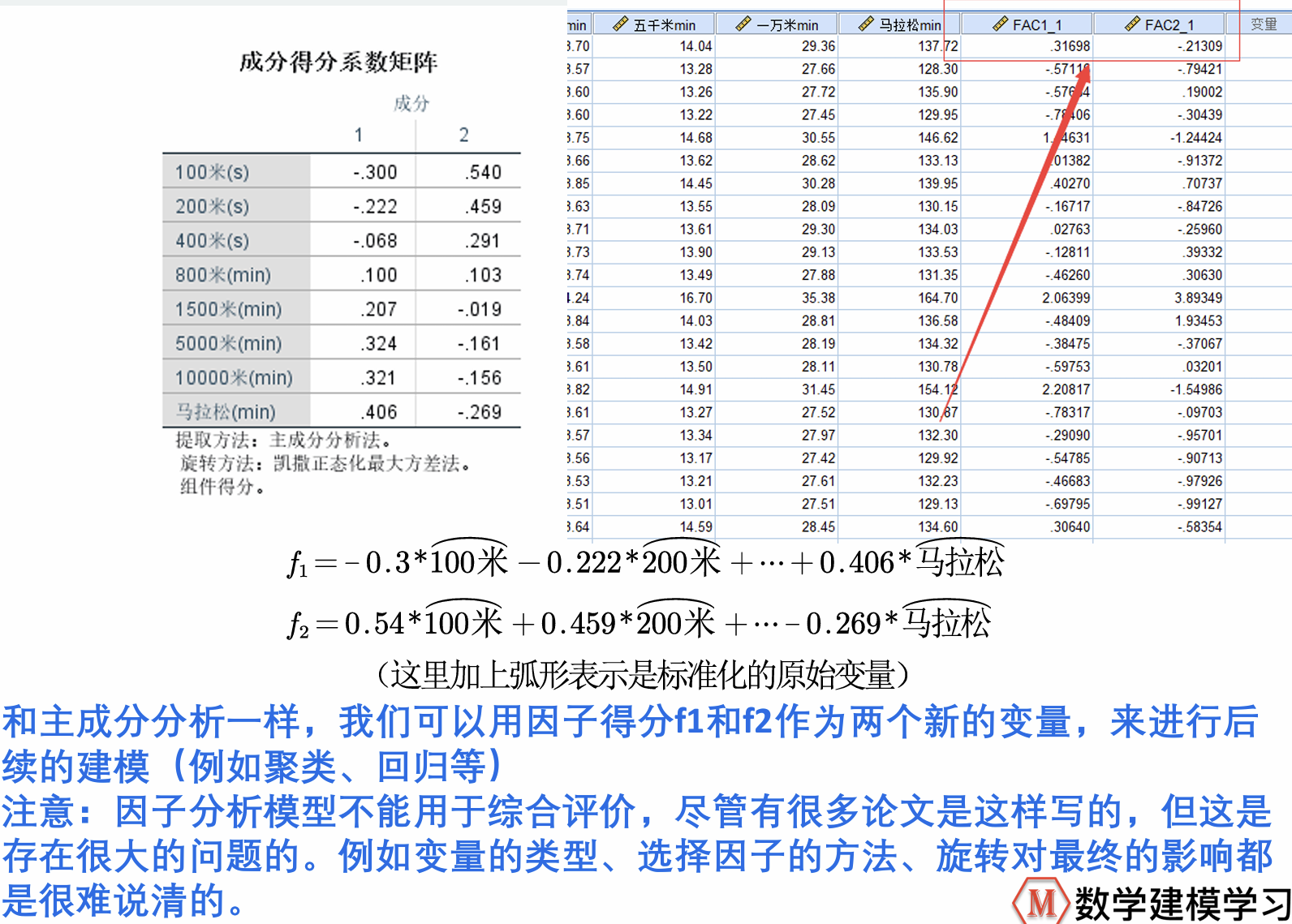
6.因子得分

因子分析是将变量表示为公共因子和特殊因子的线性组合；此外，我们可以反过来将公共因子表示为原变量的线性组合，即可得到因子得分
实现这一步骤的方法，SPSS给给出了

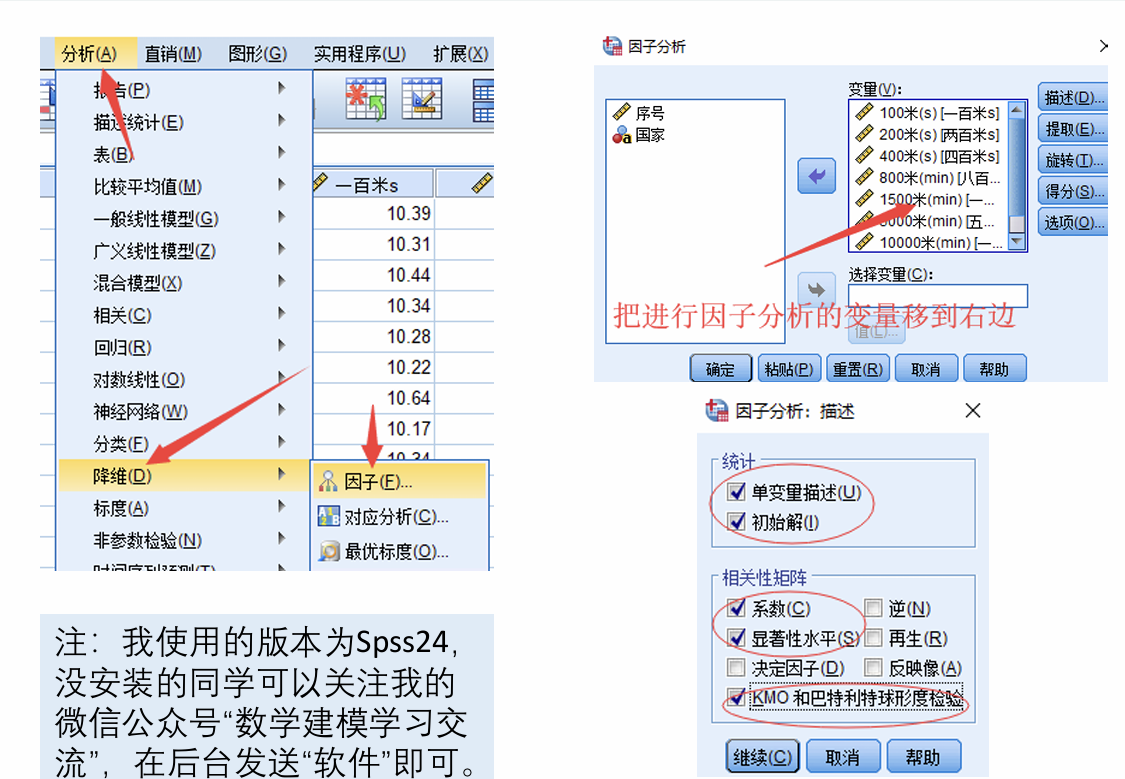
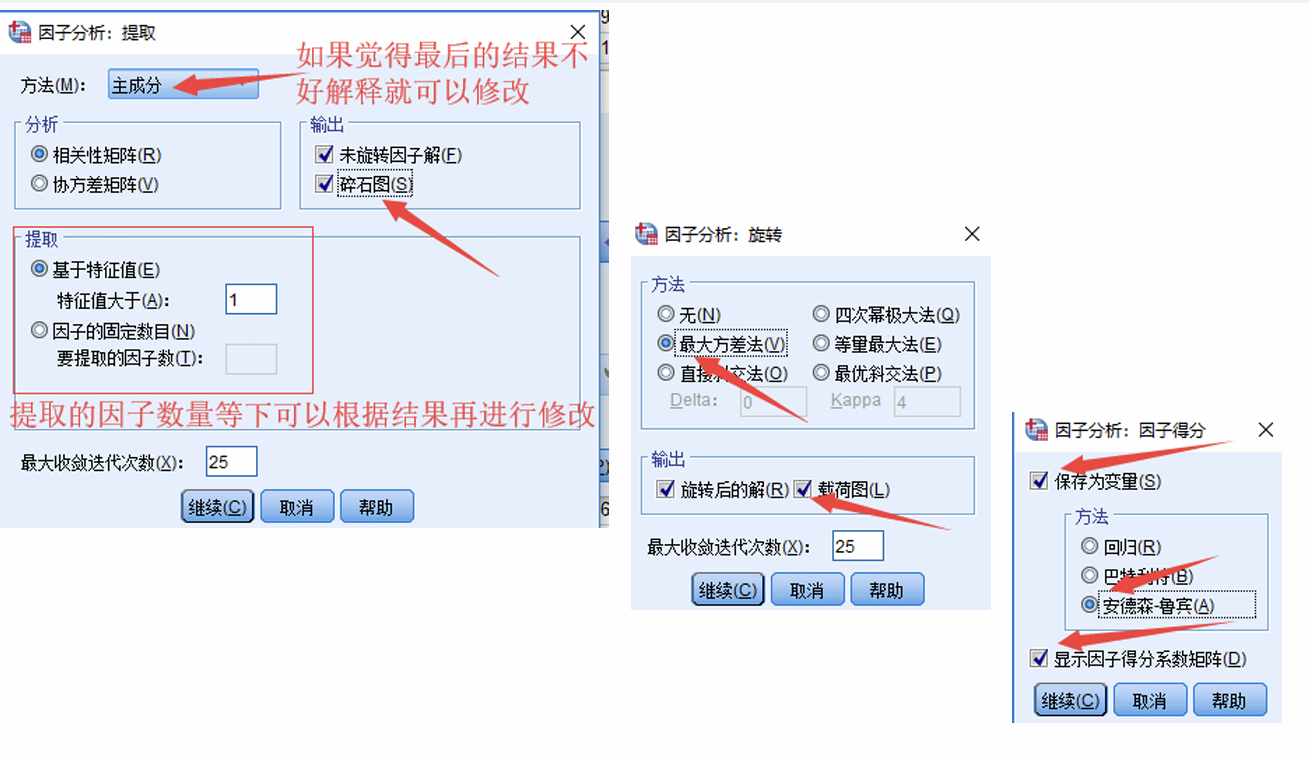
四、因子分析的操作步骤

操作步骤只需要按照下图设置好即可,选项的选择我们会在下方的结果分析一一介绍。
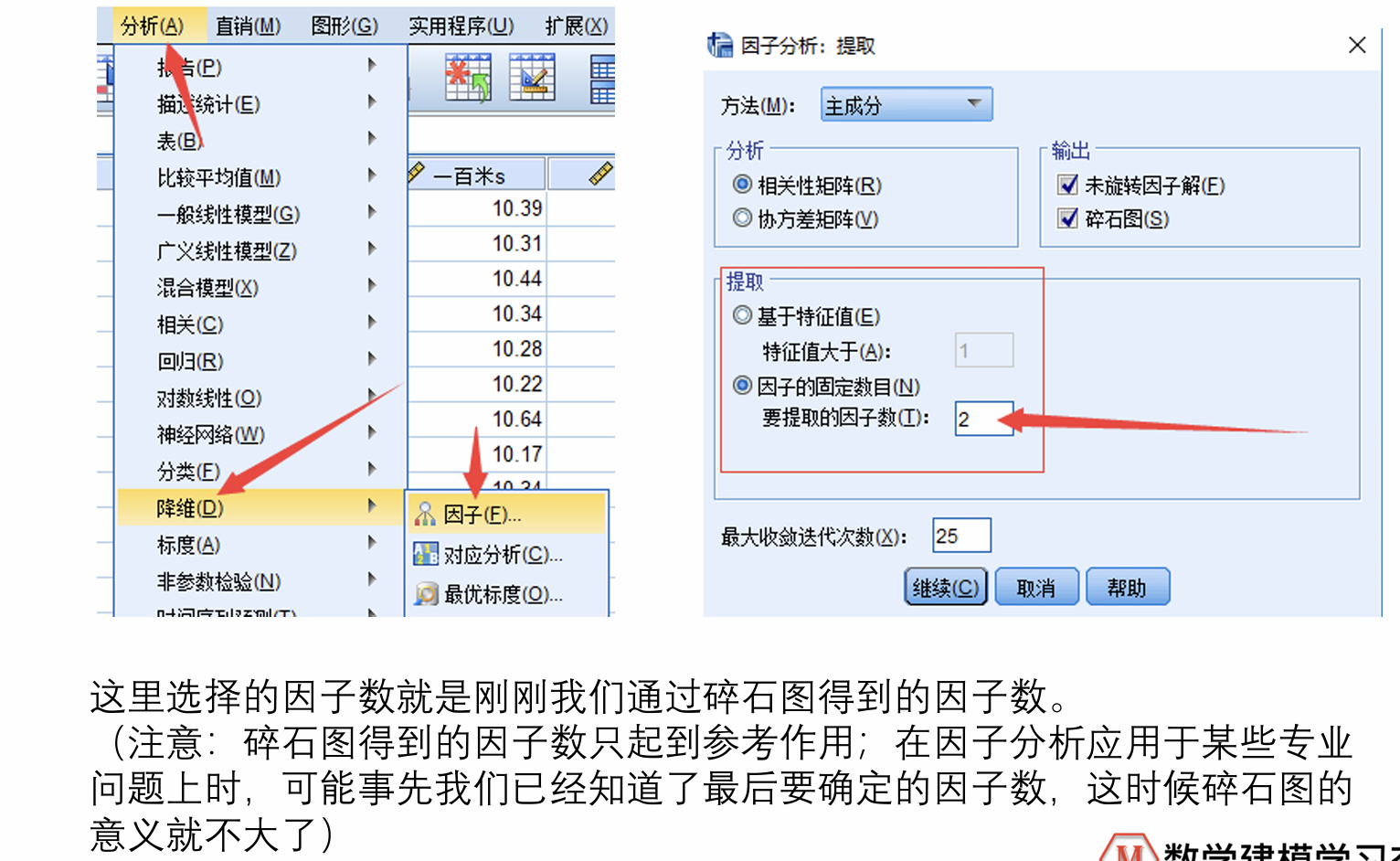
要注意，因子分析要进行两次，通过第一次得到的碎石图固定出得到因子的数目

五、结果分析

1.模型检验

（1）KMO检验和巴特利特球形检验。

KMO统计量是取值在0和1之间，意味着变量间的相关性越强，原有变量越适合作因子分析；当所有变量间的简单相关系数平方和接近0时，KMO值越接近于0,意味着变量间的相关性越弱，原有变量越不适合作因子分析。
KMO检验标准：KMO>0.9,非常适合；0.8<KMO<0.9,适合；0.7<KMO<0.8, 一般；0.6<KMO<0.7,不太适合；KMO<0.5,不适合

（2）巴特利特球形检验

巴特利特球形检验是一种检验各个变量之间相关性程度的检验方法。一般在做因子分析之前都要进行巴特利特球形检验，用于判断变量是否适合用于做因子分析。
它的原假设是相关系数矩阵是一个单位阵（不适合做因子分析，指标之间的相关性太差，不适合降维），因此拒绝原假设即认为适合做因子分析

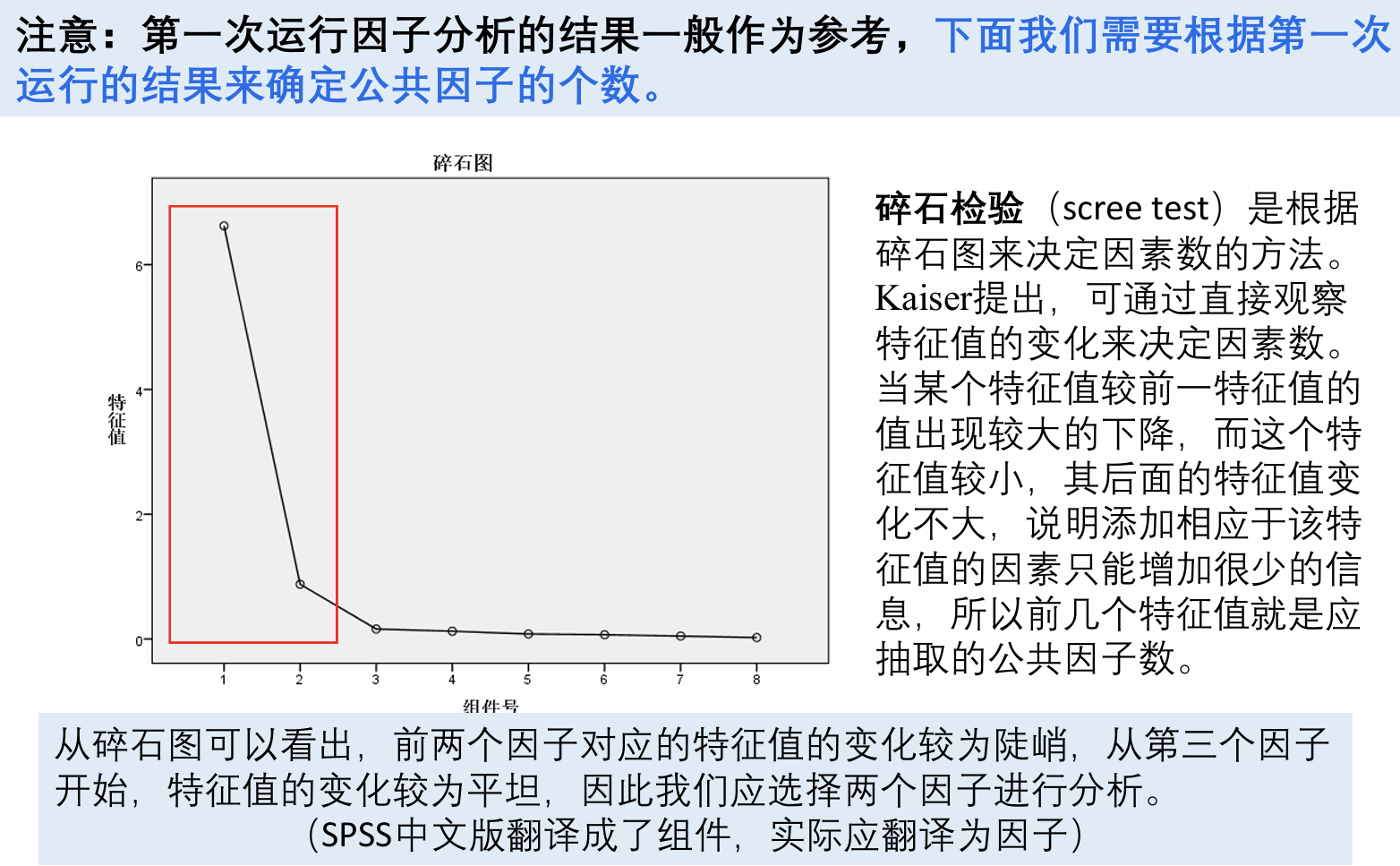
2.确定因子的数目

观察碎石图，选择较为陡峭的因子作为因子数

3.调整因子个数重新计算

4.公因子方差

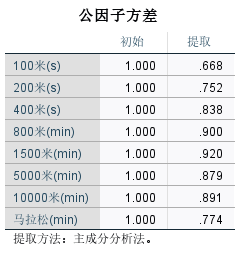
800米(s)这个变量的公因子方差为0.9，这可以解释为我们提取的两个公共因子对100米(s)这个变量的方差贡献率为90%，即这两个公共因子能够反映出（或者说保留）100米(s)这个变量90%的信息

5.总方差解释表

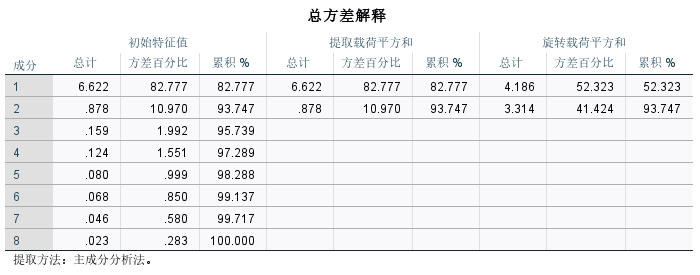
（1）初始特征值

从“初始特征值”一栏中可以看出，前2个公共因子解释的累计方差达93.747%，而后面的公共因子的特征值较小，对解释原有变量的贡献越来越小，因此提取两个公共因子是合适的

（2）载荷平方和

“提取载荷平方和” 一栏是在未旋转时被提取的2个公共因子的方差贡献信息，其与“初始特征值”栏的前两行取值一样。
“旋转载荷平方和”是旋转后得到的新公共因子的方差贡献信息，每个公共因子的方差贡献率有变化，这一步骤相当于把贡献率给平均化了，便于我们解释。但最终的累计方差贡献率不变。

6.成分矩阵

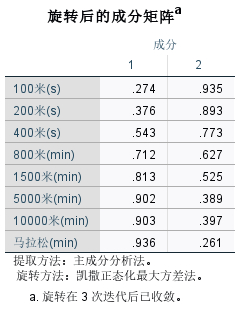
旋转后的每个公共因子上的载荷分配更清晰，因而比未旋转时更容易解释各因子的意义。我们在实际应用中只用关注旋转后的因子载荷矩阵即可。
因子载荷是变量与公共因子的相关系数，当某变量在某公共因子中的载荷绝对值越大，表明该变量与该公共因子更密切，即该公共因子更能代表该变量，其最大值为1。

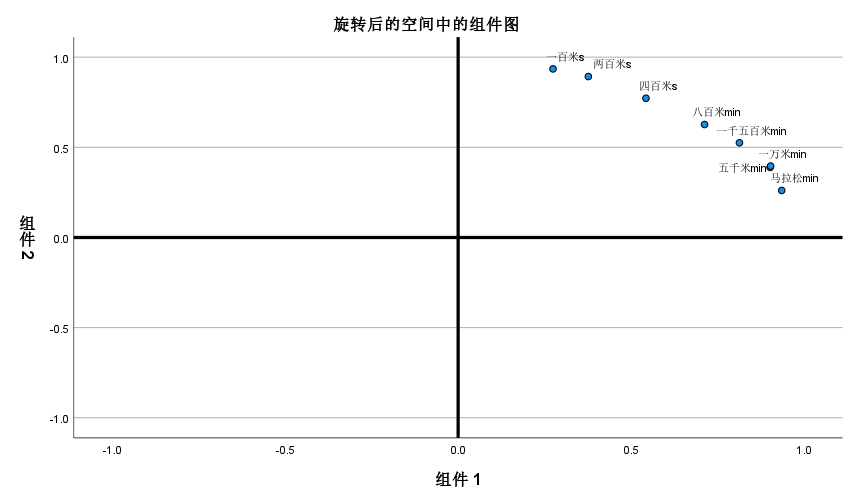
7.旋转后的因子载荷散点图

根据“旋转后的成分矩阵”的两列数据所作，由此图观察所得信息与从“旋转成分矩阵”所得信息一致。（如果有三个因子，那么画出来的图就是三维图）

8.因子得分