多项式全家桶

多项式合集

前置知识：多项式的定义，表示方法，FFT，NTT，微积分等。

注意事项

1. 多项式的封装很重要，现在一般都是用将指针传入一个函数的方式来进行多项式操作，如：void Inv(ll *f,ll *g,int n)，表示对 \(n\) 次多项式 \(f\) 求逆，结果存在 \(g\) 中。
2. 多项式数组多了一定要记得清空！！说的直接点，不要觉得你的空间很宝贵，现在一般 \(10^5\) 的数据范围能够你开 \(100\) 个数组！所以如果两个函数可能会共用一个数组的时候一定不要冒风险，该多开数组就开。

多项式乘法

模板

所有多项式操作的基础，这里提供一篇小学生也能看懂的博客，真的特别详细！从复数到单位根到优化全部讲了一遍，这里仅提供一下代码：

1. FFT

struct node
{double x,y;friend node operator +(node a,node b){return {a.x+b.x,a.y+b.y};}friend node operator -(node a,node b){return {a.x-b.x,a.y-b.y};}friend node operator *(node a,node b){return {a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
}f[N],g[N];
void FFT(node *f,int type)
{for(int i = 0;i < lim;i++)if(i < tr[i])swap(f[i],f[tr[i]]);for(int l = 2;l <= lim;l <<= 1){node wn = {cos(2*Pi/l),sin(2*Pi/l)*type};int now = l>>1;for(int s = 0;s < lim;s += l){node w = {1,0};int up = s|now;for(int i = s;i < up;i++,w = w*wn){node mul = w*f[i|now];f[i|now] = f[i]-mul;f[i] = f[i]+mul;}}}if(~type)return ;for(int i = 0;i < lim;i++)f[i].x = f[i].x/lim+0.5,f[i].y = f[i].y/lim+0.5;
}

int main()
{n = rd();m = rd();for(int i = 0;i <= n;i++)f[i].x = rd();for(int i = 0;i <= m;i++)g[i].x = rd();while(lim <= n+m)lim <<= 1;for(int i = 0;i < lim;i++)tr[i] = tr[i>>1]>>1|((i&1)?lim>>1:0);FFT(f,1);FFT(g,1);for(int i = 0;i < lim;i++)f[i] = f[i]*g[i];FFT(f,-1);for(int i = 0;i <= n+m;i++)printf("%d ",(int)f[i].x);return 0;
}

2. NTT

\(FFT\) 的计算要用到小数，而小数不可避免会有精度问题，而且大多数情况下运算都是在模意义下进行的，所以就有了 \(NTT\)。

\(NTT\) 事实上就是将 \(FFT\) 的单位根换成了原根，其他其实是完全一样的。

一般来说 \(NTT\) 的模数都是 \(998244353\)，因为 \(998244353=119\times 2^{23}+1\)，而一般情况下 \(n\) 肯定不会达到 \(2^{23}\)。如果模数不为 \(998244353\)，那么可以考虑用三个模数分别做再 \(CRT\) 合并，详见P4245【模板】任意模数多项式乘法。

这里也只是给出 \(NTT\) 模板的代码：

ll qp(ll x,int y)
{ll ans = 1;for(;y;y >>= 1,x = x*x%mod)if(y&1)(ans *= x) %= mod;return ans;
}
int G = 3,invG = qp(3,mod-2),inv2 = qp(2,mod-2);
int jia(int x,int y){return x+y >= mod?x+y-mod:x+y;}
int jian(int x,int y){return x < y?x-y+mod:x-y;}
void NTT(ll *f,int type)
{for(int i = 0;i < lim;i++)if(i < tr[i])swap(f[i],f[tr[i]]);for(int l = 2;l <= lim;l <<= 1){ll wn = qp(~type?G:invG,(mod-1)/l);int now = l>>1;for(int s = 0;s < lim;s += l){ll w = 1;for(int i = s;i < s+now;i++,w = w*wn%mod){int mul = w*f[i+now]%mod;f[i+now] = jian(f[i],mul);f[i] = jia(f[i],mul);}}}
}

int main()
{n = rd();m = rd();for(int i = 0;i <= n;i++)f[i] = rd();for(int i = 0;i <= m;i++)g[i] = rd();while(lim <= n+m)lim <<= 1;for(int i = 0;i < lim;i++)tr[i] = tr[i>>1]>>1|((i&1)?lim>>1:0);NTT(f,1);NTT(g,1);for(int i = 0;i <= lim;i++)f[i] = f[i]*g[i]%mod;NTT(f,-1);int invn = qp(lim,mod-2);for(int i = 0;i <= n+m;i++)printf("%lld ",f[i]*invn%mod);return 0;
}

---

在正式进入多项式全家桶前，还要介绍一些用于简化操作的函数：

1. void cpy(ll *al,ll *ar,ll *b)：表示将al到ar的数复制到b中。

void cpy(ll *al,ll *ar,ll *b){for(int i = 0;al != ar;al++,i++)*(b+i) = *al;}

1. void clr(ll *al,ll *ar)：表示将al到ar的数全部赋值为 \(0\)。

void clr(ll *al,ll *ar){for(;al != ar;al++)*al = 0;}

1. void pri(ll *f,int n)，表示输出 \(n\) 次多项式 \(f\)。

void pri(ll *f,int n)
{for(int i = 0;i <= n;i++)printf("%lld%c",f[i],i==n?'\n':' ');
}

并且，我们还要对多项试卷积进行封装：

void init(n)：表示初始化 \(n\) 次多项式的蝴蝶变换数组。

void init(int n)
{lim = 1;while(lim <= n)lim <<= 1;for(int i = 0;i < lim;i++)tr[i] = tr[i>>1]>>1|(i&1?lim>>1:0);
}

void times(ll *f,ll *g,ll *a,int n,int m)：表示求 \(f\) 和 \(g\) 的卷积，结果存在 \(a\) 中。

void times(ll *f,ll *g,ll *a,int n,int m)
{cpy(f,f+n+1,a);cpy(g,g+m+1,b);init(n+m);clr(a+n+1,a+lim);clr(b+m+1,b+lim);NTT(a,1);NTT(b,1);for(int i = 0;i <= lim;i++)a[i] = a[i]*b[i]%mod;NTT(a,-1);
}

这里先将 \(f\) 和 \(g\) 复制到了另一个数组中再进行的卷积，并且会卷积前会将不用的东西清空——以后实现的每个函数都应该这样：传进去的参数不应该会发生改变，也不用提前清空不必要的东西。

讲了这么多，终于要开始多项式全家桶了（

---

多项式求逆

P4238【模板】多项式乘法逆

给定一个 \(n-1\) 次多项式 \(F(x)\)，求多项式 \(G(x)\) 使得 \(F(x) \times G(x)\equiv 1\pmod{x^n}\)。

---

如果只有一项，显然这一项就是 \(F_0\) 的逆元，于是可以递归分治求解。

现在假设已经求出了 \(F(x)G_0(x)\equiv 1\pmod{x^{\lceil\frac n 2\rceil}}\)

又因为 \(F(x)G(x)\equiv 1\pmod{x^{\lceil\frac n 2\rceil}}\)，所以两式相减得：\(F(x)(G(x)-G_0(x))\equiv 0\pmod{x^{\lceil\frac n 2\rceil}}\)。

所以 \(G(x)-G_0(x)\equiv 0\pmod{x^{\lceil\frac n 2\rceil}}\)。

两边同时平方，由于 \(G(x)-G_0(x)\) 在模 \(x^{\lceil\frac n 2\rceil}\) 意义下等于 \(0\)，所以 \((G(x)-G_0(x))^2\) 在模 \(x^n\) 意义下就是 \(0\)。

所以 \(G^2(x)+G_0^2(x)-2G(x)G_0(x) \equiv 0 \pmod{x^n}\)

两边同时乘 \(F(x)\)，因为 \(F(x)G(x) \equiv 1 \pmod {x^n}\)，所以 \(G(x)+F(x)G_0^2(x)-2G_0(x) \equiv 0 \pmod{x^n}\)

所以 \(G(x) \equiv G_0(x)(2-F(x)G_0(x)) \pmod{x^n}\)，然后就可以递归做了。

void Inv(ll *f,ll *g,int n)//G = G0(2-FG0)
{if(!n)return (void)(g[0] = qp(f[0],mod-2));Inv(f,g,n>>1);init(n << 1);cpy(f,f+n+1,a);clr(a+n+1,a+lim);clr(g+n+1,g+lim);NTT(a,1);NTT(g,1);for(int i = 0;i < lim;i++)g[i] = g[i]*(2-a[i]*g[i]%mod+mod)%mod;NTT(g,-1);clr(g+n+1,g+lim);
}

分治 \(FFT\)

P4721 【模板】分治 FFT

给定序列 \(g_{1\dots n - 1}\)，求序列 \(f_{0\dots n - 1}\)。

其中 \(f_i=\sum_{j=1}^if_{i-j}g_j\)，边界为 \(f_0=1\)。

---

这题也可以用多项式求逆来做：\(F(x) = \frac{1}{1-G(x)}\)，具体证明看题解吧

下面是分治的做法：

假设我们已经求出了 \(G_{[l,mid]}\) 这一区间的数，现在我们要求 \(G_{[l,mid]}\) 对 \(G_{[mid+1,r]}\) 的贡献。

根据定义可以发现：\(G_{[l,mid]}\) 对 \(G_{[mid+1,r]}\) 的贡献事实上就是 \(G_{[l,mid]} \times F_{[0,r-l]}\)，只需要做一遍卷积，然后再加到对应位置上即可。

为什么是 \(F_{[0,r-l]}\) 而不是 \(F_{[0,r-mid]}\)？因为你要考虑所有 \(G_{[l,mid]}\) 对 \(G_{[mid+1,r]}\) 的贡献。就比如 \(G_l\) 乘 \(F_{r-l}\) 就对 \(G_r\) 有贡献，所以最大应该取到 \(F_{r-l}\) 而不是 \(F_{r-mid}\)。

void CDQ(ll *f,ll *g,int l,int r)//Inverse:F = 1/(1-G)(mod x^n)
{if(l == r)return ;int mid = l+r>>1;CDQ(f,g,l,mid);times(f,g+l,a,r-l,mid-l);for(int i = mid+1;i <= r;i++)g[i] = jia(g[i],a[i-l]);CDQ(f,g,mid+1,r);
}

多项式除法

P4512 【模板】多项式除法

给定一个 \(n\) 次多项式 \(F(x)\) 和一个 \(m\) 次多项式 \(G(x)\) ，求多项式 \(Q(x)\) 和 \(R(x)\)，满足以下条件：

• \(Q(x)\) 次数为 \(n-m\)，\(R(x)\) 次数小于 \(m\)
• \(F(x) = Q(x) * G(x) + R(x)\)

---

设 \(F\) 是一个 \(n\) 次多项式，另 \(F_r(x)\) 表示将 \(F(x)\) 的 \(0-n\) 次项的系数翻转一遍后的多项式，可以发现其实 \(F_r(x) = x^nF(\frac 1 x)\)。

\[F(x) = Q(x) \times G(x)+R(x) \\ F(\frac 1 x) = Q(\frac 1 x) \times G(\frac 1 x)+R(\frac 1 x) \\ x^n F(\frac 1 x) = x^{n-m} Q(\frac 1 x) \times x^m G(\frac 1 x)+x^{n-m+1} \times x^{m-1} R(\frac 1 x) \\ F_r(x) = Q_r(x) \times G_r(x)+x^{n-m-1} \times R_r(x) \\ \]

因为 \(Q_r\) 是 \(n-m\) 次的，所以如果要求出 \(Q\)，我们完全可以在模 \(x^{n-m+1}\) 意义下进行求解，而刚好 \(R_r(x)\) 乘了个 \(x^{n-m+1}\)，所以可以直接丢掉。

那么 \(F_r(x) \equiv Q_r(x) \times G_r(x) \pmod{x^{n-m+1}}\)，所以 \(Q_r(x) \equiv \frac{F_r(x)}{G_r(x)} \pmod{x^{n-m+1}}\)。

于是可以算出 \(Q(x)\)，然后 \(R(x) = F(x)-Q(x) \times G(x)\)，就可以求出 \(R(x)\) 了。

void rvs(ll *f,ll *g,int n)//求F_r，存到G里面，F和G有可能是一个东西
{for(int i = 0;i <= n/2;i++){ll t = f[i];g[i] = f[n-i];g[n-i] = t;}}
ll inv_rvsg[N];
void div(ll *f,ll *g,ll *q,ll *r,int n,int m)//F = Q*G+R,Qr = Fr/Gr
{rvs(f,q,n);rvs(g,g,m);Inv(g,inv_rvsg,n-m);times(q,inv_rvsg,q,n,n-m);clr(q+n-m+1,q+lim);rvs(q,q,n-m);rvs(g,g,m);times(g,q,a,m,n-m);for(int i = 0;i <= m-1;i++)r[i] = jian(f[i],a[i]);
}

多项式开根

P5205 【模板】多项式开根

给定一个 \(n-1\) 次多项式 \(F(x)\)，求多项式 \(G(x)\) 使得 \(G^2(x)\equiv F(x)\pmod{x^n}\)。保证 \(F_0 = 1\)。

---

多项式开根和求逆其实差不多。

如果只有一项，显然这一项就是 \(1\)，也是考虑递归分治求解。

现在假设已经求出了 \(G_0^2(x)\equiv F(x)\pmod{x^{\lceil\frac n 2\rceil}}\)，因为 \(G^2(x)\equiv F(x)\pmod{x^{\lceil\frac n 2\rceil}}\)，所以：

\[G(x)-G_0(x)\equiv 0\pmod{x^{\lceil\frac n 2\rceil}} \\ (G(x)-G_0(x))^2 \equiv 0\pmod{x^n} \\ G^2(x)+G_0^2(x)-2G(x)G_0(x) \equiv 0\pmod{x^n} \\ F(x)+G_0^2(x)-2G(x)G_0(x) \equiv 0\pmod{x^n} \\ G(x) \equiv \frac{F(x)+G_0^2(x)}{2G_0(x)} \pmod{x^n} \]

为了写代码方便，这里再继续化成：\(G(x) \equiv \frac 1 2(\frac{F(x)}{G_0(x)}+G_0(x))\)。然后就可以做了。

ll invg[N];
void Sqrt(ll *f,ll *g,int n)//G = (F+G0^2)/2G0
{if(!n)return (void)(g[0] = 1);Sqrt(f,g,n>>1);Inv(g,invg,n);times(invg,f,invg,n,n);for(int i = 0;i <= n;i++)g[i] = (invg[i]+g[i])*inv2%mod;clr(g+n+1,g+lim);
}

加强版

P5277 【模板】多项式开根（加强版）

与模板唯一不同的是，\(F_0\) 不一定是 \(1\)。

那么我们只需要修改一下边界条件，相当于求一次 \(F_0\) 的二次剩余。

由于 \(998244353\) 的原根是 \(3\)，那么 \(F_0\) 一定可以表示为 \(3^t\)，用 \(BSGS\) 求出即可。又因为题目保证了 \(F_0\) 有二次剩余，所以 \(F_0\) 的二次剩余就是 \(3^{\frac t 2}\)。

int BSGS(int a,int b)
{mp.clear();ll m = sqrt(mod)+1,now = b;for(int i = 0;i <= m;i++,now = now*a%mod)mp[now] = i;ll sum = qp(a,m);now = sum;for(int i = 1;i <= m;i++,now = now*sum%mod)if(mp.count(now))return i*m-mp[now];return -1;
}
int residue(int x,int k)//求x的k次剩余
{int ans = qp(G,BSGS(G,x)/k);return min(ans,mod-ans);
}
void Sqrt(ll *f,ll *g,int n)//G = (F+G0^2)/2G0
{if(!n)return (void)(g[0] = residue(f[0],2));...
}

微积分

下面的部分就要涉及到微积分了，如果不知道的可以看这：什么是微积分？

一些求导法则：

1. \((x^a)' = ax^{a-1}\)，\(\int x^adx = \frac{x^{a+1}}{a+1}\)
2. \((\ln x)' = \frac 1 x\)，\((e^x)' = e^x\)
3. \((f(x) \pm g(x))' = f'(x) \pm g'(x)\)
4. \((f(x)\times g(x))' = f'(x)g(x)+f(x)g'(x)\)
5. \((f(g(x)))' = f'(g(x))\times g'(x)\)
6. \((\frac{f(x)}{g(x)})' = \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\)

根据第一个求导法则，我们可以写出多项式的求导和积分函数：

void dao(ll *f,ll *g,int n)
{for(int i = 1;i <= n;i++)g[i-1] = f[i]*i%mod;g[n] = 0;}
void jifen(ll *f,ll *g,int n)
{for(int i = n;~i;i--)g[i+1] = f[i]*qp(i+1,mod-2)%mod;g[0] = 0;}

多项式对数函数

P4725 【模板】多项式对数函数（多项式 ln）

给定一个 \(n-1\) 次多项式 \(F(x)\)，求多项式 \(G(x)\) 使得 \(G(x)\equiv \ln F(x) \pmod{x^n}\)。保证 \(F_0 = 1\)。

---

对 \(G(x)\equiv \ln F(x) \pmod{x^n}\) 两边同时求导得：\(G'(x) \equiv \frac{F'(x)}{F(x)} \pmod{x^n}\)

所以 \(G(x) \equiv \int\frac{F'(x)}{F(x)}dx \pmod{x^n}\)

ll invf[N];
void ln(ll *f,ll *g,int n)//G=jifen(F'[i]/F[i])
{Inv(f,invf,n);dao(f,g,n);times(g,invf,g,n,n);clr(g+n+1,g+lim);jifen(g,g,n-1);
}

牛顿迭代

给定一个 \(n-1\) 次多项式 \(F(x)\)，已知有多项式 \(G(x)\) 满足 \(F(G(x)) \equiv 0 \pmod {x^n}\)，求 \(G(x)\)。

先来看一个简单的问题：如何对一个很大的数 \(a\) 开方？很显然可以二分，但是二分每次都要算一个很大的数的平方，有没有什么更快的方法？

于是牛顿迭代产生了。

我们本质上是要求 \(f(x) = x^2-a\) 与 \(0\) 的交点。假设我们已经求得了一个近似值 \(x_0\)，牛顿迭代的做法即为过 \((x_0,f(x_0))\) 这个点做函数的切线，取切线与 \(x\) 轴的交点作为新的 \(x_0\)。

比如我们要求 \(\sqrt{50}\)（图是盗的）：

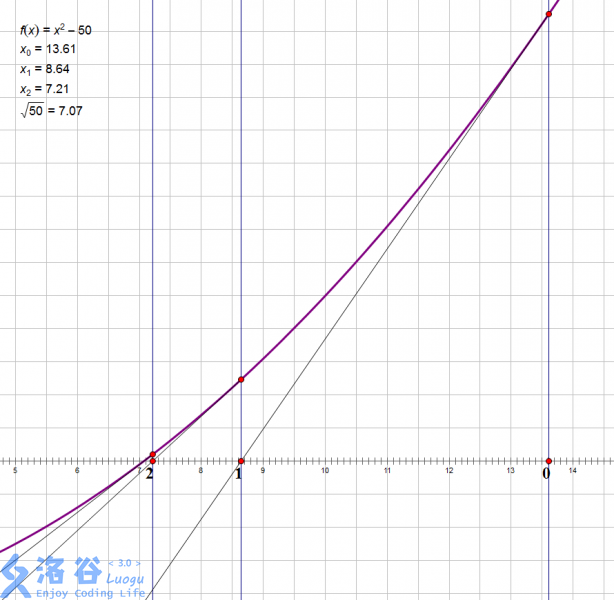
具体的，我们要求一条过 \((x_0,f(x_0))\)，斜率为 \(f'(x_0)\) 的直线与 \(x\) 轴的交点。

很容易得出，切线方程为 \(y = f'(x_0)(x-x_0)+f(x_0)\)，当 \(y = 0\) 时，\(x = x_0-\frac{f(x_0)}{f'(x_0)}\)

再回到原来的问题：求函数 \(G(x)\)，使得 \(F(G(x)) \equiv 0 \pmod {x^n}\)。

假设我们已经求出了 \(F(G_0(x)) \equiv 0\)，那么只需要每次令：

\[G(x)\equiv G_0(x)-\frac{F(G_0(x))}{F'(G_0(x))} \]

事实上，牛顿迭代每次都会让精度翻倍，即如果 \(F(G_0(x))\equiv 0\pmod{x^{\lceil\frac n 2\rceil}}\)，那么有 \(F(G(x) \equiv 0\pmod{x^n}\)。可以根据多项式求逆和开根感性理解。

多项式指数函数

P4726 【模板】多项式指数函数（多项式 exp）

给定一个 \(n-1\) 次多项式 \(F(x)\)，求多项式 \(G(x)\) 使得 \(G(x)\equiv e^{F(x)}\pmod{x^n}\)。保证 \(F_0 = 0\)。

---

因为 \(G(x)\equiv e^{F(x)}\pmod{x^n}\)，所以 \(\ln G(x) - F(x) \equiv 0\)。

根据牛顿迭代，我们可以令函数 \(f(G(x)) = \ln G(x)-F(x) \equiv 0\)，有 \(f'(G_0(x)) = \frac 1 {G_0(x)}\)（注意一下这里不是复合函数求导）。

由牛顿迭代得：

\[\begin{align} G(x) &\equiv G_0(x)-\frac{f(G_0(x))}{f'(G_0(x))} \\ &= G_0(x)-\frac{\ln G_0(x)-F(x)}{\frac 1 {G_0(x)}} \\ &= G_0(x)(1-\ln G_0(x)+F(x)) \end{align} \]

然后就可以递归去做了。

ll lng[N];
void exp(ll *f,ll *g,int n)//G = G0(1-lnG0+F)
{if(!n)return (void)(g[0] = 1);exp(f,g,n>>1);ln(g,lng,n);for(int i = 0;i <= n;i++)lng[i] = jian(!i+f[i],lng[i]);times(g,lng,g,n,n);clr(g+n+1,g+lim);
}

再看多现实求逆和开方

在看到多项式求逆和开方的做法时，你可能会有点懵，为啥使用递归分治来做？为啥求了当前一半的答案就可以算出当前整个的答案？下面，我们再从牛顿迭代的角度推一遍。

多项式求逆

给定一个 \(n-1\) 次多项式 \(F(x)\)，求多项式 \(G(x)\) 使得 \(F(x) \times G(x)\equiv 1\pmod{x^n}\)。

令函数 \(f(G(x)) = \frac 1 {G(x)}-F(x) \equiv 0\)，有 \(f'(G(x)) = -\frac 1 {G^2(x)}\)。

由牛顿迭代得：

\[\begin{align} G(x) &\equiv G_0(x)-\frac{f(G_0(x))}{f'(G_0(x))} \\ &= G_0(x)-\frac{\frac 1 {G_0(x)}-F(x)}{-\frac 1 {G_0^2(x)}} \\ &= G_0(x)(2-F(x)G_0(x)) \end{align} \]

是不是和之前推出来的式子完全一样？现在知道为啥要递归去做了吧！

多项式开方

给定一个 \(n-1\) 次多项式 \(F(x)\)，求多项式 \(G(x)\) 使得 \(G^2(x) \equiv F(x)\pmod{x^n}\)。

令函数 \(f(G(x)) = G^2(x)-F(x) \equiv 0\)，有 \(f'(G(x)) = 2G(x)\)。

由牛顿迭代得：

\[\begin{align} G(x) &\equiv G_0(x)-\frac{f(G_0(x))}{f'(G_0(x))} \\ &= G_0(x)-\frac{G_0^2(x)-F(x)}{2G_0(x)} \\ &= \frac{G_0^2(x)+F(x)}{2G_0(x)} \end{align} \]

多项式快速幂

P5245 【模板】多项式快速幂

给定一个 \(n-1\) 次多项式 \(F(x)\) 和 \(k\)，求多项式 \(G(x)\) 使得 \(G(x) \equiv F^k(x)\pmod{x^n}\)。保证 \(F_0 = 1\)。

---

显然可以像普通快速幂一样直接做，但是这样子是 \(\mathcal{O}(n\log^2n)\) 的，有没有更快的方法？

考虑对 \(G(x) \equiv F^k(x)\) 两边同时取对数得 \(\ln G(x) \equiv k\ln F(x)\)，

然后再取指数得：\(G(x) \equiv e^{k\ln F(x)}\)，这样子就可以 \(\mathcal{O}(n\log n)\) 做了。

void qpow(ll *f,ll *g,int n,int k)//G = e^{k*lnF}
{ln(f,lnf,n);for(int i = 0;i <= n;i++)lnf[i] = lnf[i]*k%mod;exp(lnf,g,n);
}

加强版

P5273 【模板】多项式幂函数（加强版）

给定一个 \(n-1\) 次多项式 \(F(x)\) 和 \(k\)，求多项式 \(G(x)\) 使得 \(G(x) \equiv F^k(x)\pmod{x^n}\)。不保证 \(F_0 = 1\)。

---

如果 \(F_0 \ne 1\)，那么可以考虑先给多项式除以一个 \(F_0\)，然后做快速幂，最后再乘上 \(F_0^k\)。

但是还有一种可能——\(F_0 = 0\)，这种情况下需要找到最低的系数不为 \(0\) 的那一项。

设这一项为 \(c\times x^d\)，那么让整个多项式除以这一项就能保证第一项为 \(1\) 了。做了快速幂之后再让整个多项式乘 \(c^k\times x^{dk}\) 即可。

要注意的是 \(c^k\) 应该对 \(\varphi(998244353)\) 取模，而不是对 \(998244353\)。还要注意判断 \(dk\) 是否比 \(n\) 大，所以在读入模数时应该记录三个值。

ll ff[N];
void exqpow(ll *f,ll *g,int n,char *s)//f = ff*(c*x^d)
{int len = strlen(s+1);ll k1 = 0,k2 = 0,k3 = 0;for(int i = 1;i <= len;i++){k1 = (k1*10+(s[i]^48))%mod;k2 = (k2*10+(s[i]^48))%phimod;if(i <= 6)k3 = k3*10+(s[i]^48);}ll c = 0,d,invc;for(int i = 0;i <= n;i++){if(!c&&f[i])invc = qp(c = f[i],mod-2),d = i;if(c)ff[i-d] = f[i]*invc%mod;}if(!c)return (void)clr(g,g+n+1);qpow(ff,g,n,k1);d = min(n+1ll,d*k3);c = qp(c,k2);for(int i = n;~i;i--)g[i] = i < d?0:g[i-d]*c%mod;
}

多项式三角函数

P5264 多项式三角函数

给定一个 \(n-1\) 次多项式 \(F(x)\)，求多项式 \(G(x)\) 使得 \(G(x) \equiv \sin F(x)\pmod{x^n}\) 或 \(G(x) \equiv \cos F(x)\pmod{x^n}\)。保证 \(F_0 = 0\)。

---

首先你需要知道大名鼎鼎的欧拉公式：\(e^{i\theta} = \cos\theta + i\sin\theta\)

取 \(\theta = x\)：\(e^{ix} = \cos x + i\sin x\)；取 \(\theta = -x\)：\(e^{-ix} = \cos x - i\sin x\)

两式相加再除以 \(2\) 得 \(\cos x = \frac{e^{ix}+e^{-ix}}{2}\)；两式相加再除以 \(2i\) 得 \(\sin x = \frac{e^{ix}-e^{-ix}}{2i}\)；

还有个问题，\(i\) 在模意义下是多少？

因为 \(i^2 = -1\)，所以 \(i^2 \equiv 998244352 \pmod{998244353}\)，求一遍二次剩余即可。

ll I = residue(mod-1,2),invI = mod-I;

ll expg[N],inv_expg[N];
void sin(ll *f,ll *g,int n)//sinx = (e^ix-e^-ix)/2i
{for(int i = 0;i <= n;i++)g[i] = f[i]*I%mod;exp(g,expg,n);Inv(expg,inv_expg,n);int mul = inv2*invI%mod;for(int i = 0;i <= n;i++)g[i] = (expg[i]-inv_expg[i]+mod)*mul%mod;
}
void cos(ll *f,ll *g,int n)//cosx = (e^ix+e^-ix)/2
{for(int i = 0;i <= n;i++)g[i] = f[i]*I%mod;exp(g,expg,n);Inv(expg,inv_expg,n);for(int i = 0;i <= n;i++)g[i] = (expg[i]+inv_expg[i])*inv2%mod;
}

多项式反三角函数

P5265 多项式反三角函数

给定一个 \(n-1\) 次多项式 \(F(x)\)，求多项式 \(G(x)\) 使得 \(G(x) \equiv \arcsin F(x)\pmod{x^n}\) 或 \(G(x) \equiv \arctan F(x)\pmod{x^n}\)。保证 \(F_0 = 0\)。

有两个式子：

\[\arcsin x = \frac{\ln(ix+\sqrt{1-x^2})} i \\ \arctan x = \frac{\ln(1+ix)-\ln(1-ix)}{2i} \]

证：

1. \(\arcsin\)：

\[\arcsin x = \theta \Rightarrow x = \sin \theta = \frac{e^{i\theta}-e^{-i\theta}}{2i} \\ \]

令 \(p = e^{i\theta}\)：

\[x = \frac{p-\frac 1 p}{2i} \\ p^2-2ixp-1 = 0 \\ p = ix+\sqrt{1-x^2} \\ i\theta = \ln(ix+\sqrt{1-x^2}) \\ \theta = \frac{\ln(ix+\sqrt{1-x^2})} i \]

1. \(\arctan\)

\[\begin{align} \arctan x = \theta \Rightarrow x &= \frac{\sin \theta}{\cos\theta} \\ &= \frac{e^{i\theta}-e^{-i\theta}}{2i} \times \frac{2}{e^{i\theta}+e^{-i\theta}} \\ &= \frac{e^{i\theta}-e^{-i\theta}}{i(e^{i\theta}+e^{-i\theta})} \end{align} \]

令 \(p = e^{i\theta}\)：

\[x = \frac{p-\frac 1 p}{i(p+\frac 1 p)} \Rightarrow ix = \frac{p^2-1}{p^2+1} \\ (1-ix)p^2 = 1+ix \\ p = \sqrt{\frac{1+ix}{1-ix}} \\ \begin{align} i\theta &= \ln\sqrt{\frac{1+ix}{1-ix}} \\ &= \frac{\ln(1+ix)-\ln(1-ix)}{2} \end{align} \\ \theta = \frac{\ln(1+ix)-\ln(1-ix)}{2i} \]

证毕，套板子。

ll sqg[N];
void asin(ll *f,ll *g,int n)//asinx = ln(ix+sqrt(1-x^2))/i
{times(f,f,g,n,n);for(int i = 0;i <= n;i++)g[i] = jian(!i,g[i]);Sqrt(g,sqg,n);for(int i = 0;i <= n;i++)(sqg[i] += f[i]*I) %= mod;ln(sqg,g,n);for(int i = 0;i <= n;i++)(g[i] *= invI) %= mod;
}
ll lng1[N],lng2[N];
void atan(ll *f,ll *g,int n)//atanx = (ln(1+ix)-ln(1-ix))/2i
{for(int i = 0;i <= n;i++)g[i] = (!i+f[i]*I)%mod;ln(g,lng1,n);for(int i = 0;i <= n;i++)g[i] = jian(!i,f[i]*I%mod);ln(g,lng2,n);int mul = inv2*invI%mod;for(int i = 0;i <= n;i++)g[i] = (lng1[i]-lng2[i]+mod)*mul%mod;
}