226 翻转二叉树
func invertTree(root *TreeNode) *TreeNode {// 思考,广度优先遍历,对于每一层,翻转其左右子节点if root == nil {return nil}queue := list.New()queue.PushBack(root)size := 1 // 存储每一层的节点个数for queue.Len() > 0{var count intfor i:=0; i<size; i++{ // 弹出该层所有的节点node := queue.Remove(queue.Front()).(*TreeNode)// 将该节点的左右子节点翻转if node.Left != nil || node.Right != nil {node.Left, node.Right = node.Right, node.Left}// 将翻转后的子节点入队列if node.Left != nil {queue.PushBack(node.Left)count++}if node.Right != nil {queue.PushBack(node.Right)count++}}size = count}return root
}
// list双向链表实现的队列,插入移除操作复杂度都是1
// 所以时间 遍历翻转每一个节点 n 空间 队列 n
func invertTree(root *TreeNode) *TreeNode { // 递归参数返回值// 递归前序遍历if root == nil { // 递归终止条件return nil}// 交换左右子节点if root.Left != nil || root.Right != nil { // 单次递归逻辑root.Left, root.Right = root.Right, root.Left}invertTree(root.Left)invertTree(root.Right)return root
}
// 时间复杂度n 空间 如果平衡二叉树logn 如果链表 n
// 递归前序后序遍历都可以直观理解,但是中序时候,需要特殊处理递归逻辑,因为先一步递归左子树之后,处理完交换逻辑左子树变成了右子树,此时往下执行交换右子树就是错误的,所以之后的逻辑应该改成仍然交互左子树
101 判断二叉树对称
func isSymmetric(root *TreeNode) bool {// 递归if root == nil {return true}return symmetric(root.Left, root.Right)
}func symmetric(left, right *TreeNode) bool { // 递归参数返回值// 递归终止条件if left == nil && right != nil ||left != nil && right == nil ||left != nil && right != nil && left.Val != right.Val {// 左空右非空 || 左非空右边空 || 左右数值不相等return false}if left == nil && right == nil {return true}// 最后一种情况,左右非空并且值相等// 递归逻辑inner := symmetric(left.Left, right.Right)outer := symmetric(left.Right, right.Left)return inner && outer
}时间,每个节点遍历一次 n 空间logn
104 最大深度
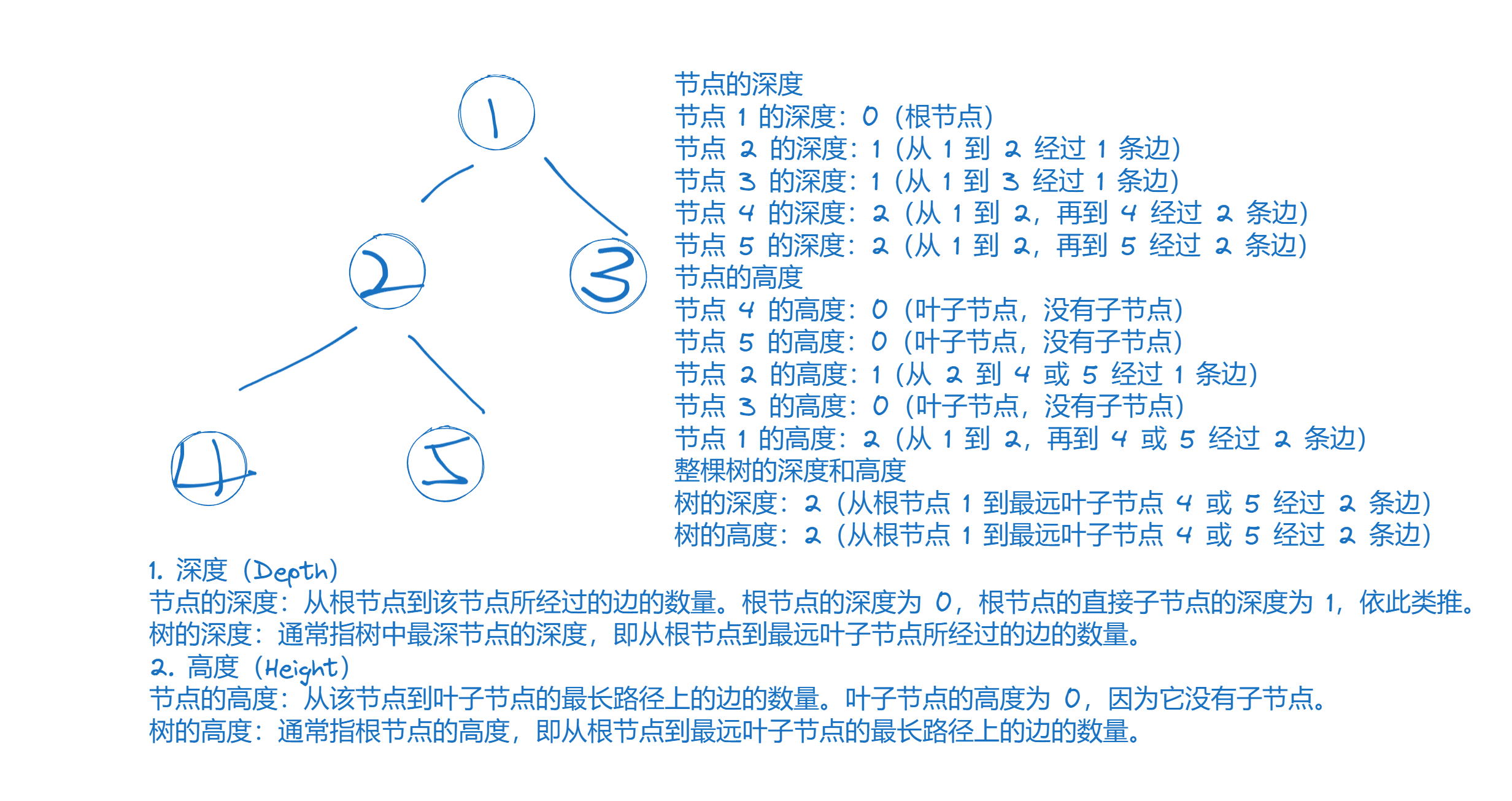
func maxDepth(root *TreeNode) int {// 考虑层序遍历if root == nil {return 0}queue := list.New()queue.PushBack(root)dep := 1size := 1for queue.Len() >0{var count intfor i:=0; i<size; i++ {node := queue.Remove(queue.Front()).(*TreeNode)if node.Left != nil {queue.PushBack(node.Left)count++}if node.Right != nil {queue.PushBack(node.Right)count++}}if count == 0{return dep}size = countdep++}return dep
}
// 层序遍历每个节点遍历一次,时间n 空间 队列长度最长为n/2 = n
func maxDepth(root *TreeNode) int {// 递归方法,深度优先遍历,因为需要不断传递子节点高度给父节点,所以考虑后续遍历,同时根节点高度就是树的深度if root == nil {return 0}left := maxDepth(root.Left)right := maxDepth(root.Right)var res int = rightif left > right {res = left}return res+1
}
111 最小深度
func minDepth(root *TreeNode) int {// 思考层序遍历,终止条件是左右子树都是空if root == nil {return 0}queue := list.New()queue.PushBack(root)dep := 1size := 1for queue.Len() >0 {var count intfor i := 0; i < size; i++ {node := queue.Remove(queue.Front()).(*TreeNode)if node.Left == nil && node.Right == nil {return dep}if node.Left != nil {queue.PushBack(node.Left)count++}if node.Right != nil {queue.PushBack(node.Right)count++}}size = countdep++}return dep
}
// 层序遍历每个节点遍历一次,时间n 空间 队列长度最长为n/2 = n
func minDepth(root *TreeNode) int {// 递归方法,深度优先遍历,最小深度,终止条件是遇到无叶子的子节点,从上往下传递,中左右前序遍历if root == nil {return 0}// 如果左子树为空,递归右子树if root.Left == nil {return minDepth(root.Right) + 1}// 如果右子树为空,递归左子树if root.Right == nil {return minDepth(root.Left) + 1}// 左右子树都不为空,返回左右子树的最小深度leftDepth := minDepth(root.Left)rightDepth := minDepth(root.Right)return int(math.Min(float64(leftDepth), float64(rightDepth))) + 1
}