lca
lca简称最近公共祖先——简介在此,不过多赘述
这里主要写的是倍增算法,oi-wiki上用的是vector,由于本人不会,只会用链表,所以这里就放链表的代码了
例题
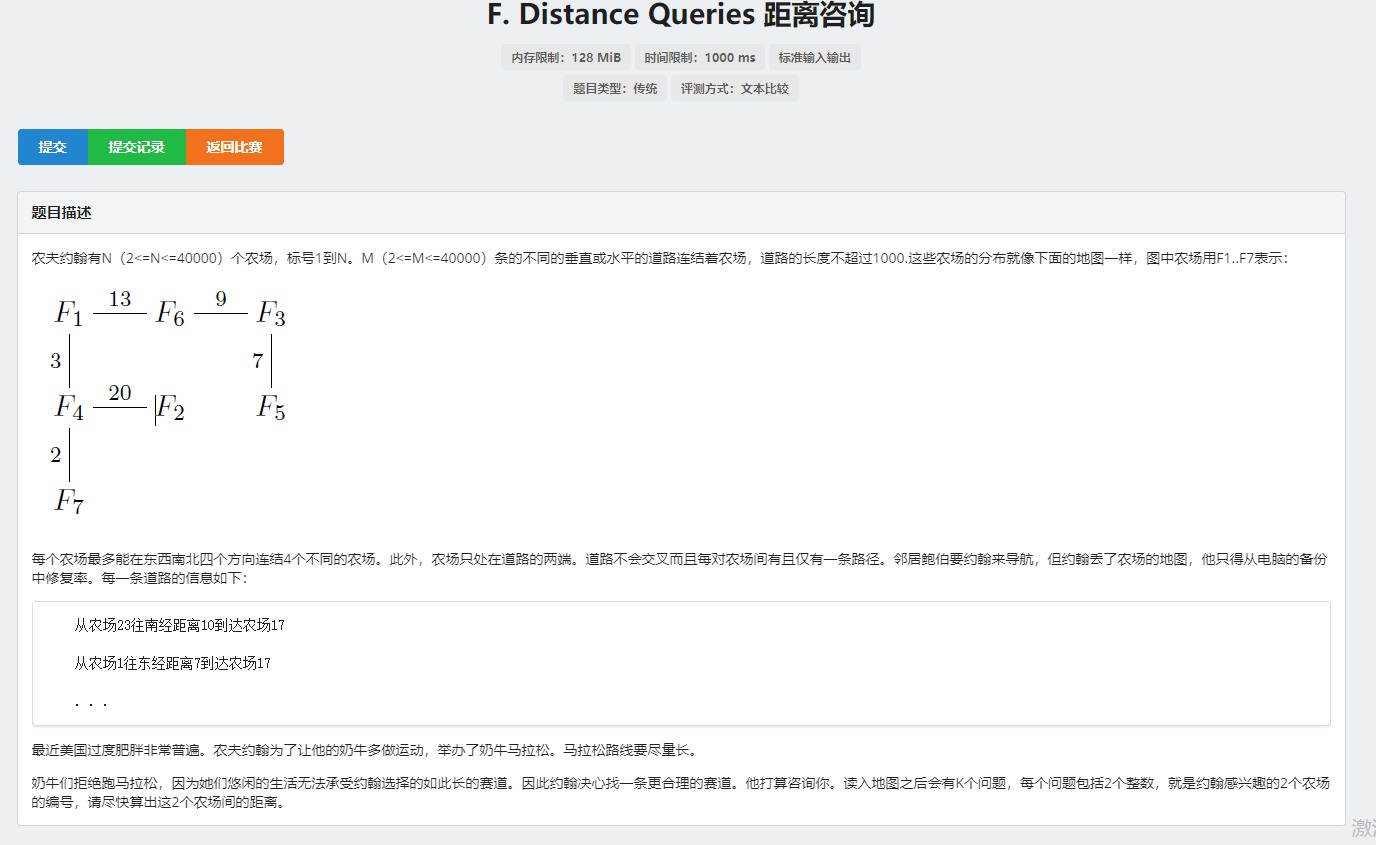
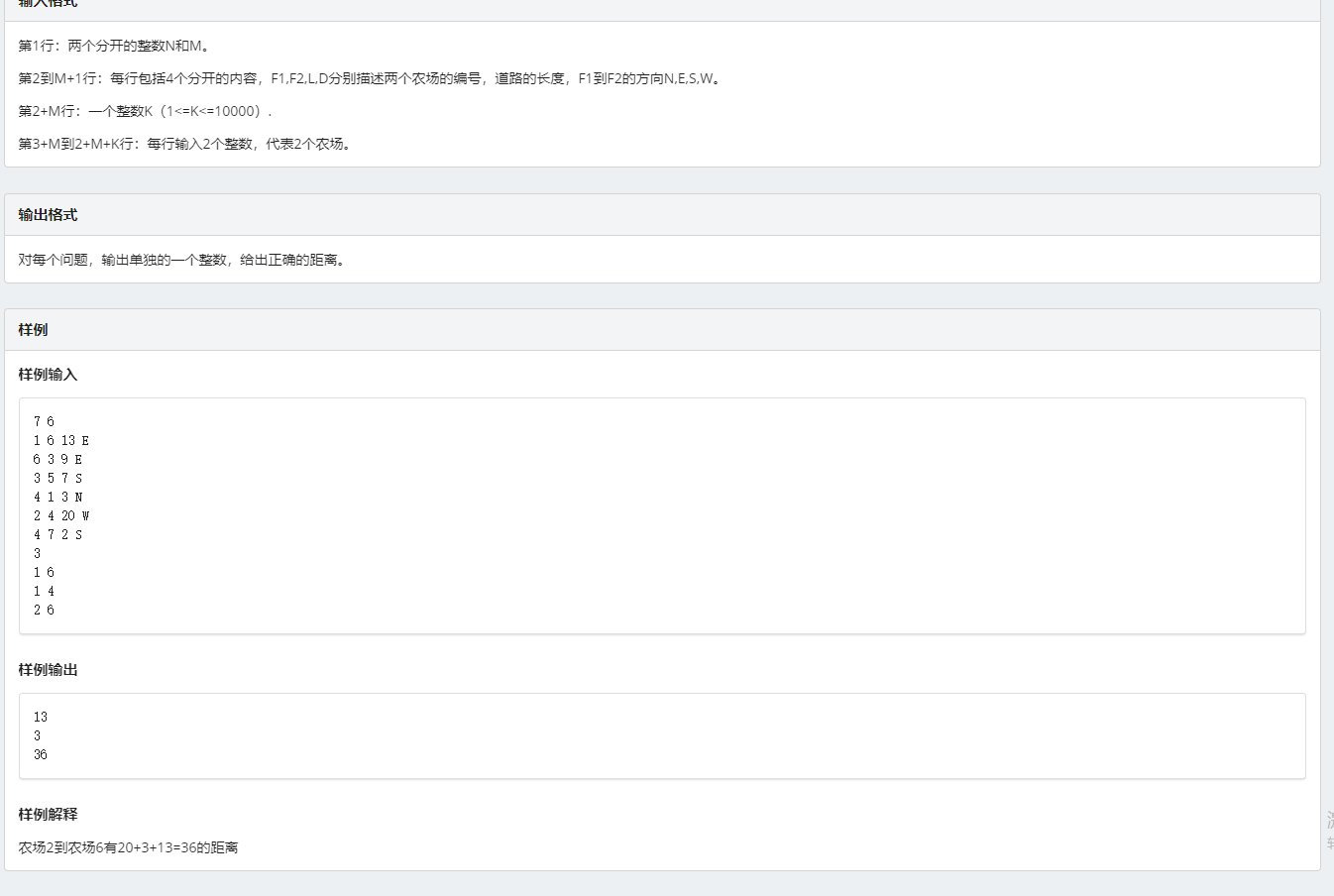
加一个数组按倍增数组的方式存距离即可
题解——点击查看代码
#include<bits/stdc++.h>
#define int long long
const int maxn=1e6+10;
using namespace std;
int n,m,root,nxt[maxn<<2],to[maxn<<2],head[maxn<<2],tot,val[maxn<<2];
int cnt,dep[maxn<<2],f[maxn][20],dis[maxn][20];
void add(int x,int y,int z)
{to[++tot]=y;val[tot]=z;nxt[tot]=head[x];head[x]=tot;
}
void dfs(int u,int fa,int dist)
{dis[u][0]=dist;f[u][0]=fa;dep[u]=dep[fa]+1;for(int i=1;(1<<i)<=dep[u];i++){f[u][i]=f[f[u][i-1]][i-1];dis[u][i]=dis[u][i-1]+dis[f[u][i-1]][i-1];} for(int i=head[u];i;i=nxt[i]){int y=to[i];if(y==fa) continue;dfs(y,u,val[i]);}
}
int lca(int x,int y)
{int res=0;if(dep[x]<dep[y]) swap(x,y);for(int i=17;i>=0;i--){if(dep[y]+(1<<i)<=dep[x]) res+=dis[x][i],x=f[x][i]; }if(x==y) return res;for(int i=17;i>=0;i--){if(f[y][i]!=f[x][i]){res+=dis[x][i];res+=dis[y][i];x=f[x][i];y=f[y][i];}}return dis[x][0]+dis[y][0]+res;
}signed main()
{scanf("%d%d",&n,&m);char aa[2];int x,y,z;for(int i=1;i<=m;i++){scanf("%lld%lld%lld %s ",&x,&y,&z,&aa[1]);add(x,y,z);add(y,x,z);} dfs(1,0,0);int k;scanf("%lld",&k); for(int i=1;i<=k;i++){scanf("%lld%lld",&x,&y);printf("%lld\n",lca(x,y));}return 0;
}
树上差分
主要用途是在树上的一些统计计数操作,对树上两点路径的操作用的
主要思想
dfs深搜实现,在两端结点计数,在深搜回溯时把计数的操作从子节点传递到父节点,用下面这个图理解一下
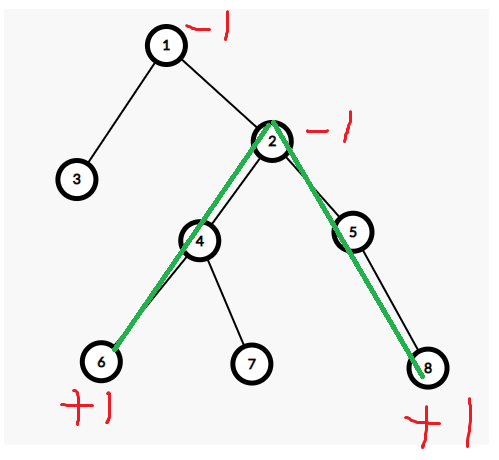
假设我们有这样一张图,我们要在6和8两个节点间的路径加一,那我们在用树上差分时,在两端+1,会发现它们的最近公共
祖先2及以上祖先都加了2,我们的目的是让2加1,2的祖先不变,则我们需要在2处减一,2的父亲处再减一即可
例题在此
题解
#include<bits/stdc++.h>
#define int long long
const int maxn=1e6+10;
using namespace std;
int n,m,root,head[maxn<<2],tot,sum;
int cnt,dep[maxn<<2],f[maxn][21],tg[maxn],a[maxn];
bool vis[maxn<<2];
struct tree{int to,val,nxt;}e[maxn<<2];
void add(int x,int y)
{e[++tot].to=y;e[tot].nxt=head[x];head[x]=tot;
}void dfs1(int u,int fa)
{vis[u]=1;for(int i=1;(1<<i)<=dep[u];i++){f[u][i]=f[f[u][i-1]][i-1];}for(int i=head[u];i;i=e[i].nxt){int y=e[i].to;if(vis[y]||y==fa) continue;f[y][0]=u;dep[y]=dep[u]+1;dfs1(y,u);}
}int lca(int x,int y)
{if(dep[x]<dep[y]) swap(x,y);for(int i=20;i>=0;i--){if(dep[x]>=dep[y]+(1<<i)) x=f[x][i];}if(x==y) return x;for(int i=20;i>=0;i--){if(f[x][i]!=f[y][i]){x=f[x][i];y=f[y][i];}}return f[x][0];
}void dfs(int u)
{vis[u]=1;for(int i=head[u];i;i=e[i].nxt){int y=e[i].to;if(vis[y])continue;dfs(y);tg[u]+=tg[y];}
}signed main()
{scanf("%lld",&n);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);} int x,y;for(int i=1;i<n;i++){scanf("%lld%lld",&x,&y);add(x,y);add(y,x); } dfs1(1,0);for(int i=1;i<n;i++){tg[a[i]]++;tg[a[i+1]]++;tg[ lca(a[i],a[i+1]) ]--;tg[f[ lca(a[i],a[i+1]) ][0]]--;/*en~~,神奇的东西,相邻的加1,但从a[2]到a[3]时a[2]不用加1,这就导致除了首尾糖果都 多加了1,但到最后一个糖果时不用拿,所以只有第一个位置的糖果是对的所以让第一个糖果数加1,最后输出时都减一就好了 */ }memset(vis,0,sizeof vis);dfs(1);tg[a[1]]++; for(int i=1;i<=n;i++) printf("%lld\n",tg[i]-1);return 0;
}拓展
1.求树上一点走k步可以走到的点的个数
将其 \(k\) 级祖先内的点加 \(1\) 用树上差分可以实现,这里再加一种更简便的思路
\(dfs\) 一遍,维护一个栈,进一个点时记一下数量,回溯时再记一下数量,回溯是把距离超过 \(k\) 的点从栈中删了
这里记的两个数量差就是 \(k\) 步可以走到的。复杂度 \(O(n)\)
点击查看代码
void dfs(int &num,int x,int fa,int d)
{int t=num;if(d>top)st[++top]=0;num++,st[d]++;for(int i=head[x];i;i=nxt[i]){int y=to[i];if(y==fa)continue;dfs(num,y,x,d+1);}ans[x]=num-t;if(top==d+k) num-=st[top--];
}
2.环上差分
环上差分需要先找环,适用于环上的点对一段区间有影响问题
floyd找环法
while(u!=y&&u!=to[y])u=to[u],y=to[to[y]];
环上差分和树上差分差不多,都是信息一步一步向上传来统计的
例题在此
题解
#include<bits/stdc++.h>
const int maxn=5e5+10;
using namespace std;
int n,k,tot,head[maxn],to[maxn],nxt[maxn],v[maxn];
int st[maxn],top,ans[maxn],a[maxn],cnt,s[maxn];void add(int x,int y)
{to[++tot]=y;nxt[tot]=head[x];head[x]=tot;
} void dfs(int &num,int x,int fa,int d)
{
// cout<<x<<" "<<fa<<" "<<d<<endl;int t=num;if(d>top)st[++top]=0;num++,st[d]++;for(int i=head[x];i;i=nxt[i]){int y=to[i];if(y==fa)continue;dfs(num,y,x,d+1);}ans[x]=num-t;if(top==d+k) num-=st[top--];
}
inline int mo(int i,int x){return i+x<=cnt?i+x:i+x-cnt;}
void solve(int x)
{int u=x,y=v[x];while(u!=y&&u!=v[y])u=v[u],y=v[v[y]];a[cnt=1]=u;for(int i=v[u];i!=u;i=v[i])a[++cnt]=i;
// for(int i=1;i<=cnt;i++)s[i]=0;fill(s+1,s+cnt+1,0);int sum=min(k+1,cnt);
// cout<<cnt<<" !"<<endl;for(int i=1;i<=cnt;i++){for(int j=head[a[i]];j;j=nxt[j]){int y=to[j];if(y==a[mo(i,cnt-1)])continue;int num=0;st[top=0]=0;dfs(num,y,a[i],1);for(int d=1;d<=top;d++){int temp=st[d];if(k-d>=cnt)sum+=temp;else{int m=mo(i,k-d+1);s[i]+=temp,s[m]-=temp;if(m<=i) s[1]+=temp;}} }}for(int i=1;i<=cnt;i++) sum+=s[i],ans[a[i]]=sum;
}int main()
{ios::sync_with_stdio(0);cin.tie(0),cout.tie(0); cin>>n>>k;for(int i=1;i<=n;i++){int x;cin>>x;add(x,i);v[i]=x;
// ans[i]=-1;}fill(ans+1,ans+1+n,-1);for(int i=1;i<=n;i++) if(ans[i]==-1) solve(i);for(int i=1;i<=n;i++)cout<<ans[i]<<'\n';return 0;
}
/*
6 2
2
3
4
5
4
3
*/
你已完成新手教程,下面开启困难模式
树上差分计数变形
题目在此
题解——二分加树上差分
#include<bits/stdc++.h>
const int maxn=1e6+10;
using namespace std;
int n,m,root,head[maxn],tot,a[maxn],b[maxn];
int cnt,dep[maxn],f[maxn][21],dis[maxn][21],sum[maxn],l,r,ans;
bool vis[maxn];
struct tree{int to,val,nxt;}e[maxn<<2];
struct node{int a,b,anc,val;}le[maxn<<2]; void add(int x,int y,int z)
{e[++tot].to=y;e[tot].nxt=head[x];e[tot].val=z;head[x]=tot;
}void dfs(int u,int fa)
{vis[u]=1;for(int i=1;(1<<i)<=dep[u];i++){f[u][i]=f[f[u][i-1]][i-1]; dis[u][i]=dis[u][i-1]+dis[f[u][i-1]][i-1];}for(int i=head[u];i;i=e[i].nxt){int y=e[i].to;if(vis[y]||y==fa) continue;f[y][0]=u;b[y]=i;dis[y][0]=e[i].val;dep[y]=dep[u]+1;dfs(y,u);}
}int lca(int x,int y)
{if(dep[x]>dep[y]) swap(x,y);for(int i=20;i>=0;i--){if(dep[x]+(1<<i)<=dep[y]) y=f[y][i]; }if(x==y) return y;for(int i=20;i>=0;i--){if(f[y][i]!=f[x][i]){x=f[x][i];y=f[y][i];}}return f[y][0];
}int solve(int x,int y)
{int res=0;if(dep[x]<dep[y])swap(x,y);for(int i=17;i>=0;i--){if(dep[x]>=dep[y]+(1<<i)) res+=dis[x][i],x=f[x][i];}if(x==y)return res;for(int i=17;i>=0;i--){if(f[y][i]!=f[x][i]){res+=dis[x][i]+dis[y][i];x=f[x][i];y=f[y][i];}}return dis[x][0]+dis[y][0]+res;
}void update(int now,int fa)
{for(int i=head[now];i;i=e[i].nxt){if(e[i].to!=fa){update(e[i].to,now);sum[now]+=sum[e[i].to];}}
}bool check(int x)
{int cnt=0,dec=0;memset(sum,0,sizeof sum);for(int i=1;i<=n;i++){if(le[i].val>x){cnt++;sum[le[i].a]++;sum[le[i].b]++;sum[le[i].anc]-=2;dec=max(dec,le[i].val-x);}}update(1,1);for(int i=1;i<=n;i++)if(sum[i]==cnt&&e[b[i]].val>=dec) return 1;return 0;
}int main()
{scanf("%d%d",&n,&m);int x,y,z;for(int i=1;i<n;i++){scanf("%d%d%d",&x,&y,&z);add(x,y,z);add(y,x,z);}dfs(1,0);for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);le[i]={x,y,lca(x,y),solve(x,y)};r=max(r,le[i].val);} r++;while(l<r){int mid=(l+r)>>1;if(check(mid))ans=r=mid;else l=mid+1;}printf("%d",ans);return 0;
}
树上差分加线段树合并
题目在此
题解
#include<bits/stdc++.h>
#define lid m[id].ls
#define rid m[id].rs
const int maxn=1e5+10;
using namespace std;
int n,t,len,head[maxn],nxt[maxn<<1],to[maxn<<1],tot,cnt;
int rt[maxn],sum,s[maxn*80],ans[maxn];
struct node{int ls,rs,sum;}m[maxn*80];
int dep[maxn],f[maxn][21];inline void add(int x,int y)
{to[++cnt]=y;nxt[cnt]=head[x];head[x]=cnt;
}inline void addm(int x,int y)
{add(x,y);add(y,x);
}inline void push(int id)
{if(!lid){m[id].sum=m[rid].sum,s[id]=s[rid];return ;}if(!rid){m[id].sum=m[lid].sum,s[id]=s[lid];return ;} m[id].sum=max(m[lid].sum,m[rid].sum);s[id]=m[lid].sum>=m[rid].sum?s[lid]:s[rid];
}inline void merge(int &a,int b,int l,int r)
{if(!b) return;if(!a){ a=b;return ;}if(l==r){ m[a].sum+=m[b].sum;return ;}int mid=(l+r)>>1;merge(m[a].ls,m[b].ls,l,mid),merge(m[a].rs,m[b].rs,mid+1,r);push(a);
}inline void insert(int &id,int l,int r,int x,int y)
{if(!id)id=++tot;if(l==r){m[id].sum+=y;s[id]=x;return;}int mid=(l+r)>>1;if(x<=mid)insert(lid,l,mid,x,y);else insert(rid,mid+1,r,x,y);push(id);
} inline void dfs(int u,int fa)
{for(int i=1;(1<<i)<=dep[u];i++)f[u][i]=f[f[u][i-1]][i-1];for(int i=head[u];i;i=nxt[i]){int y=to[i];if(y==fa)continue;f[y][0]=u;dep[y]=dep[u]+1;dfs(y,u);}
} inline int lca(int x,int y)
{if(dep[x]<dep[y])swap(x,y);for(int i=20;i>=0;i--)if(dep[y]+(1<<i)<=dep[x])x=f[x][i];if(x==y)return x;for(int i=20;i>=0;i--){if(f[y][i]!=f[x][i]){x=f[x][i];y=f[y][i];}}return f[x][0];
}void as(int u,int fa)
{for(int i=head[u];i;i=nxt[i]){int y=to[i];if(y==fa)continue;as(y,u);merge(rt[u],rt[y],1,maxn-10);}ans[u]=s[rt[u]];if(!m[rt[u]].sum) ans[u]=0;
}int main(){scanf("%d%d",&n,&t);for(int i=1;i<n;i++){int x,y;scanf("%d%d",&x,&y);addm(x,y);} dfs(1,0);for(int i=1;i<=t;i++){int a,b,c,d; scanf("%d%d%d",&a,&b,&c);d=lca(a,b);insert(rt[a],1,maxn,c,1),insert(rt[b],1,maxn,c,1);insert(rt[d],1,maxn,c,-1);insert(rt[f[d][0]],1,maxn,c,-1); } as(1,0);for(int i=1;i<=n;i++)printf("%d\n",ans[i]);return 0;
}