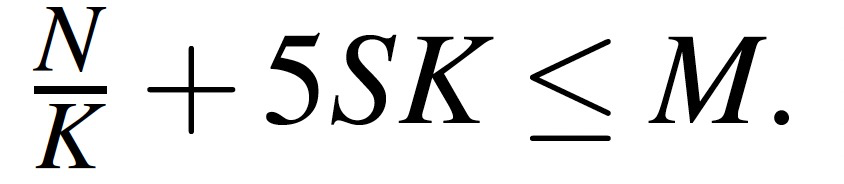?apj 你在干神魔
- W4terCTF 2024
- Merciful ZMJ4396
- d3
- Google CTF 2023
- LEAST COMMON GENOMINATOR
- DeadSec CTF 2024
- Raul Rosas
- corCTF 2024
- steps
- monkfish / anglerfish
W4terCTF 2024
之前朋友给我看的题
Merciful ZMJ4396
找不到原来的 task.py 了,记得大概是这么个题,口胡一下吧
有两个多项式 \(F(m) = m^{43} + 96, G(m) = (m-7)^{77} + (m+777)^7\),要你找到一个 \(m\),使得 \(\gcd(F(m), G(m)) > 2^{7777}\)
当时没做出来,后来看 wp 才大概看明白的
首先关于多项式 \(\gcd\) 有一些高深理论,我没太研究明白,反正大概就是有个东西叫结式(resultant),然后两个多项式的值的 \(\gcd\) 一定是这两个多项式的结式的因子,且结式的每个因子都一定可以被取到。好像通过一些对多项式做 exgcd 也能得到这个数?确实没有太研究明白就摆了,丢个 wikipedia 在这里吧。还有个关于 \(\gcd\) 值的 ref。
总而言之,对于这题来说,可以直接求一下 \(F(m)\) 和 \(G(m)\) 的结式,就能知道这两个多项式 \(\gcd\) 的最大值是多少了。设它为 \(P\),级别大概是 \(2^{9000}\) 多的。那么现在我们只需要找到能够取到它的 \(m\) 即可。当然这好像还是不太容易,因为这等价于解 \(F(m) \equiv 0 \pmod P\) 和 \(G(m) \equiv 0 \pmod P\) 的解集的交,但是光求一个高次方程的解已经不可接受了(\(P\) 太大了无法分解,所以很难做高次剩余),所以我们还需要考虑一些东西。
实际上我们可以找一下在模 \(P\) 意义下的 \(\gcd(F, G)\),这里是多项式的 \(\gcd\)。那么我们要的解就是 \(\gcd(F, G) \equiv 0 \pmod P\) 了。(我怎么没想到这个)但是发现模合数 \(\gcd\) 好像不一定存在,库直接没有这个的实现,那自己写一个朴素 \(\gcd\) 吧。发现确实找不到 \(\gcd\),因为没有逆元。尝试将 \(P\) 的比较小的因子除掉(\(2^{10} | P\)),然后发现就找到 \(\gcd\) 了,而且次数很小,是个一次多项式。这样直接就解出 \(m\) 了。
from sage.all import *
from gmpy2 import *def gcd1(a, b):if b == 0:return a.monic()else:return gcd1(b, a % b)PR = PolynomialRing(ZZ,'x')
x = PR.gen()
f = x ** 43 + 96
g = (x - 7) ** 77 + (x + 777) ** 7
P = abs(f.resultant(g))
print(P)
P //= 2 ** 10PR = PolynomialRing(Zmod(P),'x')
x = PR.gen()
f = x ** 43 + 96
g = (x - 7) ** 77 + (x + 777) ** 7
h = gcd1(f, g)
print(h)
# h's degree = 1
m = gmpy2.mpz(P - h[0])
ans = gmpy2.gcd(m ** 43 + 96, (m - 7) ** 77 + (m + 777) ** 7)print(ans.bit_length())print(m)
d3
好像是叫这个???我忘了,同样是找不到 task.py,数据范围也不咋记得了,直接口胡了,我只记得当时我做法是对的但是有些细节弱智了导致掉了大量精度,结果最后跑不出来答案
给你一个数 \(d\) 的立方根的小数部分,还原 \(d\)。
小数部分大概是给到了 \(2^{-1024}\) 的精度?记不太清了。
设整数部分为 \(x\),小数部分为 \(y\),那么 \(\sqrt[3]{d} = x + y\),我们知道 \(y\),现在相当于要找 \(x\)。
我们知道的信息应当是 \((x + y)^3 \equiv 0 \pmod 1\),拆一下有 \(x^3 + 3x^2y + 3xy^2 + y^3 \equiv 0 \pmod 1\)。注意到 \(x\) 是整数,所以实际上限制是 \(3x^2y + 3xy^2 + y^3 \equiv 0 \pmod 1\)。\(y^3\) 是一个已知数,我们现在相当于要解一个关于 \(x\) 的二次方程。但是当然要注意到我们这里的精度是有限的,所以我们实际上要做的是找到一个近似解。
首先把浮点数干掉,我们左右同时乘上一个大数 \(A\),大概 \(2^{2048}\),取整一下,然后就可以得到一个整数的问题了。(有个傻逼先把 \(y\) 取整之后再求三次方,然后精度炸的不剩了,不说是谁)现在问题就是求 \(Px^2 + Qx + R \equiv 0 \pmod A\) 了。注意我们可以大概预估 \(x\) 的大小应该在 \(2^{300}\) 级别。这个二次很火大啊,我们考虑直接把 \(x^2\) 和 \(x\) 独立开,令 \(z = x^2\),然后假设 \(z\) 是一个 \(2^{600}\) 级别的变量,直接跑跑看。然后这就是一个标准形式的线性同余了,可以直接上格基 LLL 了。不会的可以看看 WC 2024 游记(
我手头没代码,懒得写了!
Google CTF 2023
LEAST COMMON GENOMINATOR
ok 这题是当时闲的没事做的。来试试自己能不能做出来 google ctf 的 crypto 签到题(
但是好像也错过了 google ctf 2024,哈哈
task.py
题目大概是给了一个 LCG,你不知道它的系数,然后给出了前 6 个生成的数,然后用这个 LCG 生成了 RSA 的 key,我们的目标就是通过这 6 个生成的数还原出来这个 LCG 的系数。
LCG:\(x_i = (x_{i-1} \cdot m + c) \bmod n\)
给出了 \(x_1 \sim x_6\),我们可以先差分一下,\(x_{i+1} - x_{i} = m(x_{i} - x_{i-1})\),令 \(y_i = x_{i+1} - x_i\),那么 \(y_i\) 实际上是形成了一个等比数列,\(y_i = y_{i-1} \cdot m\)。但是我们现在即不知道比也不知道模数。
考虑相邻两组,假设为 \(y_3 = y_2 m + t_2 n, y_2 = y_1 m + t_1 n\),可以将 \(m\) 消去,得到 \(y_3 y_1 - t_2 y_1 n = y_1 y_2 m = y_2^2 - t_1 y_2 n\),那么就有 \((t_1 y_2 - t_2 y_1) n = y_2^2 - y_3 y_1\),这实际上告诉了我们 \(n\) 一定是 \(y_2^2 - y_3 y_1\) 的因子,而我们有 4 组这样的方程,将所有的 \(y_2^2 - y_3 y_1\) 求一下 \(\gcd\) 就能还原出来 \(n\) 了,然后就容易解出整个 LCG 了。
代码还是没有,太久之前做的题了现在没有代码了!
DeadSec CTF 2024
ok 这个是最近打的了。

有点菜!crypto 被卡了两题,虽然最后看题解发现是傻逼题,两题我想法都是对的但是一个我算的理论不可行一个我跑到一半放弃了。那两个题不写了,感觉真没意思。
Raul Rosas
task.py:
from Crypto.Util.number import * from sympy import nextprimep1 = bin(getPrime(1024))[2:] p2 = p1[:605] p2 = p2 + ('0'*(len(p1)-len(p2)))p1 = int(p1,2) p2 = nextprime(int(p2,2))q1 = getPrime(300) q2 = getPrime(300)n1 = p1*p1*q1 n2 = p2*p2*q2 e = 65537 flag = bytes_to_long(b'REDACTED') c1 = pow(flag,e,n1) c2 = pow(flag,e,n2)print(f'{n1=}') print(f'{n2=}') print(f'{c1=}') print(f'{c2=}')
这个题对于 OIer 还是不太难的吧!虽然我做法可能有点偏,正解可能不是这个(
代码里 \(p_1\) 是一个随机数,\(p_2\) 是一个和 \(p_1\) 很接近的质数,\(q_1, q_2\) 是两个随机质数。然后给出了同一个 flag 的两次 RSA 加密,模数 \(n_1 = p_1^2 q_1, n_2 = p_2^2 q_2\)。由于我们知道 \(p_1\) 和 \(p_2\) 相差很小,那么 \(\frac{n_1}{n_2}\) 约等于 \(\frac{q_1}{q_2}\),而且我们知道 \(q_1, q_2\) 的位数,我们直接找到一个 \(\frac{n_1}{n_2}\) 的最近有理逼近即可。我写的是 Stern-Broot 树上朴素二分,比较简单。
from Crypto.Util.number import *
from sympy import nextprime
from decimal import *
getcontext().prec = 1024n1 = 33914684861748025775039281034732118800210172226202865626649257734640860626122496857824722482435571212266837521062975265470108636677204118801674455876175256919094583111702086440374440069720564836535455468886946320281180036997133848753476194808776154286740338853149382219104098930424628379244203425638143586895732678175237573473771798480275214400819978317207532566320561087373402673942574292313462136068626729114505686759701305592972367260477978324301469299251420212283758756993372112866755859599750559165005003201133841030574381795101573167606659158769490361449603797836102692182242091338045317594471059984757228202609971840405638858696334676026230362235521239830379389872765912383844262135900613776738814453
n2 = 45676791074605066998943099103364315794006332282441283064976666268034083630735700946472676852534025506807314001461603559827433723291528233236210007601454376876234611894686433890588598497194981540553814858726066215204034517808726230108550384400665772370055344973309767254730566845236167460471232855535131280959838577294392570538301153645042892860893604629926657287846345355440026453883519493151299226289819375073507978835796436834205595029397133882344120359631326071197504087811348353107585352525436957117561997040934067881585416375733220284897170841715716721313708208669285280362958902914780961119036511592607473063247721427765849962400322051875888323638189434117452309193654141881914639294164650898861297303
c1 = 5901547799381070840359392038174495588170513247847714273595411167296183629412915012222227027356430642556122066895371444948863326101566394976530551223412292667644441453331065752759544619792554573114517925105448879969399346787436142706971884168511458472259984991259195488997495087540800463362289424481986635322685691583804462882482621269852340750338483349943910768394808039522826196641550659069967791745064008046300108627004744686494254057929843770761235779923141642086541365488201157760211440185514437408144860842733403640608261720306139244013974182714767738134497204545868435961883422098094282377180143072849852529146164709312766146939608395412424617384059645917698095750364523710239164016515753752257367489
c2 = 3390569979784056878736266202871557824004856366694719533085092616630555208111973443587439052592998102055488632207160968490605754861061546019836966349190018267098889823086718042220586285728994179393183870155266933282043334755304139243271973119125463775794806745935480171168951943663617953860813929121178431737477240925668994665543833309966378218572247768170043609879504955562993281112055931542971553613629203301798161781786253559679002805820092716314906043601765180455118897800232982799905604384587625502913096329061269176369601390578862509347479694697409545495592160695530037113884443071693090949908858172105089597051790694863761129626857737468493438459158669342430468741236573321658187309329276080990875017e = 65537# find approximation of n1/n2l = (0, 1)
r = (1, 0)def check(q1, q2):if q1 != 1 and n1 % q1 == 0 and n2 % q2 == 0:print(q1, q2)p2 = int(Decimal(n2 // q2).sqrt())d = inverse(e, (p2 - 1) * p2 * (q2 - 1))m = pow(c2, d, n2)print(long_to_bytes(m))while l[1] < 2 ** 300 and r[1] < 2 ** 300:mid = (l[0] + r[0], l[1] + r[1])check(mid[0], mid[1])if mid[0] * n2 < n1 * mid[1]:l = midelse:r = mid
corCTF 2024
这个是在上一场 ctf 被那两题卡自闭之后弃赛来打的这场。

彩笔队友这场 pwn 和 web 一题没过,要不然还能再多点分)
steps
task.py:
from Crypto.Util.number import getPrime from random import randint from hashlib import sha512 from secret import FLAGp = getPrime(1024)def apply(x, y):z0 = x[0] * y[1] + x[1] * y[0] - x[0] * y[0]z1 = x[0] * y[0] + x[1] * y[1]return z0 % p, z1 % pdef calculate(n):out = 0, 1base = 1, 1while n > 0:if n & 1 == 1: out = apply(out, base)n >>= 1base = apply(base, base)return outdef step(x, n):'''Performs n steps to x.'''return apply(x, calculate(n))def xor(a, b):return bytes(i ^ j for i, j in zip(a, b))g = tuple(randint(0, p - 1) for _ in range(2)) a = randint(0, p) b = randint(0, p)A = step(g, a) B = step(g, b)print(p) print(g) print(A) print(B)shared = step(A, b) assert shared == step(B, a)pad = sha512(str(shared).encode()).digest() print(xor(FLAG, pad))
注意到 他实际上写了个斐波那契数列,,,反正把转移矩阵写出来发现就是个斐波那契
那么实际上是给出了 \(g A^n\) 和 \(g A^m\),可以直接解方程解出来 \(f_n, f_{n-1}\) 和 \(f_m, f_{m-1}\),然后求 \(f_{n+m}\) 即可,可以用一下 \(f_{n+m} = f_n f_{m+1} + f_{n-1} f_{m}\),不太重要,随便算一下。
monkfish / anglerfish
task.py 太长了,不贴了
没看懂这题想干啥,,,有点搞笑,还分了两题
题目里给出了一个看起来很复杂的线性代数的算法,但是实际上都不重要,因为我们关注一下 \(verify(v, F, pok = (com, resp, verif))\) 函数,大概是用输入的 \((com, v, verif)\) 三元组为随机数种子随机一个 \(a\),然后判断 \(apply(F, resp) = com + a^2 v - a \cdot verif\)。但是所有数都是 \(\bmod 5\),意味着实际上 \(a\) 是可能随机到 \(0\) 的,而如果 \(a = 0\) 的时候这个判断条件是很容易满足的,只需要 \(com = apply(F, resp)\),而 \(com, resp\) 都是我们输入的,只需要随机一个 \(resp\) 并确定对应的 \(com\),为了随机到 \(a=0\) 我们一直对 \(verif\) 进行随机就行了。
#!/usr/bin/sageimport sys
print("I caught a monkfish in the sea! ")
sys.stdout.flush()from hashlib import sha256
from Crypto.Util.number import bytes_to_long
from random import SystemRandom
import astn = 100
m = 100
q = 5
FF.<x> = GF(q)def apply(F, v):out = []for i in range(m):out.append((v.T * F[i] * v)[0, 0])return matrix(FF, m, 1, out)def apply_verif_info(F, a, b):out = []for i in range(m):out.append((a.T * (F[i] + F[i].T) * b)[0, 0])return matrix(FF, m, 1, out)def create_pok(v, s, F):t = matrix(FF, n, 1, [FF.random_element() for i in range(n)])com = apply(F, t)verif = apply_verif_info(F, t, s)a = list(FF)[sha256(bytes([list(FF).index(i[0]) for i in list(com) + list(v) + list(verif)])).digest()[0] % len(list(FF))]print("a =", a)return (com, t - a * s, verif)def verif_pok(v, F, pi):com = pi[0]resp = pi[1]verif = pi[2]a = list(FF)[sha256(bytes([list(FF).index(i[0]) for i in list(com) + list(v) + list(verif)])).digest()[0] % len(list(FF))]out1 = apply(F, resp)out2 = com + (a * a) * v - a * verifreturn out1 == out2gen_seed = bytes([83, 134, 8, 60, 109, 129, 153, 246, 112, 132, 154, 0, 129, 173, 49, 229, 71, 79, 145, 91, 146, 44, 34, 251, 95, 41, 13, 248, 24, 126, 215, 95, 208, 88, 24, 74, 224, 166, 19, 232, 254, 0, 142, 215, 146, 93, 87, 249, 239, 253, 137, 92, 124, 201, 164, 4, 133, 176, 76, 70, 166, 193, 68, 148])F = []for i in range(m):cur = []for j in range(n):cur.append([])for k in range(n):cur[-1].append(list(FF)[sha256(gen_seed).digest()[0] % len(list(FF))])gen_seed = sha256(gen_seed).digest()F.append(matrix(FF, n, n, cur))vl = [2, 0, 3, 2, 4, 2, 4, 1, 4, 3, 4, 1, 1, 1, 2, 0, 4, 3, 4, 0, 0, 0, 0, 3, 2, 2, 3, 2, 0, 1, 1, 4, 2, 3, 4, 2, 4, 4, 2, 0, 1, 0, 1, 3, 4, 0, 0, 1, 0, 3, 4, 3, 0, 3, 4, 1, 1, 4, 1, 3, 0, 1, 4, 1, 2, 2, 2, 3, 2, 2, 4, 2, 4, 3, 0, 0, 3, 1, 4, 2, 1, 2, 1, 3, 2, 3, 4, 4, 4, 0, 1, 1, 2, 2, 1, 4, 3, 0, 2, 4]v = matrix(FF, n, 1, [list(FF)[i] for i in vl])m1 = random_matrix(FF, n, 1)
m0 = apply(F, m1)
while True:m2 = random_matrix(FF, n, 1)a = sha256(bytes([list(FF).index(i[0]) for i in list(m0) + list(v) + list(m2)])).digest()[0] % len(list(FF))print("a =", a)if a == 0:pi = (m0, m1, m2)res = verif_pok(v, F, pi)assert res == Trueprint([list(FF).index(i[0]) for i in list(m0)])print([list(FF).index(i[0]) for i in list(m1)])print([list(FF).index(i[0]) for i in list(m2)])exit()