P3043 [USACO12JAN] Bovine Alliance G 题解

P3043 [USACO12JAN] Bovine Alliance G

题目传送门

思路

首先分情况讨论每种联通块的可能，有三种不同的情况会对答案 \(ans\) 产生不同的贡献。

联通块有环

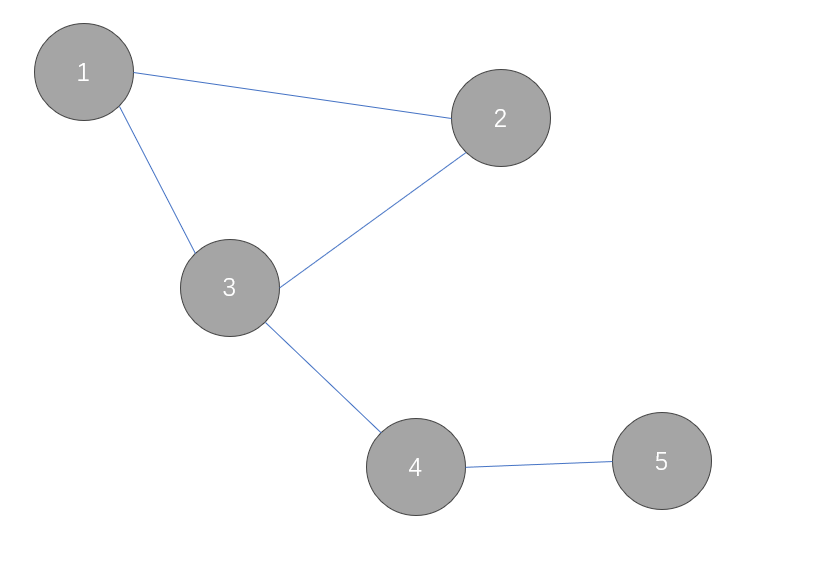
如图，因为每条边都有要有归属，所以环上的边只能全都顺时针或逆时针属于某个点，且不在环上的点仅有一种可能。

因此该情况对答案的贡献为 \(ans \times 2\) 。

联通块为链

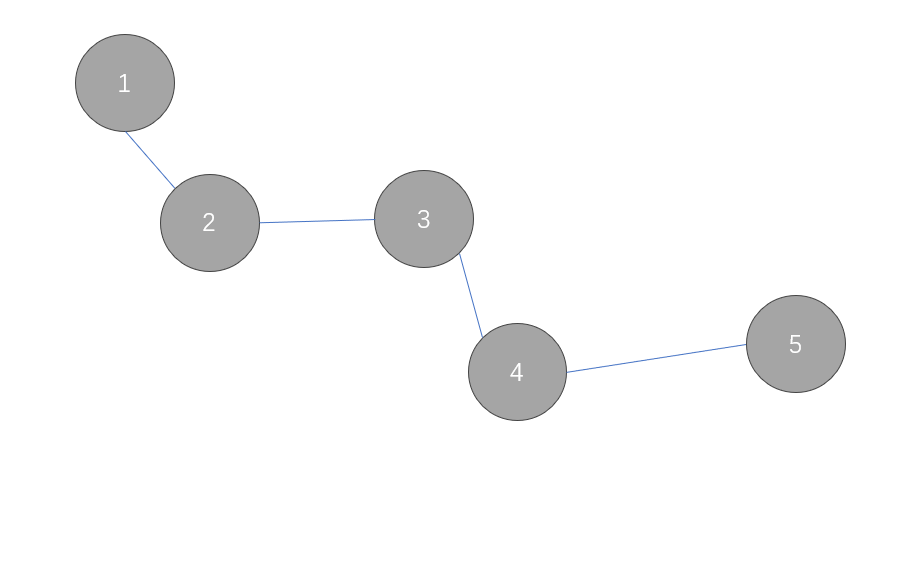
对于一条链，边数比点数小 1 所以仅有一个点是没有边的，而若确认某个点没有边的话，边的所属仅有一种可能。因此答案的贡献为 \(ans \times t\) ， \(t\) 为该联通块点的个数。

联通块内边数大于等于点数

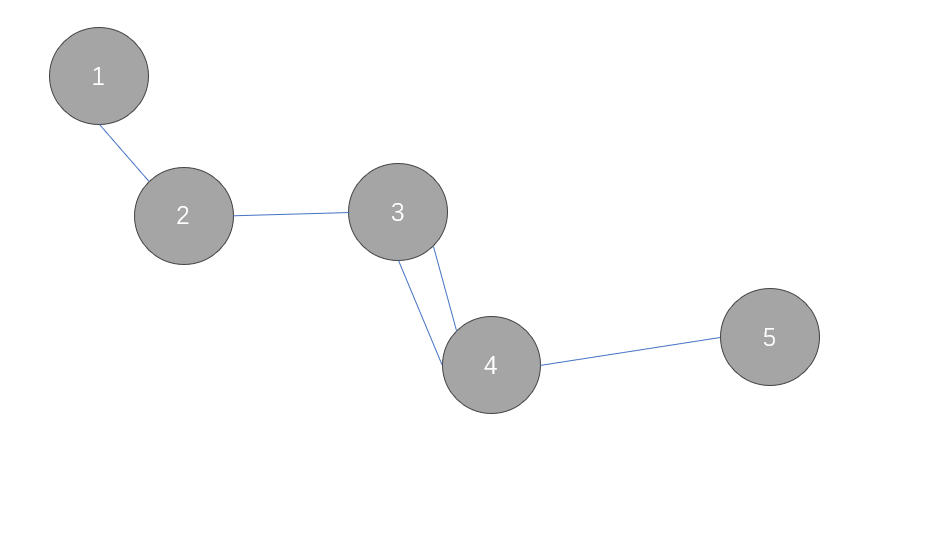
问题的答案为 \(0\) ，直接结束了。

转化

问题变为判断联通块内的情况，对此，利用联通块内度数除以 \(2\) 等于边数，判断点数与边数的关系即可。

代码

#include <iostream>
#include <cstdio>
typedef long long LL;using namespace std;const int mod = 1e9 + 7, N = 1e5 + 5;#define MOD(x) ((x + mod) % mod)
#define LF(i, __l, __r) for (int i = __l; i <= __r; i++)
#define RF(i, __r, __l) for (int i = __r; i >= __l; i--)int head[N], ver[N * 2], nxt[N * 2], edge[N * 2];
int n, m, tot = 1;
bool vis[N];
LL ans = 1, cnt, cnt1;void add(int u, int v) {ver[++tot] = v;nxt[tot] = head[u], head[u] = tot;
}void dfs(int u) {vis[u] = true, cnt++;for (int i = head[u]; i; i = nxt[i]) {cnt1++;if (!vis[ver[i]]) dfs(ver[i]);}
}int main() {scanf("%d%d", &n, &m);LF(i, 1, m) {int x, y;scanf("%d%d", &x, &y);add(x, y), add(y, x);}LF(i, 1, n) {if (!vis[i]) {cnt = cnt1 = 0;dfs(i);if (cnt == cnt1 / 2) ans = MOD(ans * 2);else if (cnt > cnt1 / 2) ans = MOD(ans * cnt);else { ans = 0; break; } }}printf("%lld", ans);return 0;
}

三军可夺帅也，匹夫不可夺志也。