2024暑假集训测试17

news/2025/1/19 17:13:45/文章来源:https://www.cnblogs.com/Charlieljk/p/18337279

前言

比赛链接。

T1 没加记忆化莫名原因 T 飞了，T2 没做过 IO 交互不知道咋测样例干脆没交，T3 到现在还不知道为啥爆零了，赛时不知道咋合并背包根本不敢打，离线下来寻思快点结果全死了，T4 不可做题。

还是老毛病，遇到之前见的不多题型（尤其是 T1、T2 放）就寄，这次 T1 倒是没卡住（但是挂分了），加上 T2 直接死就唐了。

T1

原题：[ABC278F] Shiritori。

经典博弈论思路，若当前能够转移的状态全部为必胜，则此时为必败状态，否则为必胜状态，由此思路直接爆搜即可，若所有第一个选的节点中存在至少一个必胜状态则先手必胜。

直接搜复杂度是 \(n!\) 的，会寄掉，状压 + 记忆化使复杂度优化到 \(O(2^nn)\)。

点击查看代码

#include<bits/stdc++.h>
#define ll long long 
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=20,M=7e4+10;
template<typename Tp> inline void read(Tp&x)
{x=0;register bool z=true;register char c=getchar();for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);x=(z?x:~x+1);
}
template<typename Tp> inline void wt(Tp x)
{if(x>9)wt(x/10);putchar((x%10)+'0');}
template<typename Tp> inline void write(Tp x)
{if(x<0)putchar('-'),x=~x+1;wt(x);}
int n,f[N][M];
string s[N];
vector<int>e[N];
bool dfs(int x,int sta)
{if(x==0) {for(int i=1;i<=n;i++)if(!dfs(i,sta|(1<<(i-1))))return 1;return 0;}if(f[x][sta]!=-1) return f[x][sta];for(int y:e[x])if(!(sta&(1<<(y-1)))){if(!dfs(y,sta|(1<<(y-1))))return f[x][sta]=1;}return f[x][sta]=0;
}
signed main()
{read(n);for(int i=1;i<=n;i++) cin>>s[i];for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){if(i==j) continue;if(s[i][s[i].size()-1]==s[j][0])e[i].push_back(j);}memset(f,-1,sizeof(f));puts(dfs(0,0)?"First":"Second");
}

T2

原题：Nauuo and Binary Tree。

树链剖分。

首先询问 \(1\) 与 \(2\sim n\) 得到每个点的 \(dep\)，然后按照 \(dep\) 从小到大处理，这样在处理时比其深度小的一定已经处理过。

对于处理一点前先跑一遍 \(dfs\) 处理出其数剖状态，开始找 \(x\) 的父亲 \(y\)，先另 \(y=1\)，找到 \(y\) 这条重链上深度最大的节点 \(z\),通过询问 \(x,z\) 的距离可知 \(lca(x,z)\)，依据 \(dis(x,y)=dep_x+dep_y-2\times dep_{lca(x,y)}\)，且其 \(lca\) 一定在 \(y\) 这条重链上。找到其 \(lca\) 后有 \(x,z\) 在其不同子树上，因为其为一棵二叉树，所以 \(x\) 就在 \(y\) 的唯一那一条轻链上，另 \(y\) 等于 \(lca\) 的轻儿子，继续循环，直到 \(dep_x=dep_y+1\) 为止。

因为每次操作至少剖掉一半，所以每个点最多查询 \(\log n\) 次，故此总共最多查询 \(n+n\log n\) 次，看似擦边过不去但是跑不满。

点击查看代码

#include<bits/stdc++.h>
#define ll long long 
// #define endl '\n'
#define sort stable_sort
using namespace std;
const int N=3010;
template<typename Tp> inline void read(Tp&x)
{x=0;register bool z=true;register char c=getchar();for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);x=(z?x:~x+1);
}
template<typename Tp> inline void wt(Tp x)
{if(x>9)wt(x/10);putchar((x%10)+'0');}
template<typename Tp> inline void write(Tp x)
{if(x<0)putchar('-'),x=~x+1;wt(x);}
int n,dep[N],son[N][2],fa[N],bot[N],sz[N];
vector<int>e[N];
void dfs(int x)
{sz[x]=1,bot[x]=x;if(son[x][0]) {dfs(son[x][0]);sz[x]+=sz[son[x][0]];}if(son[x][1]){dfs(son[x][1]);sz[x]+=sz[son[x][1]];if(sz[son[x][0]]<sz[son[x][1]]) swap(son[x][0],son[x][1]);}if(son[x][0]) bot[x]=bot[son[x][0]];
}
void solve(int x)
{int y=1,dis;while(dep[y]!=dep[x]-1){printf("? %d %d",x,bot[y]);cout<<endl;read(dis);dis=(dep[x]+dep[bot[y]]-dis)/2;while(dep[y]<dis) y=son[y][0];if(dep[y]==dep[x]-1) break;y=son[y][1];}fa[x]=y;if(!son[y][0]) son[y][0]=x;else son[y][1]=x;
}
signed main()
{read(n);for(int i=2;i<=n;i++){printf("? 1 %d",i);cout<<endl;read(dep[i]);e[dep[i]].push_back(i);}for(int i=1;i<=n;i++){dfs(1);for(int x:e[i]) solve(x);}putchar('!');for(int i=2;i<=n;i++) putchar(' '),write(fa[i]);cout<<endl;
}

T3

原题：P6240 好吃的题目。

分治。

赛后感觉还挺好想的，但之前很少打过分治（好像压根没学但硬说也会），根本没想到，赛时想打莫队但不知道咋合并，还真有用莫队冲过去的，虽然这个复杂度不是很正确但数据水。

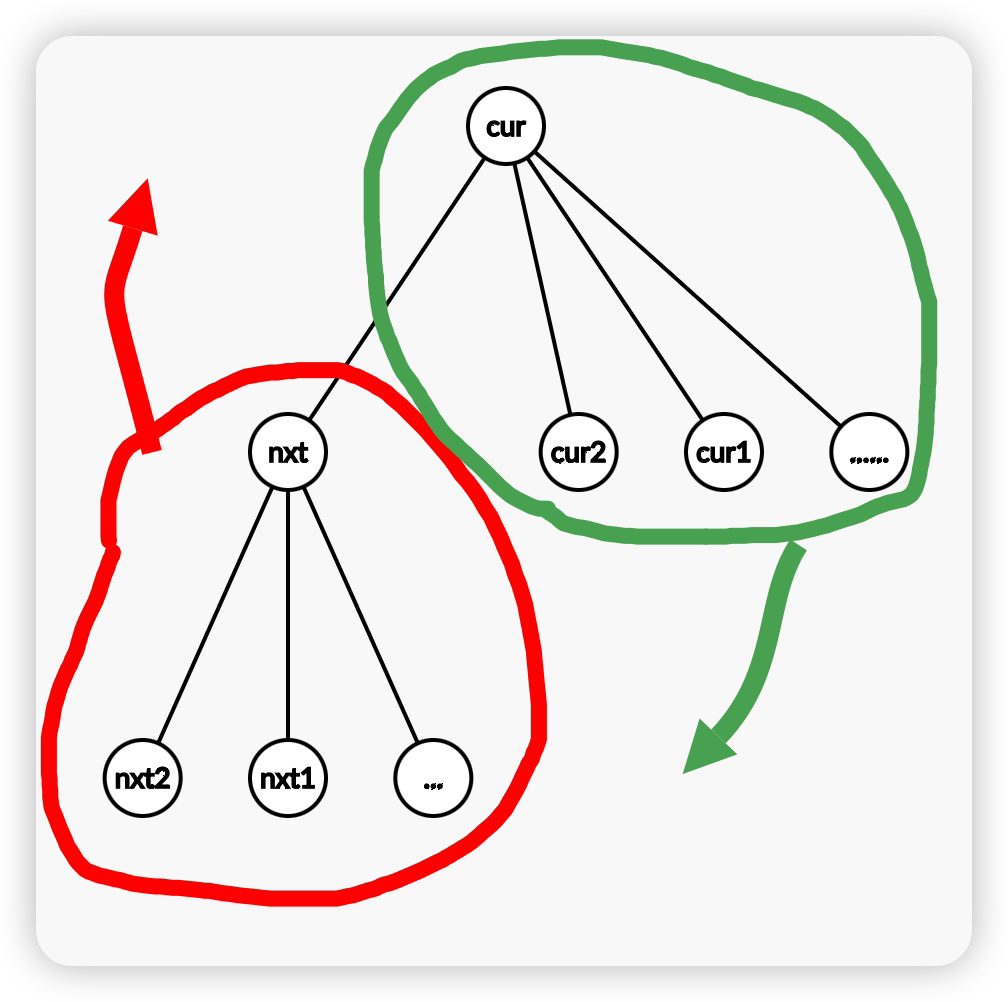
对于一个区间 \([l,r]\)，处理越过 \(mid\) 的询问，从 \(mid\) 开始分别向左向右跑，合并的时候有 \(ans_i=\max\limits_{j=0}^t\{f_{l_i,j}+f_{r_i,t_i-j}\}\) 即可。

点击查看代码

#include<bits/stdc++.h>
#define ll long long 
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=4e4+10,M=210,Q=2e5+10;
template<typename Tp> inline void read(Tp&x)
{x=0;register bool z=true;register char c=getchar();for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);x=(z?x:~x+1);
}
template<typename Tp> inline void wt(Tp x)
{if(x>9)wt(x/10);putchar((x%10)+'0');}
template<typename Tp> inline void write(Tp x)
{if(x<0)putchar('-'),x=~x+1;wt(x);}
int n,m,h[N],w[N],f[N][M],ans[Q];
struct aa {int l,t,id;};
vector<aa>pos[N];
void solve(int l,int r)
{if(l==r) {for(auto y:pos[r]){int x=y.l,t=y.t,id=y.id;if(x==l) ans[id]=t>=h[x]?w[x]:0;}return ;}int mid=(l+r)>>1;memset(f[mid],0,sizeof(f[mid]));memset(f[mid+1],0,sizeof(f[mid+1]));f[mid][h[mid]]=w[mid],f[mid+1][h[mid+1]]=w[mid+1];for(int i=mid-1;i>=l;i--){memcpy(f[i],f[i+1],sizeof(f[i]));for(int j=h[i];j<=200;j++)f[i][j]=max(f[i][j],f[i+1][j-h[i]]+w[i]);}for(int i=mid+2;i<=r;i++){memcpy(f[i],f[i-1],sizeof(f[i]));for(int j=h[i];j<=200;j++)f[i][j]=max(f[i][j],f[i-1][j-h[i]]+w[i]);}for(int i=l;i<=r;i++)for(int j=1;j<=200;j++)f[i][j]=max(f[i][j],f[i][j-1]);for(int i=mid+1;i<=r;i++)for(auto y:pos[i]){int j=y.l,t=y.t,id=y.id;if(j>=l&&j<=mid)for(int k=0;k<=t;k++)ans[id]=max(ans[id],f[i][k]+f[j][t-k]);}solve(l,mid),solve(mid+1,r);
}
signed main()
{read(n),read(m);for(int i=1;i<=n;i++) read(h[i]);for(int i=1;i<=n;i++) read(w[i]);for(int i=1,l,r,t;i<=m;i++){read(l),read(r),read(t);pos[r].push_back(aa{l,t,i});}solve(1,n);for(int i=1;i<=m;i++) write(ans[i]),puts("");
}

T4

原题：[AGC056B] Range Argmax。

不可做溜了溜了。

沾个官方题解

同一个 \(x\) 可能对应多个 \(p\)，因此这样计数比较困难。
考虑反过来计数。

对于给定的 \(x\)，我们将按照以下的方式构造 \(p\)：

令 \(p = (-1,-1,\cdots,-1)\) 。
我们从 \(n\) 开始依次递减地考虑每个值 \(v\)。对于每个值，我们找到 \(v\) 能放的最左侧的位置，放进去。

计数可以通过这种方式生成的 \(p\) 。

设当前最值为 \(v\)。我们首先确定下标 \(m\)，使得 \(p_m = v\)。对于所有包含 \(m\) 的区间 \(i\)，有 \(x_i = m\)。删除这些包含 \(m\) 的区间后，我们可以分别考虑位于 \(m\) 左右两侧的区间。由于 \(m\) 为最左侧的可以放 \(v\) 的位置，右侧的数均小于左侧的数，这部分是和原问题等价但规模更小的子问题。

现在考虑左侧。我们令 \(k\) 为 \(m\) 左侧最大元素对应的下标。有：必定存在一个左侧区间同时包含 \(k\) 和 \(m\)。
考虑反证。如果左侧没有区间同时包含 \(k\) 和 \(m\)，那我们可以令 \(p_k = v\)，这必定是更优且满足要求的。这与假设矛盾，因此必定存在同时包含 \(k\) 和 \(m\) 的左侧区间。
因此，左侧区间所填的数的最大值必定大于等于 \(v\)。