匈牙利算法--二分图的最大匹配
给定一个二分图,其中左半部包含 n1个点(编号 1∼n1),右半部包含 n2 个点(编号 1∼n2),二分图共包含 m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
二分图的匹配:给定一个二分图 G,在 G的一个子图 M 中,M的边集 {E}中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
输入格式
第一行包含三个整数 n1、 n2和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示左半部点集中的点 u 和右半部点集中的点 v之间存在一条边。
输出格式
输出一个整数,表示二分图的最大匹配数。
数据范围
1≤n1,n2≤500
1≤u≤n1
1≤v≤n2
1≤m≤105
输入样例:
2 2 4
1 1
1 2
2 1
2 2输出样例:
2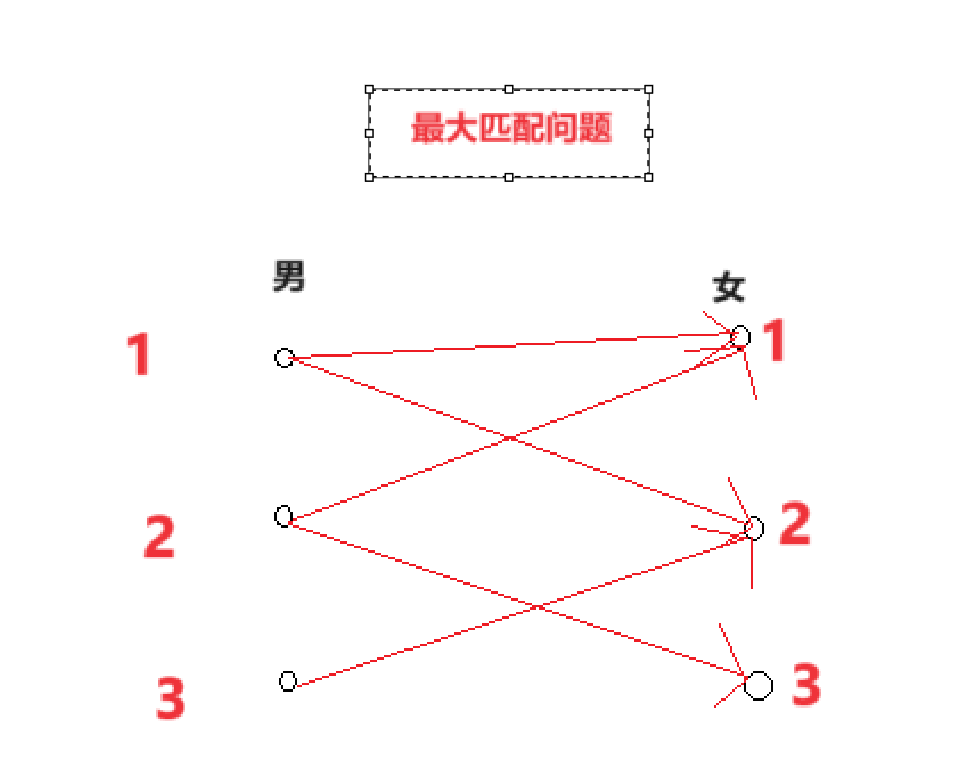
最大匹配问题分析:
从左到右每个男生搭配不同的女生
做法是利用邻接表存放从左到右的图
然后遍历所有男生看每个男生选不同的女生最多有几个男生能实现-->对于每个男生遍历他相连接的女生,前提是女生没被遍历,且女生没有被别的男生选或者选这个女生的男生不选这个女生还有备选女生。find函数
match数组:match[i]=a表示第i个女生搭配第a个男生
男女用数字1~表示
#include<bits/stdc++.h>
//单向,从左到右
using namespace std;
int n1,n2,m;
const int N=600;//一边的
const int M=100008;//边数
bool st[N];//这个顶点有没有访问过,右边的顶点
//邻接表
int h[N];//头指针
int e[M];//当前
int ne[M];//下一个
int match[N];//女搭配哪个男
int idx;
void add(int a,int b){//邻接表
e[idx]=b;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
bool find(int a){
for(int i=h[a];i!=-1;i=ne[i]){
int t=e[i];
if(!st[t]){//这个相邻点没遍历过
st[t]=true;//遍历
if(match[t]==0||find(match[t])){
match[t]=a;
return true;
}
}
}
return false;
}
int main(){
cin>>n1>>n2>>m;
memset(h,-1,sizeof h);
int a,b;
while(m--){//邻接表
cin>>a>>b;
add(a,b);
}
int res=0;
for(int i=1;i<=n1;i++){
memset(st,false,sizeof st);
if(find(i)){
res++;
}
}
cout<<res;
return 0;
}