设红色的点值为 0,蓝色为 1。
注意到,如果有一条边的颜色和两端点同色,一定可以选。
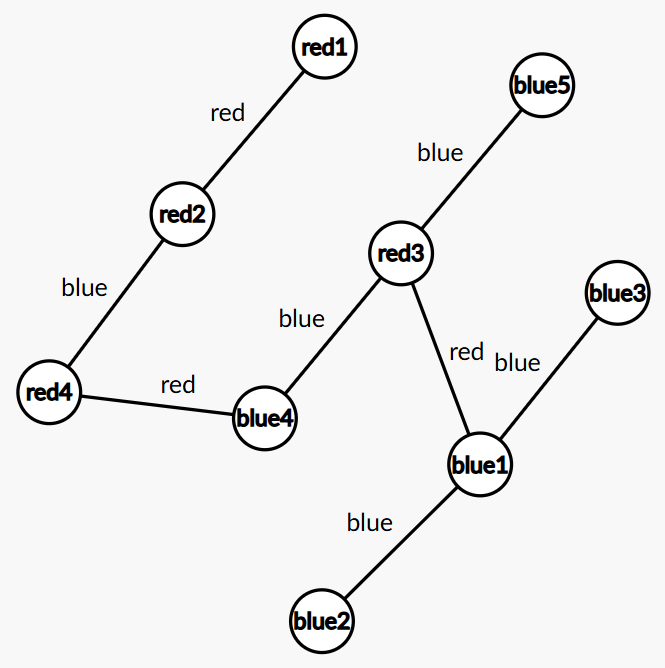
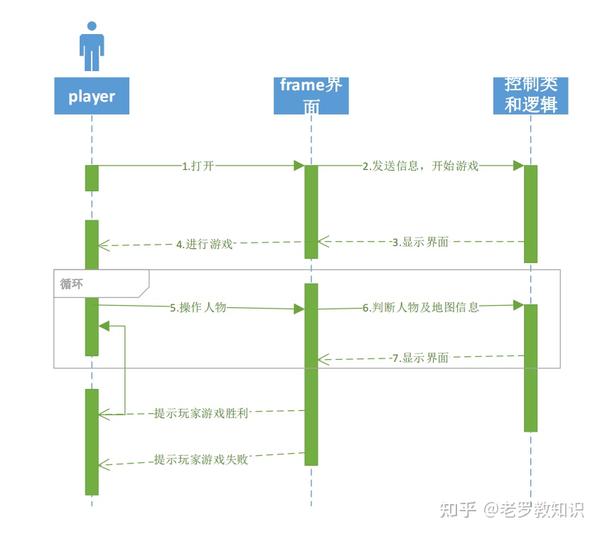
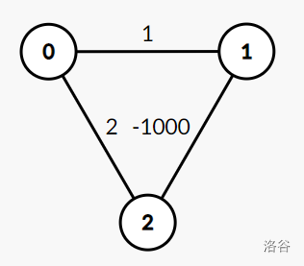
例子:

选择和两端点同色的边。
又发现,如果存在一个 \(sz>1\) 的合法连通块,无论和其他点怎么连,原来的这个连通块内的点一定合法。
有注意到形如 \(0\xleftrightarrow 10,1\xleftrightarrow 01\) 类型的边,除了连接两个 \(sz>1\) 的块外,无用。
那么 \(0\xleftrightarrow x1\) 这样的呢?
注意到,只用上面这种边不可能形成一个连通块,因为每次加入这种边的时候,一定只会满足一边,没有被满足的点只会移动而不会消失。
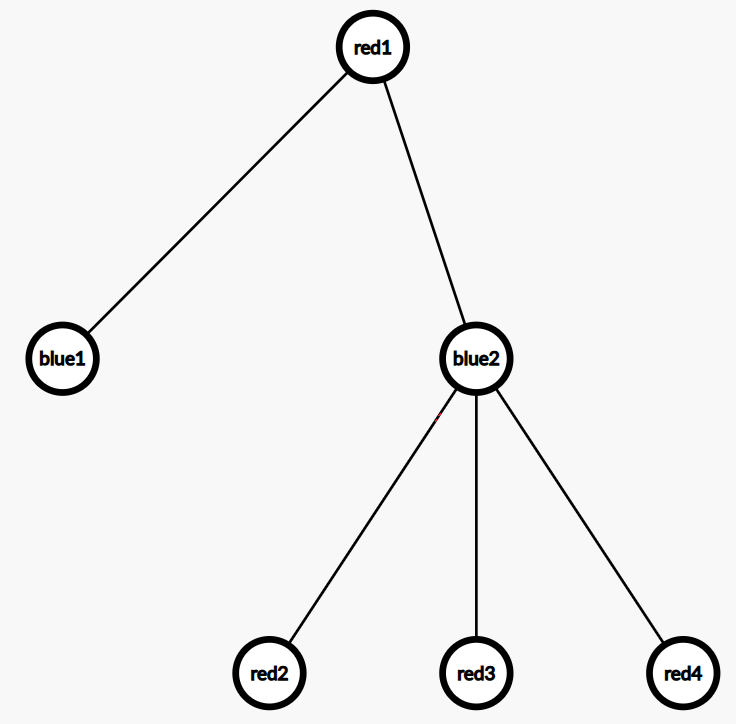
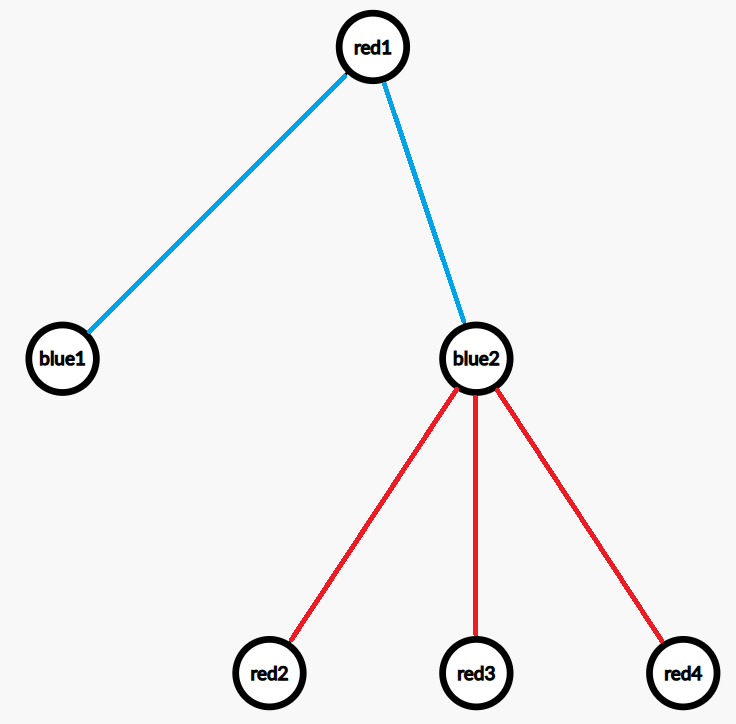
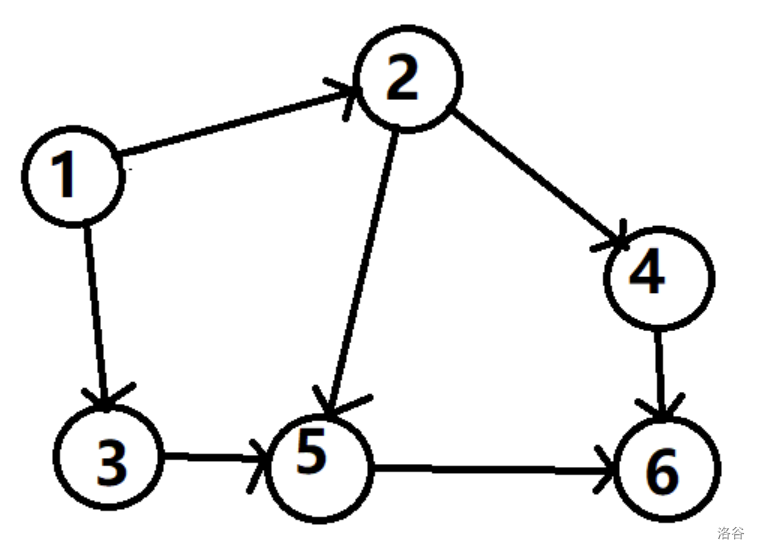
如图,即使贪心染色,根节点也无法满足。
所以,一定是从一开始的一些大连通块开始,沿着 \(0\xleftrightarrow 11\) 这样的边搜索。
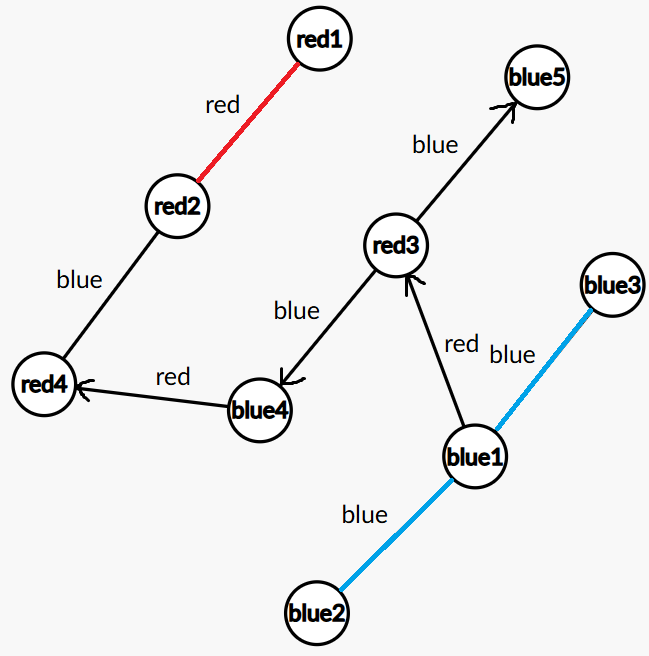
搜索有点细节,因为加入孤立点要先满足孤立点的需求,所以 \(0\xleftrightarrow x1\) 的边的搜索方向应该是 \(!x\to x\)。
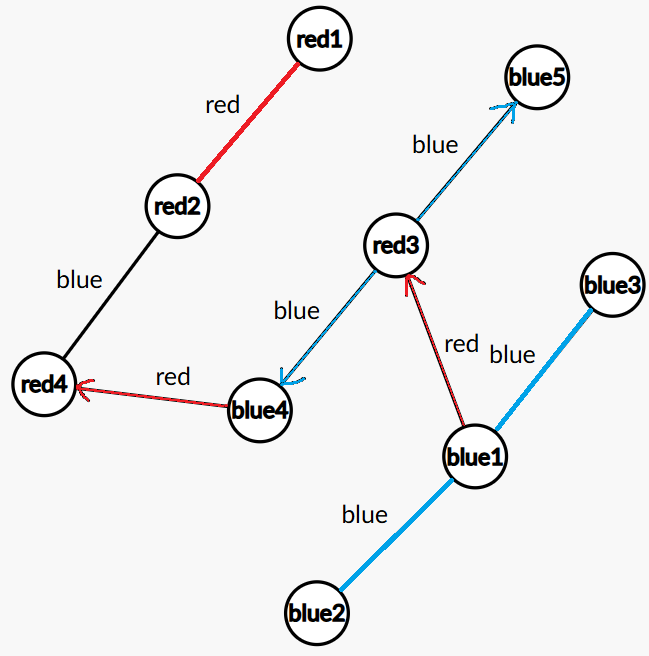
最后合并成几个大连通块。
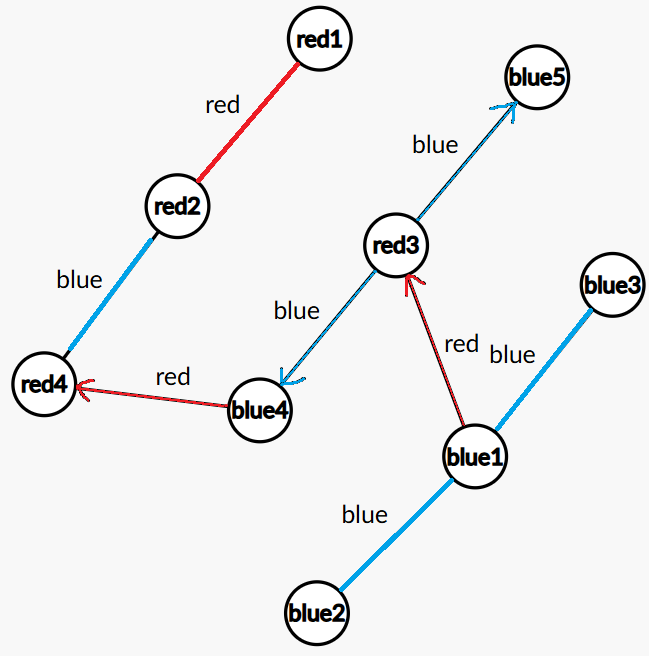
然后用 \(0\xleftrightarrow 10,1\xleftrightarrow 01\) 类型的边合并,就做完了。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;const int N = 2e5 + 5;
int fa[N], n, m;int find(int x) {return x == fa[x] ? x : fa[x] = find(fa[x]);}
inline bool conn(int x, int y) {return find(x) == find(y);}
void merge(int x, int y) {fa[find(x)] = find(y);}int u[N], v[N], w[N], c[N];
bool ok[N], ch[N];vector<pair<int, int>> e[N];signed main()
{ios::sync_with_stdio(0);cin.tie(0);cin >> n >> m;for(int i = 1; i <= n; i ++) fa[i] = i;for(int i = 1; i <= m; i ++){char c; cin >> u[i] >> v[i] >> c;w[i] = c == 'R';}string s; cin >> s;for(int i = 1; i <= n; i ++)c[i] = s[i - 1] == 'R';for(int i = 1; i <= m; i ++){int x = u[i], y = v[i], z = w[i];if(conn(x, y)) continue;if(z == c[x] && z == c[y])merge(x, y), ok[x] = ok[y] = 1, ch[i] = 1;else if(z == c[x]) e[y].push_back({x, i});else if(z == c[y]) e[x].push_back({y, i});}queue<int> q;for(int i = 1; i <= n; i ++) if(ok[i]) q.push(i);while(q.size()){int t = q.front(); q.pop();for(auto [i, id] : e[t])if(!conn(t, i)){ch[id] = 1;merge(t, i);if(!ok[i]) q.push(i);ok[i] = 1;}}for(int i = 1; i <= n; i ++)if(!ok[i]) return cout << "No", 0;for(int i = 1; i <= m; i ++)if(!conn(u[i], v[i])) merge(u[i], v[i]), ch[i] = 1;cout << "Yes\n";for(int i = 1; i <= m; i ++)if(ch[i]) cout << i << " ";return 0;
}