Contest
A 签到题
B 最大流
Dinic 板子。
Dinic 的整体结构:
ll dinic() {ll ans = 0;while (bfs()) { // 如果 s 还有能到 t 的增广路fill(cur+1, cur+n+1, 0); // 当前弧优化的预处理,暂时不用管ans += dfs(s, INF); // 多路增广}return ans;
}
BFS 建分层图:
bool bfs() {fill(level+1, level+n+1, 0); // 清空上一次的分层queue<int> q;level[s] = 1, q.push(s);while (!q.empty()) {int u = q.front(); q.pop();for (auto [v, i] : G[u]) {if (!level[v] /*没 BFS 到过*/ && c[i] > f[i] /*还有残量*/) {level[v] = level[u] + 1; // 把 v 扔到 u 的下一层q.push(v);}}}return level[t] != 0; // 能从 s 到 t
}
DFS 多路增广:
ll dfs(int u, ll flow) {if (u == t)return flow;ll tmp = flow; // 当前还有多少流能用for (int &idx = cur[u]; idx < int(G[u].size()); idx++) { // 当前弧优化,之前走过的不要再走auto [v, i] = G[u][idx];if (level[v] != level[u] + 1) // 在分层图上不是下一层就别去continue;ll t = dfs(v, min(tmp, c[i] - f[i])); // min(能用的流, 这条边的残量)f[i] += t;f[i ^ 1] -= t;tmp -= t;if (tmp == 0) // 没流了break;}return flow - tmp; // 总共用了多少流
}
完整代码:
#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = (l); i <= (r); i++)
#define per(i, r, l) for (int i = (r); i >= (l); i--)
using namespace std;
typedef long long ll;const int MAXN = 200 + 5;
const int MAXM = 5e3 + 5;
const ll INF = 1e12;int n, m, s, t;
vector<pair<int, int>> G[MAXN];
ll c[MAXM * 2], f[MAXM * 2];
int level[MAXN], cur[MAXN];bool bfs() {fill(level+1, level+n+1, 0);queue<int> q;level[s] = 1, q.push(s);while (!q.empty()) {int u = q.front(); q.pop();for (auto [v, i] : G[u]) {if (!level[v] && c[i] > f[i]) {level[v] = level[u] + 1;q.push(v);}}}return level[t] != 0;
}
ll dfs(int u, ll flow) {if (u == t)return flow;ll tmp = flow;for (int &idx = cur[u]; idx < int(G[u].size()); idx++) {auto [v, i] = G[u][idx];if (level[v] != level[u] + 1)continue;ll t = dfs(v, min(tmp, c[i] - f[i]));f[i] += t;f[i ^ 1] -= t;tmp -= t;if (tmp == 0)break;}return flow - tmp;
}
ll dinic() {ll ans = 0;while (bfs()) {fill(cur+1, cur+n+1, 0);ans += dfs(s, INF);}return ans;
}int main() { ios::sync_with_stdio(0); cin.tie(0);cin >> n >> m >> s >> t;rep(i, 1, m) {int u, v, w; cin >> u >> v >> w;G[u].emplace_back(v, i << 1), c[i << 1] = w;G[v].emplace_back(u, i << 1 | 1);}cout << dinic() << '\n';return 0;
}
C 防鼠工程
洛谷原题 P4001 [ICPC-Beijing 2006] 狼抓兔子。
简要题意:给定一张如下的 \(n \times m\) 的网格图,求其最小割。\(n,m \le 10^3\),保证输入文件的大小在 10M 以内。
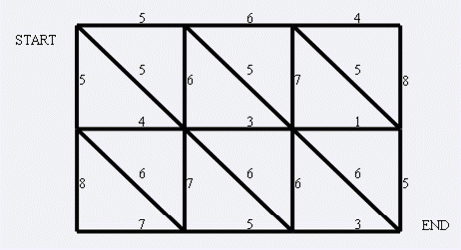
Sol 1: 最小割 = 最大流
根据最大流最小割定理,最小割等于最大流,Dinic 硬跑最大流即可。
时间复杂度为玄学,虽然点边都到 \(10^6\) 级别,但是可能是因为图的特殊性质它 2s 跑过去了。
开 long long 会被卡空间,开 int 能过。
Sol 2: 平面图最小割 = 对偶图最短路
考虑把整张图割开就是要从左下角的空白区域找一条路一直割到右上角的空白区域,我们建出对偶图跑最短路 Dijkstra 即可。说不定 SPFA 也能过,毕竟特殊图
这次时间复杂度不是玄学,是 \(O(n^2 \log n)\)。
D 坐座位
简要题意:给定一张稠密的二分图,求其最大匹配。设左部点数量为 \(n_1\),右部点数量为 \(n_2\),\(n_1,n_2 \le 200\)。
匈牙利算法板子
建模:令 \(s = n_1 + n_2 + 1, t = n_1 + n_2 + 2\)。原图的每条边 \(u \rightarrow v\) 边权设为 \(1\),给所有左部点 \(u\) 连边 \(s \rightarrow u\) 边权为 \(1\),给所有右部点 \(v\) 连边 \(v \rightarrow t\),跑 Dinic 即可。
值得注意的是,Dinic 跑二分图的时间复杂度为 \(O(\sqrt n m)\),不是玄学。
坑点:
- 右部点的编号要加上 \(n_1\)
MAXN要开到 \(n_1 + n_2\),也就是两倍 \(n_1\)MAXM要开到 \(m + n_1 + n_2\)(不算反向边)- \(n\) 要开到 \(n_1 + n_2 + 2\),也就是 \(t\)