任务
77. 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
思路
组合思路
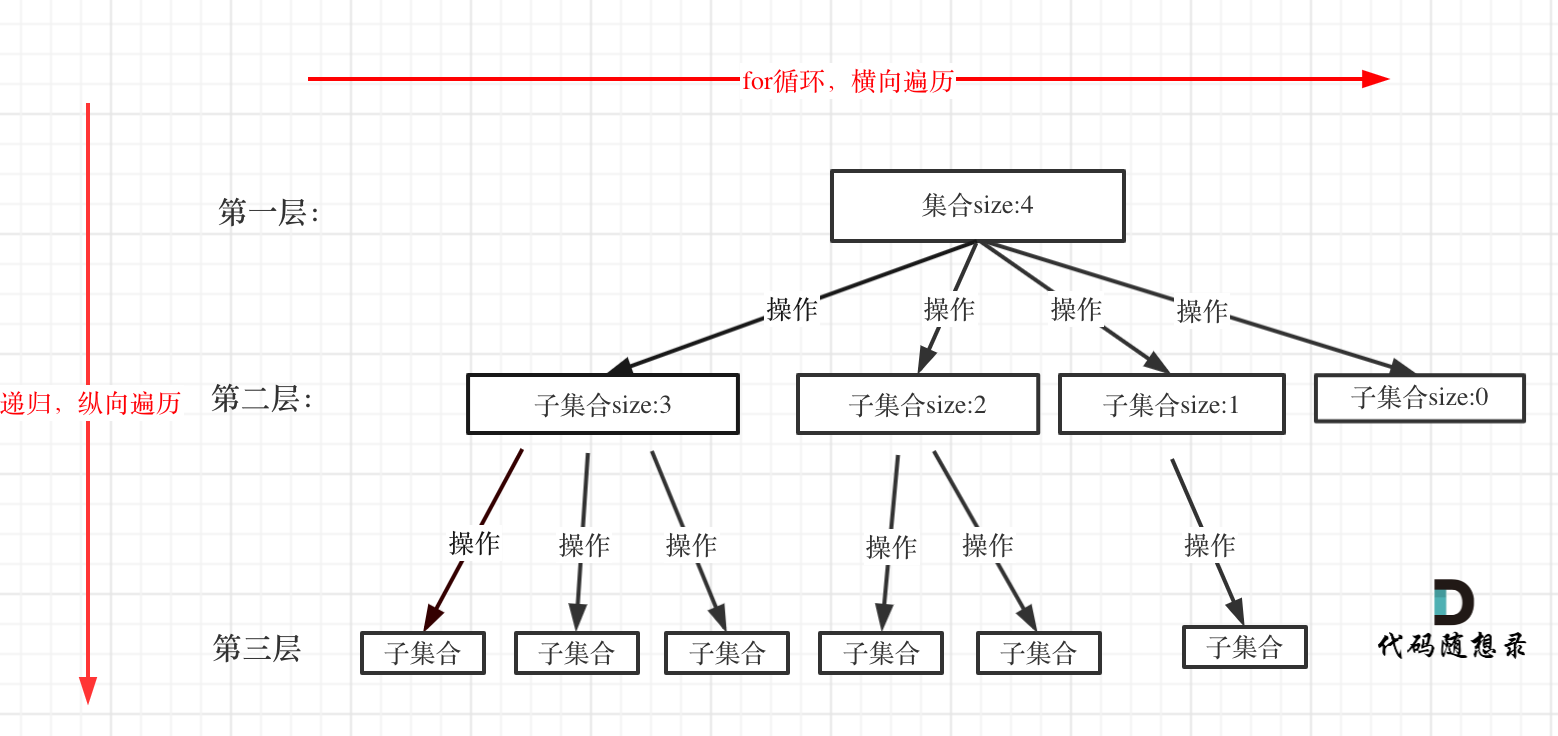
对于组合问题,是在一个集合中取不同的数,构成各种组合,本质上是一个多叉树的路径问题,即递归序遍历多叉树并收集信息,并且带一些条件,比如本题是收集K个元素,即收集所有K个节点的路径。把根节点当作虚拟头节点(假设为第一层),每次取一个数,横向看,每个节点就是每次选择的数的所有可能,纵向看,某条路径最终收集到K个就是其中的一个结果。
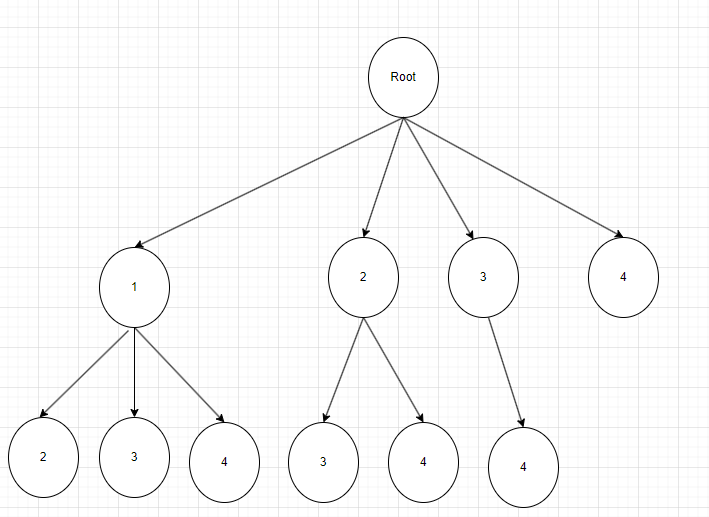
如图所示就是一个从4个数中找所有两个数的多叉树示意图(3层,未画出的部分不可能向下寻找了,已经找够了),终止条件就是路径的长度达到要求K个。想要用回溯或者说递归去收集节点的值,需要思考,什么驱动了递归的进行,这道题中,是通过start,即每次递归的开始索引来驱动的。如,第一次选1,在第二次选取中,就得从2开始选。同理,第一次选2,第二次选取的时候,就得从3开始选。逻辑就是利用递归序遍历这颗多叉树,每次到达最底层后,收集到结果中即可。注意返回上层时的回溯。
剪枝
此外,可以剪枝的操作来让程序不用遍历整棵树,比如还是以上图中n=4,k=2举例,那么第一层最后4这个节点就可以不遍历,因为需要组成路径的节点已经不够了。如果是k=3,那么这里第一层的3,4两棵子树都不需要遍历了,同样因为需要组成路径的剩余节点已经不够了。具体和推导过程如下:需要保证[x,n+1)的数组长度起码要满足
n+1-x = k-len(self.path) => x 至多 == n+1-(k-len(self.path)) ,又由于开区间,为了取到这个值,再加1,具体看代码
为啥不能用循环
因为循环的层数是不定的,k个数的组合,就需要k层循环。因此想到用递归的深度控制这个k,路径长度达到k后,或者说树向下遍历到k层后,就可以记录其中一条结果,按照递归序依次遍历,将所有k层的路径全部记录,就完成了题意所需的k个数的组合。
class Solution:def __init__ (self):self.path = []self.paths = []def combine(self, n: int, k: int) -> List[List[int]]:self.dfs(n,k,1)return self.pathsdef dfs(self,n,k,start):if len(self.path) == k: # 已经收集了k个数,到了统计结果的时候self.paths.append(self.path[:])return# for i in range(start,n+1): #递归序收集节点值for i in range(start,n+2-(k-len(self.path))): # [x,n+1)的数组长度起码要满足 n+1-x = k-len(self.path) => x 至多 == n+1-(k-len(self.path)) ,又由于开区间,为了取到这个值,再加1self.path.append(i)self.dfs(n,k,i+1)self.path.pop()
216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
思路
这道题与上一题中的组合相比,就添加了一个条件,即和为n,那么我们在写终止条件的时候,只要加上这个条件,以及在递归中,修改和的值即可。
另外可以剪枝,横向上就是减少循环的次数,纵向上,如果已经和大于n(因为节点值全是正数,向下找不可能在累加和为n的节点),则直接返回。
class Solution:def __init__(self):self.path = []self.paths = []self.sum = 0def combinationSum3(self, k: int, n: int) -> List[List[int]]:self.dfs(n,k,1)return self.pathsdef dfs(self,n,k,start):if self.sum > n: # 竖向剪枝return if len(self.path) == k: if self.sum == n:self.paths.append(self.path[:])return#for i in range(start,10):for i in range(start,11-(k-len(self.path))): #[x,10)的长度至少满足 10-x = k-len(self.path) ,x 至多== 10-k-len(self.path) ,开区间的情况下,再加1 (横向剪枝)self.path.append(i)self.sum += iself.dfs(n,k,i+1)self.sum -= iself.path.pop()
17. 电话号码的字母组合
思路
首先,循环是不行的,因为你不知道由多少个数字(有一个循环1次,有n个循环n次,即循环次数补丁)
思考递归,如何构建这个问题的多叉树,递归深度来控制数字个数,考虑用index(表示当前处理到的digits的元素的索引)来驱动递归函数。
比如"23",则第一次在abc中选一个,第二次在def中选一个。注意,纵向的递归序遍历驱动是由index的增加驱动的,表示处理digits中的每个元素,横向的是由每次的for循环驱动的,表示遍历每个字符串(如'abc','def')
class Solution:def __init__(self) -> None:self.path = ""self.paths = []self.digitMap = {2:'abc',3:'def',4:'ghi',5:'jkl',6:'mno',7:'pqrs',8:'tuv',9:'wxyz'}def letterCombinations(self, digits: str) -> List[str]:if not digits:return []self.dfs(digits,0)return self.pathsdef dfs(self,digits,index):if len(self.path) == len(digits):self.paths.append(self.path[:])returndigit = int(digits[index])str = self.digitMap[digit] #digit代表的字符组成的字符串for c in str:self.path += cself.dfs(digits,index+1)self.path = self.path[:-1]
心得体会
个人在回溯问题相关的内容中的思路与代码随想录有略微不同,我是将值放在节点上(随想录是放在边上),然后按照多叉树的递归序遍历的逻辑去思考。这个思路是收到二叉树章节左右子树的递归序遍历的启发,感觉相对更好理解。
注意for循环的最外层(最上层的递归函数)就是树的第二层,逻辑上它是由第二层开始的,或者说是由循环开始的,然后每个节点进行递归调用往下深入,这与二叉树的从根开始由一点细微的区别,注意体会。
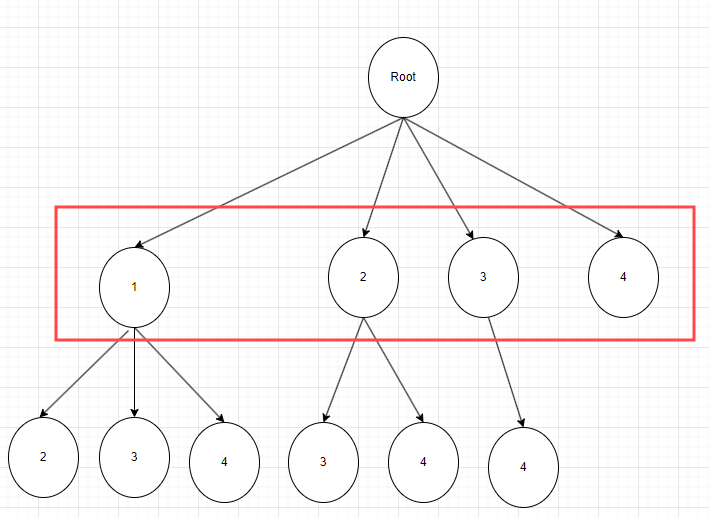
其次在本节中学习了剪枝的技术,以避免暴力递归造成的较高的时间成本。剪枝分为横向剪枝和纵向剪枝。
横向一般就是修改循环的size,避免遍历不可能成为结果的子树(比如组合中剩余节点数量不满足的那些),而纵向剪枝是根据条件,如果当前树继续遍历下去是不可能得到结果的,则直接返回。(比如组合总和中,遍历并累加到某节点的和已经大于sum,继续向下遍历没有意义,则直接剪枝返回)