雷达气象学（8）——反射率因子图分析（非气象回波篇）

目录

• 8.0 雷达回波的分类
• 8.1 地物回波
• 8.2 海浪回波
• 8.3 干扰回波（同波长干扰）
• 8.4 生物回波
• 8.5 超折射回波
• 8.6 旁瓣回波

8.0 雷达回波的分类

雷达回波可分为气象回波和非气象回波：

\[雷达回波 \begin{cases}气象回波 \begin{cases}层状云降水回波 \\积状云降水回波（对流性降水回波） \\层积混合降水回波 \\零度层亮带 \\晴空回波 \\\end{cases} \\非气象回波 \begin{cases}地物回波 \\海浪回波 \\干扰回波 \\生物回波 \\超折射回波 \\旁瓣回波 \\\end{cases} \end{cases} \]

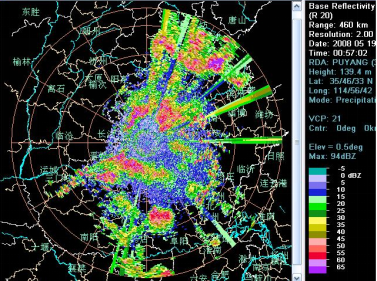
8.1 地物回波

地物杂波有两种，一种是固定地物回波，另一种是超折射地物回波，这一节所说的是第一种，第二种在“超折射回波”那节会讲到。

（1）产生原因：山丘、岛屿、高大建筑等地物对电磁波的反射作用。

（2）回波特征：强度很强，一般大于 45dBZ；主要影响最低仰角产品；发生在距离雷达较近的地方。

（3）判别方法：

• 地物回波边缘清晰，呈无规则排列；
• PPI 图上，地物高度比较低，抬高雷达仰角发现地物杂波逐渐消失；
• 地物基本是固定的，因此地物回波的径向速度接近于零；
• 地物回波不随时间发生移动和变化，可翻看前后时次的反射率因子图对比查看。

8.2 海浪回波

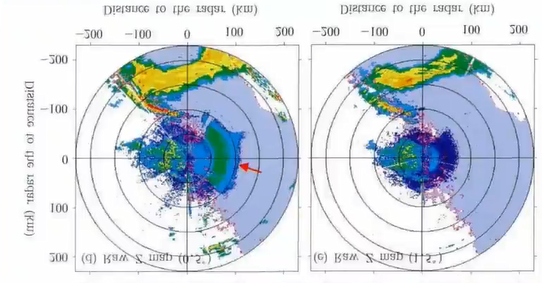
（1）产生原因：一般在沿海测站发生，由超折射引起。

（2）回波特征：由许多针状组成，呈扇形向外辐射，强度弱且均匀。

8.3 干扰回波（同波长干扰）

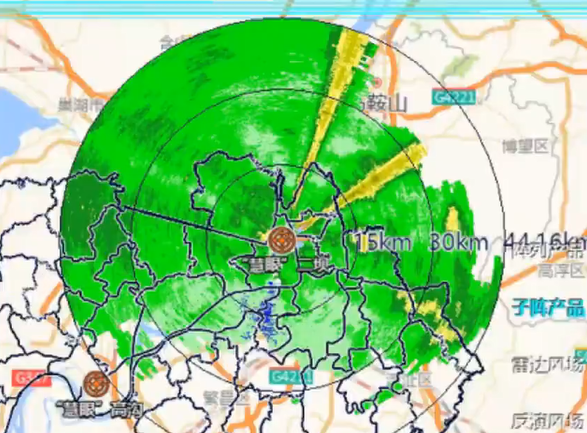
（1）产生原因：近距离有两部以上波长相同的雷达同时工作，一部雷达发射出来的电磁波能量通过地物或降水的散射，进入另一部雷达接收机。

（2）回波特征：单条或多条线状，点线状回波带，从中心以等间隔呈螺旋状向四周辐射。

8.4 生物回波

鸟、昆虫及其他飞行生物所产生的回波称为生物回波。在以前，生物回波被视为“杂波”，如今则经常被用于监测空中迁飞生物，应用于农业、林业、草原病虫害预报和防治等领域。欧美等国也有利用天气雷达来追踪空中迁飞生物的研究和实践。其中，对鸟类的探测及相关算法相对成熟。

生物回波的主要特征有：

• 若飞行生物是成群出现的，则回波为片状或线状；若是孤立出现的，则回波为点状；
• 昆虫回波的反射率比鸟类回波稍弱，一般小于 35dBZ；
• 飞行生物的高度有限，回波一般出现在低仰角，距离雷达较近；
• 生物具有昼伏夜出或昼出夜伏的特征，回波也随之变化。

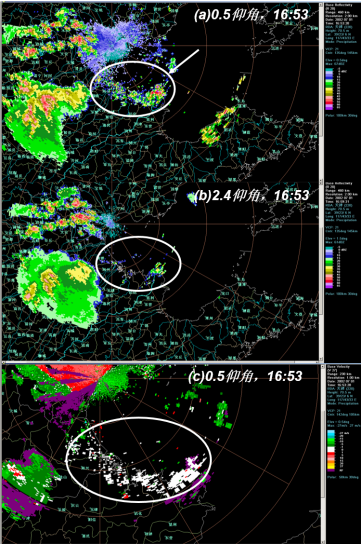
8.5 超折射回波

与地物杂波相似，超折射地物回波也是来自于地物。

（1）产生原因：大气中折射指数随高度迅速减小造成，往往出现在逆温或湿度随高度迅速减小的情况下。

（2）回波特征：

• 雷达回波显示中，地物回波显著增多、增强；
• 在 PPI 上，超折射回波常常是一些呈幅轴状排列的短线。
• 在 RHI 上，超折射回波与地物回波相似，呈短而窄的柱状，两头尖，高度低；
• 在大气层中，形成超折射的气层通常只是近地面很薄的气层（100~1000m），所以可适当提高仰角，雷达波能穿透超折射层，可使得超折射回波大大减少；
• 在径向速度图上，一个接近零的速度场中可能会孤立地镶嵌着非零值，这些非零值可能由海浪、汽车、飞机、船只、鸟等引起。

8.6 旁瓣回波

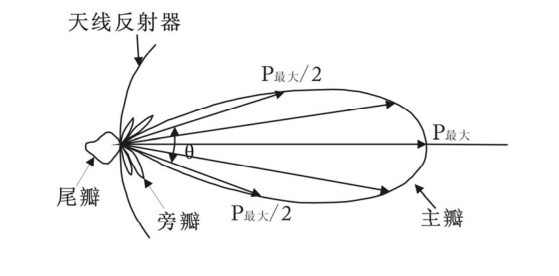
先复习一下天线方向图，如上图所示，最大辐射能量的发射方向称为主瓣，侧面称为旁瓣。

在通常情况下，旁瓣所产生的能量很弱；但是当旁瓣碰到强反射率目标物（如雷暴内的强降水柱或冰雹）时，能返回足够被识别的能量，从而产生旁瓣回波。如下图所示，雷达在旋转扫描过程中，主瓣还没扫到强回波区时，旁瓣已经碰到强回波区并散射回雷达，但雷达又将其定位到主瓣所在的径向上，从而出现这种虚假的回波。

旁瓣回波的特征有：

• 在 RHI 上，正好在云内强回波区的正上方出现一条细长的强度较弱的回波，向上延伸。由于旁瓣的天线增益比主瓣低得多，所以旁瓣回波的强度较弱，一般只有在雷暴距离雷达较近时才可能观测到。
• 在 PPI 上，位于雷达回波梯度大且强的一侧，其出现的高度与云内强回波区的高度一致。

关于旁瓣回波，在后面介绍强雷暴或强对流天气时可能也会再提到一次。