- 前言
- 一、非线性规划的标准型
- 二、fmincon函数
- 1.目标函数--function f = fun(x)
- 2.非线性约束函数--[c,ceq] = nonlfun(x)
- 3.设置求解方法--option
- 三、matlab求解非线性规划的实例与可能遇到的问题
- 1.初值问题
- 2.算法问题
- (1)内点法求解
- (2)SQP算法求解
- (3)active set算法求解
- (4)信赖域反射算法求解
前言
描述目标函数或约束条件的数学表达式中,至少一个是非线性函数,这样的优化问题通常称为非线性规划。一般说来,解决非线性规问题要比解决线性规划问题困难得多。线性规划有适用于一般情况的单纯形法,但是于非线性规划问题,目前还没有一种适用于一般情况的求解方法,现有各种方法都有各特定的适用范围。本章会介绍如何用matlab内置的不同算法解决非线性规划问题。
一、非线性规划的标准型
非线性规划的标准型相比线性规划多了一个非线性不等式约束与非线性等式约束,其与线性约束的区别在于非线性约束需要把等号的右边全部化成0
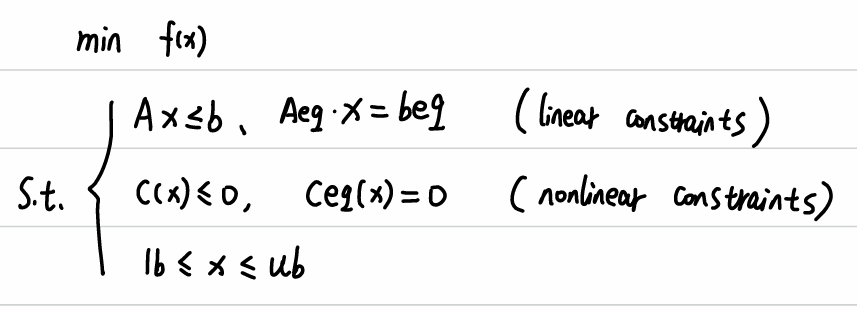
二、fmincon函数
[x,fval] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)
x0表示给定的初始值(用行向量或者列向量表示),必须得写,而且对求解十分重要
@fun表示目标函数,不再像线性规划的函数仅用系数向量这么简单来表示,需要在同一文件目录下创建一个函数文件
@nonlfun表示非线性约束的函数
option 表示求解非线性规划使用的方法
1.目标函数--function f = fun(x)
此参数是一个保存在同一文件夹下的函数文件,其中x是一个向量,写的时候不能直接写x1,x2;而是要用x(1),x(2)来表示向量中的元素
function f = fun(x)
% max f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2f = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ;
end
2.非线性约束函数--[c,ceq] = nonlfun(x)
这里的c是一个非线性不等式约束,ceq是非线性等式约束,他们的写法也是把x当作一个向量,用x(1)来引用x里面的元素。
同时,需要把约束的右侧全部化为0,填入约束的左侧
function [c,ceq] = nonlfun2(x)% 非线性不等式约束c = [-x(1)^2+x(2)-x(3)^2; % 一定要注意写法的规范,再次强调这里的x是一个向量!不能把x(1)写成x1x(1)+x(2)^2+x(3)^2-20];% 非线性等式约束ceq = [-x(1)-x(2)^2+2;x(2)+2*x(3)^2-3];
end
3.设置求解方法--option
matlab为求解非线性约束提供了几种方法,可以通过命令来调用,在比赛中,我们可以在论文中说明我们使用了不同方法,并描述哪一种方法更好
(1)内点法-- matlab默认的求解方法
option = optimoptions('fmincon','Algorithm','interior-point')
(2)序列二次规划法
option = optimoptions('fmincon','Algorithm','sqp')
(3)有效集法
option = optimoptions('fmincon','Algorithm','active-set')
(4)信赖域反射算法(对约束有要求)
option = optimoptions('fmincon','Algorithm','trust-region-reflective')
三、matlab求解非线性规划的实例与可能遇到的问题
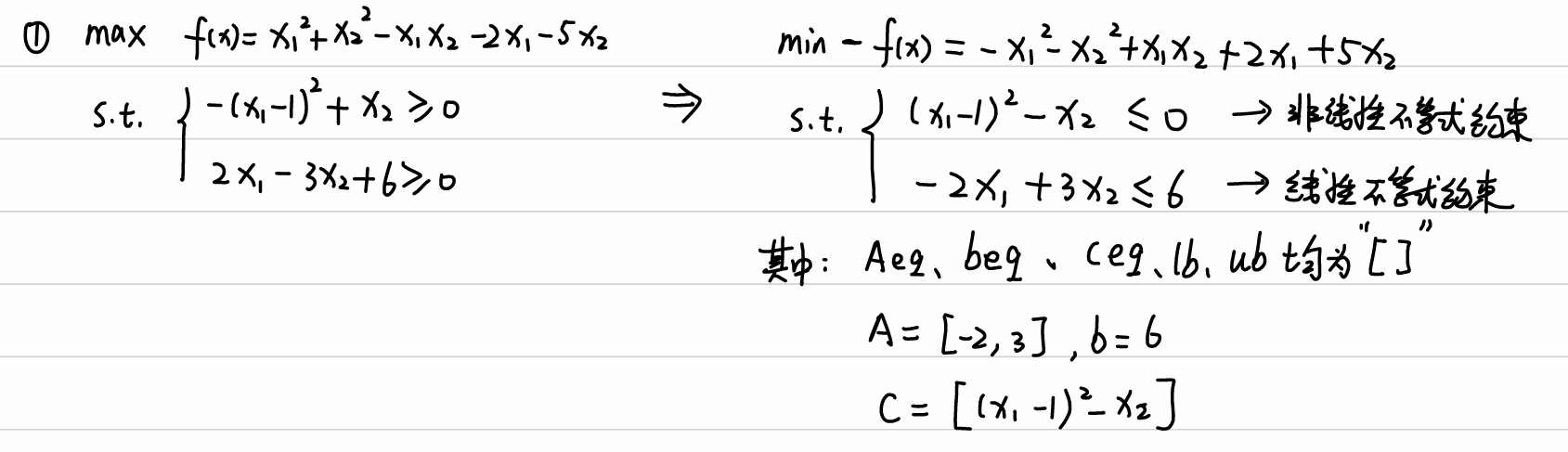
1.初值问题
x0 = [0 0]; x1 = [40.8, 10.8] %任意给定一个初始值
A = [-2 3]; b = 6;
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1) % 注意 fun1.m文件和nonlfun1.m文件都必须在当前文件夹目录下
fval = -fval
当选定x0作为初值时,结果:x=[1.00000001604465,6.66655111798166e-08]
fval=-1.00000039999306
当选定x1作为初值时,结果:x=[1.5123164061584e+22,-1.85553223470542e+52]
fval=3.4429998740309e+104
这说明初值对求解的影响很大,不同的初值给出的结果天差地别,而且让x1作为初值时,得到的结果应该也不满足我们的约束。(或许我们的初值就不满足约束)
因此,找到一个合适的初值对解决我们的问题时非常重要的
使用蒙特卡罗的方法来找初始值(推荐),在蒙特卡罗的方法的循环过程中,不必再加入判断等式约束的条件,因为我们可以通过等式约束的条件来生成随机数
2.算法问题
(1)内点法求解
option = optimoptions('fmincon','Algorithm','interior-point')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval
x =[1.00000001604465,6.66655111798166e-08]
fval =-1.00000039999306
(2)SQP算法求解
option = optimoptions('fmincon','Algorithm','sqp')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval %得到-4.358,远远大于内点法得到的-1,猜想是初始值的影响
% 改变初始值试试
x0 = [1 1]; %任意给定一个初始值
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option) % 最小值为-1,和内点法相同(这说明内点法的适应性要好)
fval = -fval
(3)active set算法求解
option = optimoptions('fmincon','Algorithm','active-set')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval
结果:
x =[-0.333333399760948,1.7777777334927]
fval =-4.35802434691854
(4)信赖域反射算法求解
option = optimoptions('fmincon','Algorithm','trust-region-reflective')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval

这说明这个算法不适用我们这个约束条件,所以以后遇到了不能求解的情况,记得更换其他算法试试!!!