多元/多维高斯/正态分布概率密度函数推导 (Derivation of the Multivariate/Multidimensional Normal/Gaussian Density)

news/2024/9/21 10:46:35/文章来源:https://www.cnblogs.com/Gaowaly/p/18354054

各种维度正态分布公式：

一维正态分布

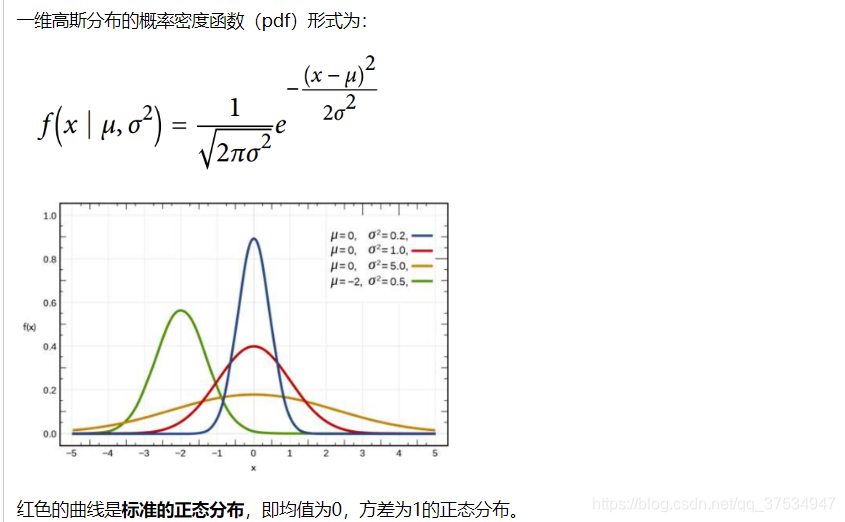
二维正态分布/多维正态分布

各向同性正态分布

注：即方差都是一样的，均值不一样，方差的值可以单独用标量表示。

多元/多维高斯/正态分布概率密度函数推导 (Derivation of the Multivariate/Multidimensional Normal/Gaussian Density)

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/（大佬大佬！！）

当年在学《概率论与数理统计》时，遇到二元正态分布的概率密度函数，那个公式特别长，当时只是要求记住，并未深究其原因，今天终于有机会好好回顾一下了。二元/二维只是多元的一个特例，现在将问题延伸到多元/多维高斯/正态分布概率密度函数的推导上。多元高斯分布在很多场景下都有用，比如高斯混合模型(Gaussian Mixture Model)中，每个组件都是单个多元高斯分布，样本不仅是一维的，现实中大多是数据样本都是多维的。只有真正弄清楚公式的来龙去脉，来能更好的编写程序，进行实现(虽然很多包都是现成的，不需要自己从头编写)。想要推导概率密度函数公式，需要知道线性代数中矩阵论的一些基础知识，从单变量到二元/二维再延伸到多元/多维，本身就涉及到从标量到向量再到矩阵的一个过程。这篇博客详细推导了多元/多维高斯/正态分布概率密度函数公式，并应用到二维高斯分布中，进行进一步分析。也给出了当维度之间独立同分布(Independent identically distributed, i.i.d.)情况下多维高斯分布的概率密度函数的特例。值得注意的是，整个过程仅是对一个样本进行计算，该样本无论是一个标量，还是一个多维向量，最终出来的概率密度函数都是一个数(标量)。如果有N个样本(按列排开)的话，其概率密度函数就是N维列向量。

注意：多元就是多维，高斯分布就是正态分布。(只是大概推导，过程可能并不严谨，望海涵)

1 前提基础

　　包括连续随机变量变换法(Transformations of Continuous Random Variables)，单变量正态分布的概率密度函数(Univariate Normal Density)，以及随机变量间的独立性(Independence of Random Variables)。