原题链接:https://www.luogu.com.cn/problem/P5937
题意解读:已知长度为n的01序列,给出m个判断,每个判断认为l~r之间1的个数是偶数或者奇数,计算前多少个判断是正确的。
解题思路:
先用前缀和思想来思考本题:假设s[i]是序列前i个数的和
对于每一个判断,有两种可能
第一、l~r有偶数个1,则有s[r]-s[l-1]是偶数,则有s[r]与s[l-1]同奇或者同偶
第二、l~r有奇数个1,则有s[r]-l[l-1]是奇数,则有s[r]与s[l-1]奇偶性不同
那么问题就转换成了,给定m个判断,每个判断是关于l-1和r之间的奇偶性关系,计算前多少个判断是正确的。
由于l、r的取值范围较大,首先需要进行离散化处理
1、离散化
struct node
{int l, r;string type;
} a[N];
int s[N * 2], cnt; //用于离散化的数组
map<int, int> h; //用于离散化的map
//离散化
int idx = 0;
sort(s + 1, s + cnt + 1);
for(int i = 1; i <= cnt; i++)
{if(!h.count(s[i])) h[s[i]] = ++idx;
}
for(int i = 1; i <= m; i++)
{a[i].l = h[a[i].l];a[i].r = h[a[i].r];
}要处理元素之间的关系,并判断关系是否正确,可以借助于并查集,通常有两种方法:带权并查集、扩展域并查集。
2、带权并查集
所谓带权并查集,就是在并查集中维护元素与其根节点之间的权值,可以通过一个数组d[N]来表示,d[x]表示节点x到父节点p[x]的权值
如何通过权值表示节点之间的关系呢?
比如:设元素x,d[x]=0表示x与其父节点奇偶性相同,d[x]=1表示x与其父节点奇偶性不同
d[x]在并查集路径压缩时要进行更新:
int find(int x)
{if(p[x] != x){int tmp = find(p[x]);d[x] = (d[x] + d[p[x]]) % 2; //把d[x]表示到父节点的权值更新为到根节点的权值,由于权值只有0和1,所以%2p[x] = tmp;}return p[x];
}知道了每个元素与其父节点之间的关系,那么两个元素之间的关系如何确定呢?
如果x,y在同一个集合中,d[x]、d[y]已经在路径压缩是更新成x、y到根节点的权值,有以下4点结论:
a、如果x与根节点奇偶性相同,y与根节点奇偶性相同,那么x,y奇偶性相同
b、如果x与根节点奇偶性相同,y与根节点奇偶性不同,那么x,y奇偶性不同
c、如果x与根节点奇偶性不同,y与根节点奇偶性相同,那么x,y奇偶性不同
d、如果x与根节点奇偶性不同,y与根节点奇偶性不同,那么x,y奇偶性相同
所以,对于条件:l r even来说,
设x=l-1,y=r,x的父节点为px,y的父节点为py
可以首先判断x和y是否在同一个集合
如果在同一个集合
则判断d[l-1]与d[r]之间的关系是否表示奇偶性相同,奇偶性相同意味着d[l-1]==d[r],如果不相等,说明产生矛盾
如果不在同一个集合
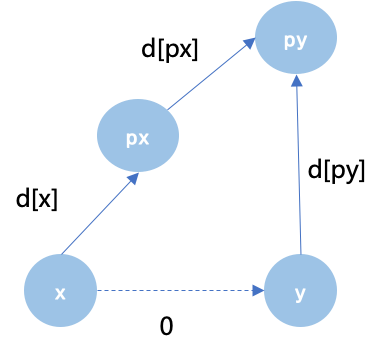
则进行集合合并,设将px合并到py上,为了维护元素之间的奇偶性关系,还要更新d[px],如下图,由于x,y奇偶性相同,那么x到y的虚拟权值是0,x到px的权值之和d[x]+d[px]等于0+d[py],因此d[px] = (d[py] - d[x] + 2) % 2,+2再%2是为了避免负数。
同理,对于条件:l r odd来说,
设x=l-1,y=r,x的父节点为px,y的父节点为py
可以首先判断x和y是否在同一个集合
如果在同一个集合
则判断d[l-1]与d[r]之间的关系是否表示奇偶性不同,奇偶性不同意味着d[l-1]!=d[r],如果相等,说明产生矛盾
如果不在同一个集合
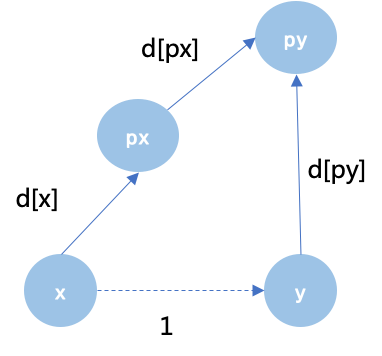
则进行集合合并,设将px合并到py上,为了维护元素之间的奇偶性关系,还要更新d[px],如下图,由于x,y奇偶性相同,那么x到y的虚拟权值是1,x到px的权值之和d[x]+d[px]等于1+d[py],因此d[px] = (1 + d[py] - d[x] ) % 2。
100分代码:
#include <bits/stdc++.h>
using namespace std;const int N = 5005;
int n, m;
struct node
{int l, r;string type;
} a[N];
int s[N * 2], cnt; //用于离散化的数组
map<int, int> h; //用于离散化的map
int p[N * 2], d[N * 2]; //p:并查集 d:每个元素到父节点的权值%2int find(int x)
{if(p[x] != x){int tmp = find(p[x]);d[x] = (d[x] + d[p[x]]) % 2;p[x] = tmp;}return p[x];
}int main()
{cin >> n >> m;for(int i = 1; i <= m; i++) {cin >> a[i].l >> a[i].r >> a[i].type;s[++cnt] = a[i].l;s[++cnt] = a[i].r;}//离散化int idx = 0;sort(s + 1, s + cnt + 1);for(int i = 1; i <= cnt; i++){if(!h.count(s[i])) h[s[i]] = ++idx;}for(int i = 1; i <= m; i++){a[i].l = h[a[i].l];a[i].r = h[a[i].r];}//并查集初始化for(int i = 1; i <= cnt; i++) p[i] = i;int ans = m;//处理for(int i = 1; i <= m; i++){int x = a[i].l - 1, px = find(x);int y = a[i].r, py = find(y);if(a[i].type == "even") //x、y同奇、偶{if(px == py) //已经在同一个集合{if(d[x] != d[y]) //x,y到根节点权值不相等,表示奇、偶不同,产生矛盾{ans = i - 1;break;}}else //合并x、y{p[px] = py;d[px] = (d[y] - d[x] + 2) % 2;}}else if(a[i].type == "odd") //x、y不同奇、偶{if(px == py){if(d[x] == d[y]) //x,y到根节点权值相等,表示奇、偶相同,产生矛盾{ans = i - 1;break;}}else{p[px] = py;d[px] = (1 + d[y] - d[x]) % 2;}}}cout << ans;return 0;
}3、扩展域并查集
带权并查集的本质是通过节点与根节点的权值关系来判定节点之间的关系,如果不够直观,下面介绍一种更容易理解的方法:扩展域并查集,又叫做种类并查集。
由于要将每一个元素是偶数、奇数两种情况都存储下来,需要将并查集长度进行扩展,此题元素有两种状态,只需要扩展2倍长度。
对于一个元素x,可以定义两个条件:x是偶数,x+cnt是奇数,
对于一个元素y,也可定义两个条件:y是偶数,y+cnt是奇数,
这样,
在遇到一组判断l r even时,令x=l-1,y=r,如果find(x)==find(y+cnt)则表示有矛盾,然后将"x是偶数 y是偶数"加入集合,将"x+cnt是奇数,y+cnt是奇数"加入集合
在遇到一组判断l r odd时,令x=l-1,y=r,如果find(x)==find(y)则表示有矛盾,然后将"x是偶数 y+cnt是奇数"加入集合,将"x+cnt是奇数 y是偶数"加入集合
100分代码:
#include <bits/stdc++.h>
using namespace std;const int N = 5005;
int n, m;
struct node
{int l, r;string type;
} a[N];
int s[N * 2], cnt; //用于离散化的数组
map<int, int> h; //用于离散化的map
int p[N * 4]; //p:并查集,扩展两倍长度int find(int x)
{if(p[x] != x) p[x] = find(p[x]);return p[x];
}int main()
{cin >> n >> m;for(int i = 1; i <= m; i++) {cin >> a[i].l >> a[i].r >> a[i].type;s[++cnt] = a[i].l;s[++cnt] = a[i].r;}//离散化int idx = 0;sort(s + 1, s + cnt + 1);for(int i = 1; i <= cnt; i++){if(!h.count(s[i])) h[s[i]] = ++idx;}for(int i = 1; i <= m; i++){a[i].l = h[a[i].l];a[i].r = h[a[i].r];}//并查集初始化for(int i = 1; i <= 2 * cnt; i++) p[i] = i;int ans = m;//处理for(int i = 1; i <= m; i++){int x = a[i].l - 1, y = a[i].r;if(a[i].type == "even") //x、y同奇、偶{if(find(x) == find(y + cnt)){ans = i - 1;break;}p[find(x)] = find(y);p[find(x + cnt)] = find(y + cnt);}else if(a[i].type == "odd") //x、y不同奇、偶{if(find(x) == find(y)){ans = i - 1;break; }p[find(x)] = find(y + cnt);p[find(x + cnt)] = find(y);}}cout << ans;return 0;
}