张昆玮线段树

介绍

非递归线段树实现方法，码量较短。

zkw 线段树的构造原理：

普通线段树采用堆存储，zkw线段树 本质上是满二叉树（若没有该区间则为空点）

但根据实际情况，原区间不一定构成满二叉树，据查询方式限制，空间开到最接近的 \(2^n\)（据性质树值域 = 底层节点数），即不存在的点有虚点填充。

既然不存在区间也需用空点填充，zkw线段树 对比 普通线段树 空间较大？

相比于普通线段树的结构混乱，一般开到 4 倍空间，而 zkw线段树 则只大约开到 3 倍空间

普通线段树本质上是从上往下搜索，从根节点向下操作。

zkw 线段树不同于普通线段树，本质上是从下往上搜索，从叶子节点向上操作。

zkw 线段树的基本操作

建树操作：

while (m <= n) {m <<= 1;
}
for (int i = m + 1; i <= m + n; ++ i) {tr[i] = read ();
}
m -= 1;
while (m --) {solve ();
}

维护区间和：\(\tt tr[] \rightarrow sum[]\)

solve () : sum[i] = sum[i << 1] + sum[i << 1 | 1];

维护区间最小值：\(\tt tr[] \rightarrow minn[]\)

solve () : minn[i] = min (minn[i << 1], minn[i << 1 | 1]); // 不支持修改

solve () : minn[i] = min (minn[i << 1], minn[i << 1 | 1]);
minn[i << 1] -= minn[i];
minn[i << 1 | 1] -= minn[i];

维护区间最大值：\(\tt tr[] \rightarrow maxx[]\)

solve () : maxx[i] = max (maxx[i << 1], maxx[i << 1 | 1]); // 不支持修改

solve () : maxx[i] = max (maxx[i << 1], maxx[i << 1 | 1]);
maxx[i << 1] -= maxx[i];
maxx[i << 1 | 1] -= maxx[i];

单点查询：

沿根节点向叶子节点累计加和

ll total = 0;
for (int i = id + m; i; i >>= 1) {total += minn[i]; 
}

单点修改：

修改当前节点并更新父亲节点

tr[id = id + m] += v;
while (m) {solve ();m >>= 1;
}

维护区间和：\(\tt tr[] \rightarrow sum[]\)

solve () : sum[i] = sum[i << 1] + sum[i << 1 | 1];

维护区间最小值：\(\tt tr[] \rightarrow minn[]\)

solve () : minn[i] = min (minn[i << 1], minn[i << 1 | 1]); // 不支持修改

solve () : minn[i] = min (minn[i << 1], minn[i << 1 | 1]);
minn[i << 1] -= minn[i];
minn[i << 1 | 1] -= minn[i];

维护区间最大值：\(\tt tr[] \rightarrow maxx[]\)

solve () : maxx[i] = max (maxx[i << 1], maxx[i << 1 | 1]); // 不支持修改

solve () : maxx[i] = max (maxx[i << 1], maxx[i << 1 | 1]);
maxx[i << 1] -= maxx[i];
maxx[i << 1 | 1] -= maxx[i];

区间查询

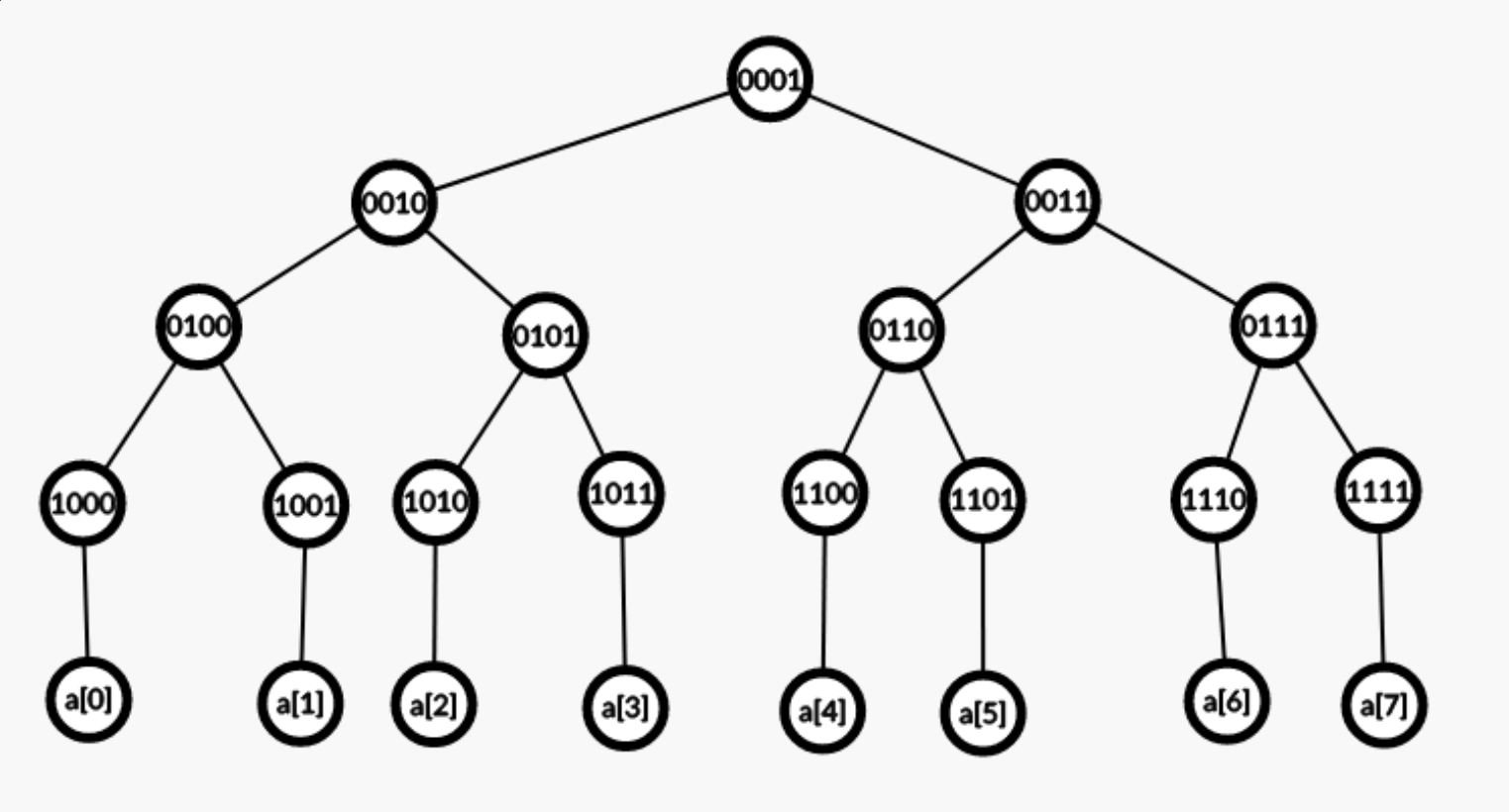
图片来源于网络（https://csacademy.com/app/graph_editor/）

假定先需查询区间 \([1,4]\) 那么操作如下：

1. 闭区间改开区间：\([1,4] \rightarrow (0,5)\) 扩增至 \((M + 0, M + 5) = (8,13)\)
2. 判断：左端点 \(1000\) 为 左儿子，其兄弟节点必在区间内，累加 \(total += D[1001_B]\)；判断：右端点 \(1101\) 为右儿子，其兄弟节点必在区间内，累加 \(total += D[1101_B]\)
3. 缩小区间：\(\tt l >>= 1\) \(\rightarrow\) \(\tt 1000_B >> 1 = 0100_B,\) \(\tt r >>= 1\) \(\rightarrow\) \(\tt 1101_B >> 1 = 0110_B\)
4. 判断：左端点 \(0100\) 为 左儿子，其兄弟节点必在区间内，累加 \(total += D[0101_B]\)；判断：右端点 \(1101\) 为左儿子，不操作
5. 缩小区间：\(\tt l >>= 1\) \(\rightarrow\) \(\tt 0100_B >> 1 = 0010_B,\) \(\tt r >>= 1\) \(\rightarrow\) \(\tt 0110_B >> 1 = 0011_B\)
6. 此时 节点 \(\tt l\) 和 节点 \(\tt r\) 为兄弟节点，停止操作。

伪代码：

for (int l = 开区间左端点, r = 开区间右端点; l, r 不是兄弟节点; 缩小区间) {if (l 为左儿子) {total += c[l 的兄弟节点];}if (r 为右儿子) {total += c[r 的兄弟节点];}
}

维护区间和：

for (int l = l + m - 1, r = r + m - 1, l ^ r ^ 1; l >>= 1, r >>= 1) {if (~ l & 1) {total += c[l ^ 1];}if (r & 1) {total += c[r ^ 1];}
}

维护区间最小值：

ll L = 0, R = 0;
for (int l = l + m - 1, r = r + m - 1; l ^ r ^ 1; l >>= 1, r >>= 1) {L += minn[l], R += minn[r];if (~ l & 1) {L = min (L, minn[l ^ 1]);}if (r & 1) {R = min (R, minn[r ^ 1]);}
}
ll res = min (L, R);
while (l) {res += minn[l >>= 1];
}

维护区间最大值：

ll L = 0, R = 0;
for (int l = l + m - 1, r = r + m - 1; l ^ r ^ 1; l >>= 1, r >>= 1) {L += maxx[l], R += maxx[r];if (~ l & 1) {L = max (L, maxx[l ^ 1]);}if (r & 1) {R = max (R, maxx[r ^ 1]);}
}
ll res = max (L, r);
while (l) {res += maxx[l >> 1];
}

区间修改

咕了。