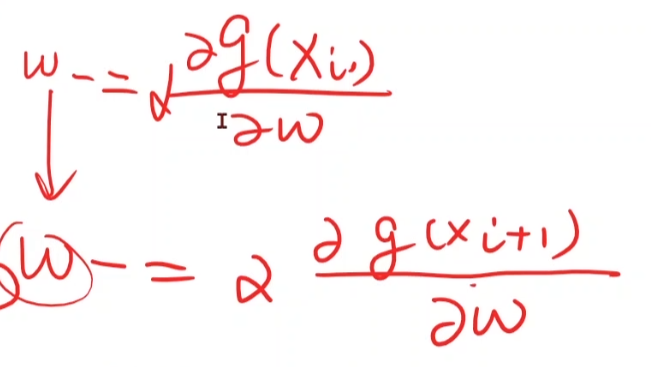外心
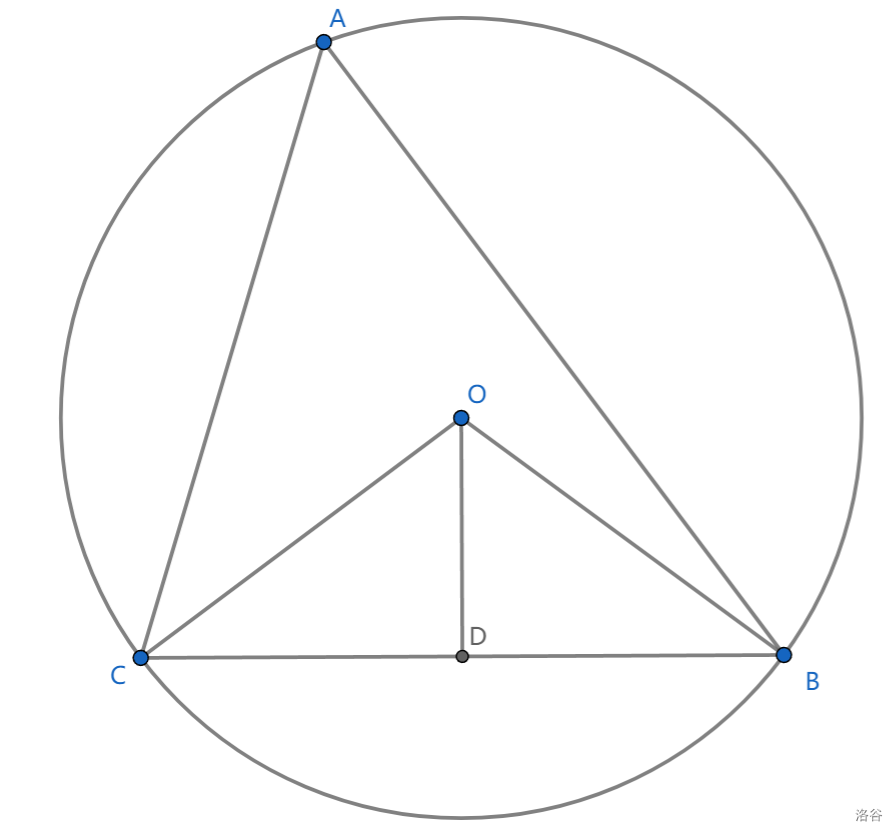
(这三条结论并不完全是平凡的)
1、 \(\angle BOC=2\angle A\)
2、 \(\angle CBO+\angle A=Rt \angle\)
3、 \(O\) 在三角形三边的中垂线上
例1
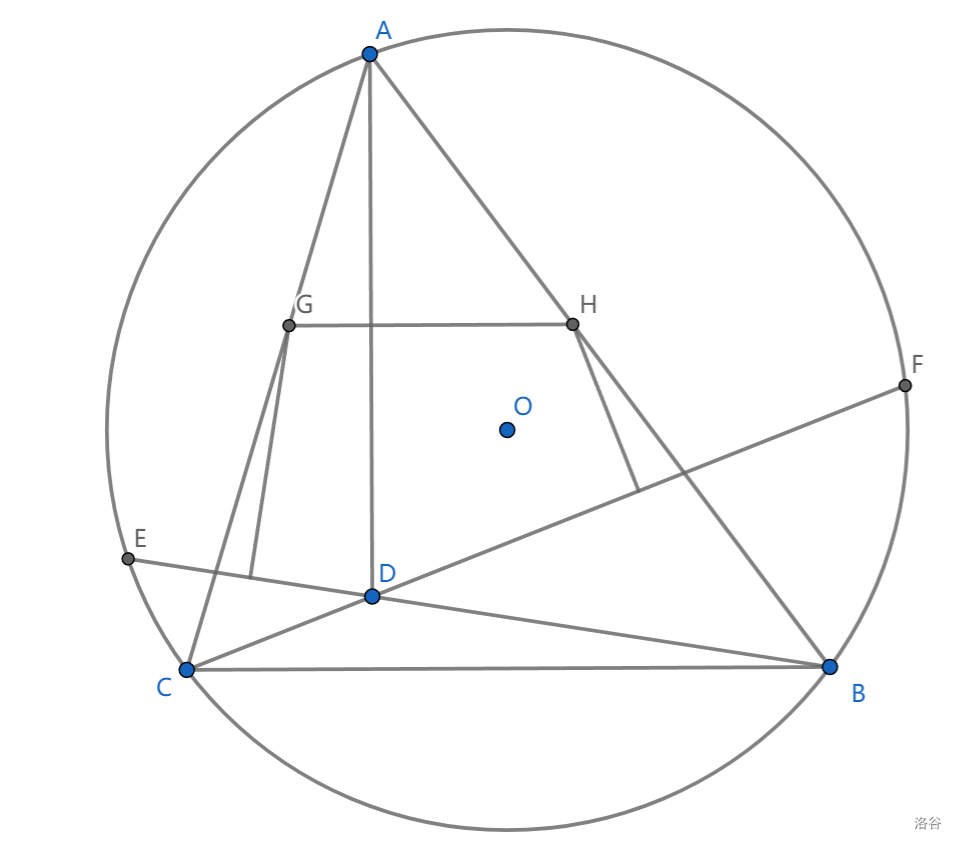
如图,\(\triangle ABC\) 内接于圆 \(O\) ,\(AD\perp BC\) ,延长 \(CD,BD\) 交圆 \(O\) 于点 \(F,E\) ,作 \(DE,DF\) 中垂线交 \(AC,AB\) 于点 \(G,H\) ,证明 \(GH // BC\)
分析:注意到 \(GH\) 似乎是 \(AD\) 的中垂线,猜测 \(G,H\) 为外心
考虑外心的刻画。在这里,最适合的是使用性质2,即 \(\angle DAH+\angle AFD=Rt\angle\) ,这里恰好不会用到点 \(H\) ,从而可证 \(G,H\) 为外心
例2
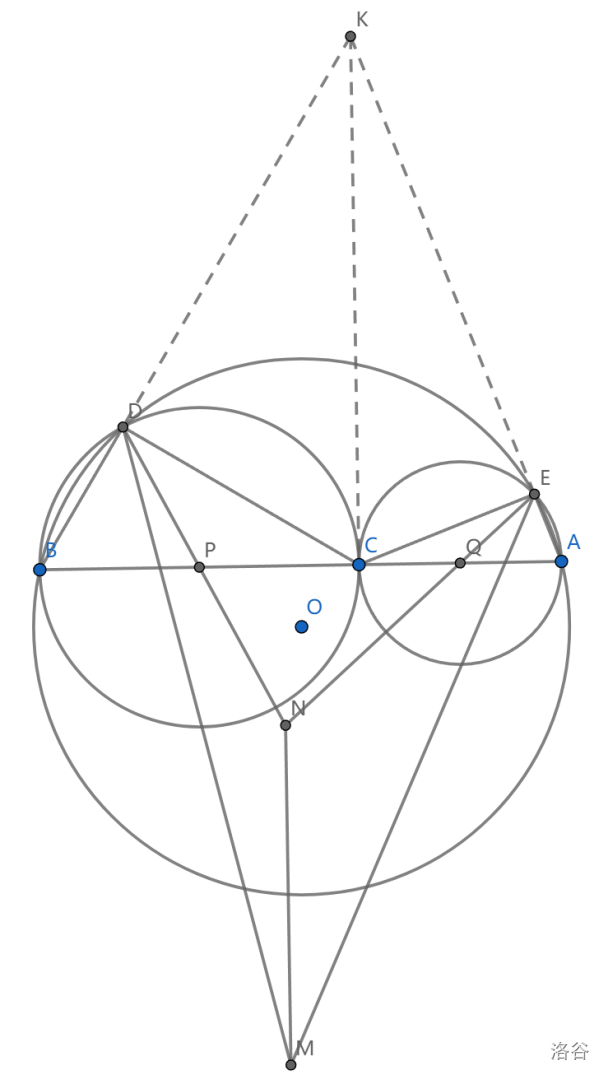
如图,\(AB\) 为圆 \(O\) 的弦,\(C\) 在 \(AB\) 上, \(D,E\) 在圆 \(O\) 上且满足 \(\angle BDC=\angle AEC=Rt\angle\) , \(P,Q\) 为 \(BC,AC\) 中点,延长 \(DP,EQ\) 交于点 \(N\) , \(\angle BDC\) 与 \(\angle AEC\) 的内角平分线交于点 \(M\) ,证明: \(MN\perp AB\)
首先由三个圆不难联想到构造根心,得到点 \(K\) ,有 \(CK\perp AB\) 及 \(K,E,C,D\) 共圆
同时可以注意到 \(NE=ND\) ,因为 \(\angle NDE=\angle CDN+\angle CDE=\angle CKB+\angle CKE=\angle AKB\) , \(\angle NED\) 同理
事实上, \(\angle EMD=\angle END-(\angle NEM+\angle NDM)\) ,不难得到其与 \(\angle NEF\) 互余,即 \(N\) 为 \(EFM\) 外心
然后随便导角都可以出来
垂心
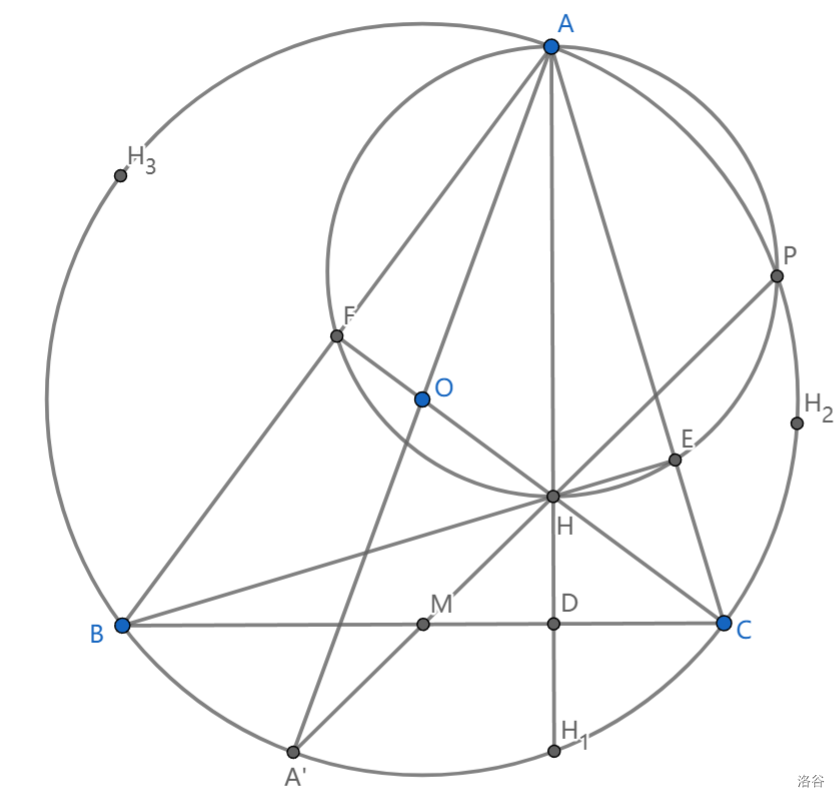
1、\(H\) 为 \(\triangle DEF\) 内心
2、(鸭爪定理)\(H\) 关于三边对称点在外接圆上
3、\(AH\cdot HD=BH\cdot HE=CH\cdot HF\) (可用于反演)
4、\(\triangle ABC,\triangle BCH\) 等三角形的外接圆半径相等
5、\(AH=2OM\) ,其中 \(\angle BAO=\angle CAH\)
6、\(MH\) 与外接圆交点 \(A',P\) 满足 \(A'\) 为 \(A\) 对径点且 \(A'M=MH\),\(AFHEP\) 共圆
7、\(O,H\) 为等角共轭点
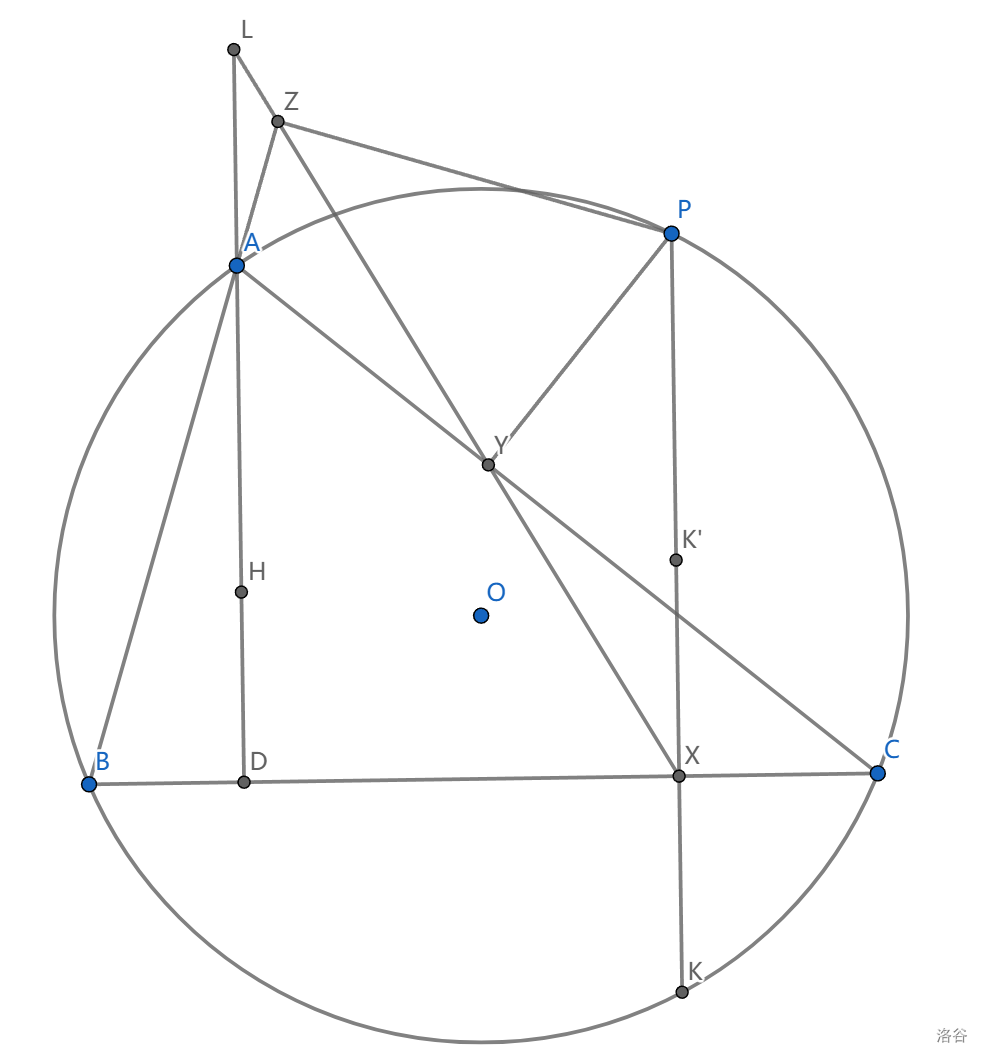
8、对弧 \(BC\) 上任一点 \(P\) , \(PH\) 平分点 \(P\) 关于 \(\triangle ABC\) 的西姆松线
这个结论的证明需要引理(其实可以不用,但是我们想发掘这个构型的更多性质:
9、圆内接四边形 \(ABCD\) 中, \(X,Y\) 分别是 \(\triangle ABC,\triangle BCD\) 的垂心,则 \(AXYD\) 是平行四边形
这个可以用鸭爪定理得到一个等腰梯形后轻松证明。
我们说 \(K\) 关于 \(BC\) 的对称点 \(K'\) 是 \(\triangle PBC\) 的垂心,即鸭爪定理的逆定理(最好说是导角),所以 \(AHK'P\) 是平行四边形
西姆松线上显然有 \(PXYC\) 共圆,用 \(Reim\) 引理可以看到 \(AK//LX\) ,同时 \(LA//XK\) ,所以有平行四边形 \(ALXK\) ,则 \(AL=XK=XK'\)
结合两个条件可知 \(LH=XP,LH//XP\) ,完成了证明。
例1
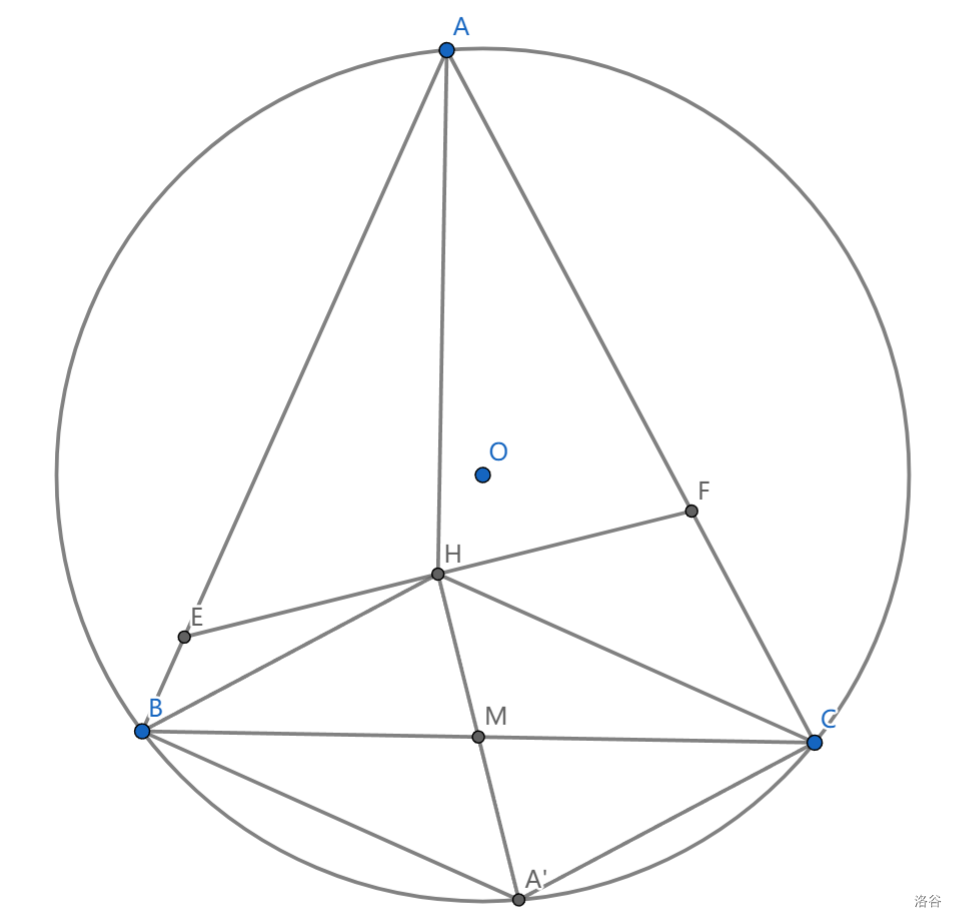
如图,\(M\)为 \(BC\) 中点, \(EF\perp HM\) ,求证:\(EH=HF\)
这个构型比较常见,实际上可以证明 \(\frac{EH}{FH}=\frac{BM}{CM}\)
\(\angle MCH=\angle HAE\)
又 \(AE\perp CH,HM\perp EF\) ,可知\(\angle AEH=\angle CHM\)
从而 \(\triangle AEH\sim \triangle CHM\)
同理 \(\triangle AFH\sim \triangle BHM\)
接下来利用垂心的性质,还能看到很明显的全等 \(\triangle BHM\overset{\backsim}{=} \triangle CA'M\) ,可知 \(\triangle CA'H\sim\triangle AFE\)
那么就有 \(CFHA'\) 共圆,同理 \(BEHA'\) 共圆
可知 \(\angle HFA'=\angle HCA'=\angle HBA'=\angle HEA'\)
即 \(A'H\) 为 \(EF\) 中垂线,这就做完了。
例2
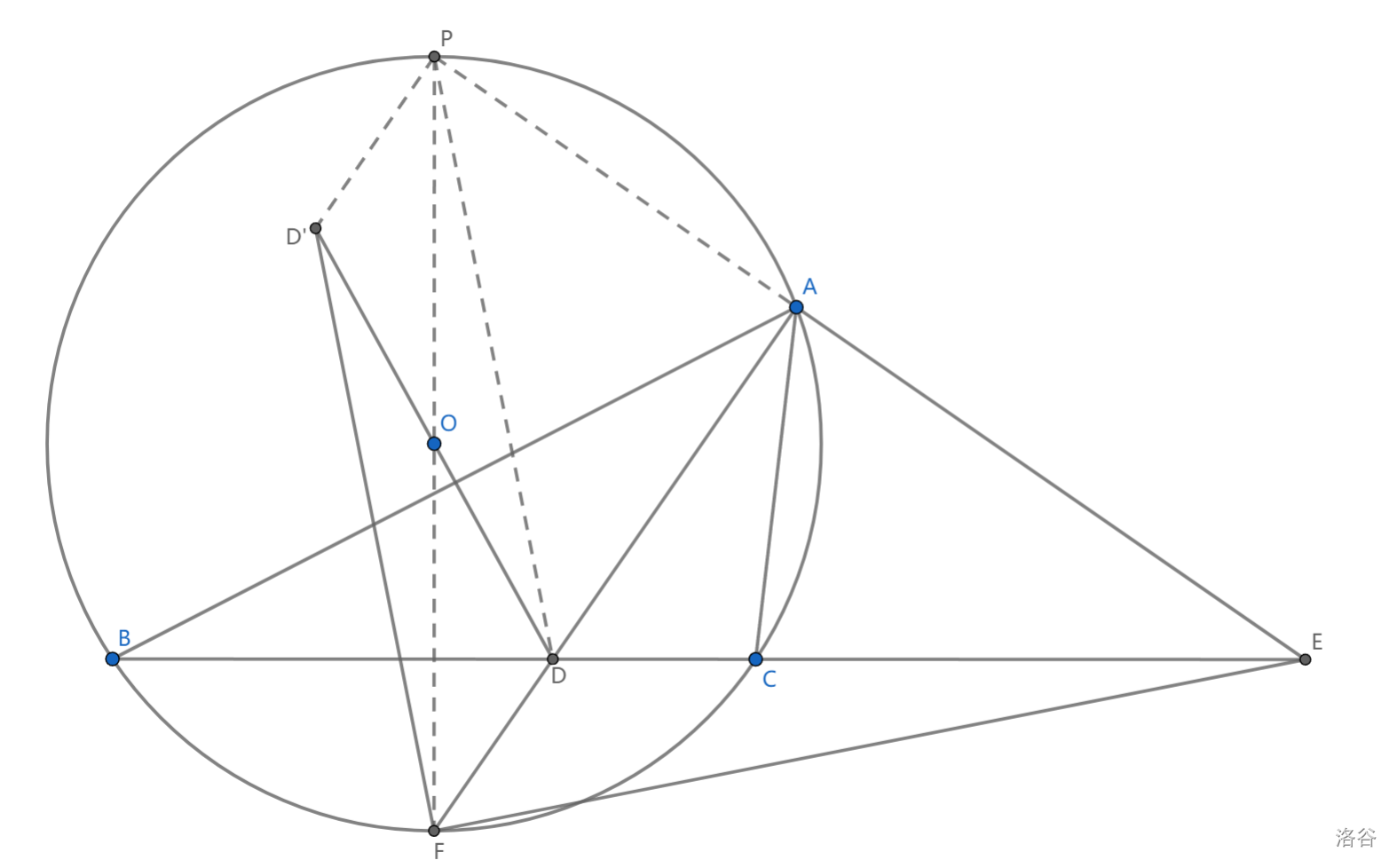
如图, \(\triangle ABC\) 内接于圆 \(O\) ,\(\angle BAC\) 内外角平分线分别交 \(BC\) 于 \(D,E\) , \(F\) 为弧 \(BC\) 中点, \(D'\) 为 \(D\) 关于点 \(O\) 对称点,求证: \(D'F\perp FE\)
处理对称点有什么方法呢?可能很多,不过这里是关于点 \(O\) 的对称点,这可不错,我们可以再找一些圆上的点,然后得到一些对径点。
构造 \(F\) 关于 \(O\) 对称点 \(P\) ,由 \(FP\) 为直径, \(\angle PAF=Rt\angle\) ,可知 \(PAE\) 共线
本题更关键的部分是发现 \(ED\perp PF,FD\perp PE\) ,即 \(D\) 为 \(\triangle PEF\) 垂心,则 \(PD\perp EF\)
又 \(PDFD'\) 为平行四边形,所以 \(D'F\perp FE\)
总是应当敏锐地发现一些特殊的点(而不是说,题目循规蹈矩地构造出来了某个特殊点,你才能发现)
例3
九点圆
基于鸭爪定理,关于 \(H\) 对外接圆进行比例 \(2:1\) 的位似,我们会得到垂足三角形的外接圆。
这个圆上还有 \(AH,BH,CH\) 的中点和 \(\triangle ABC\) 三边中点,被称为九点圆。
同时 \(OGH\) 是共线的,满足 \(OG:GH=1:2\)
例1
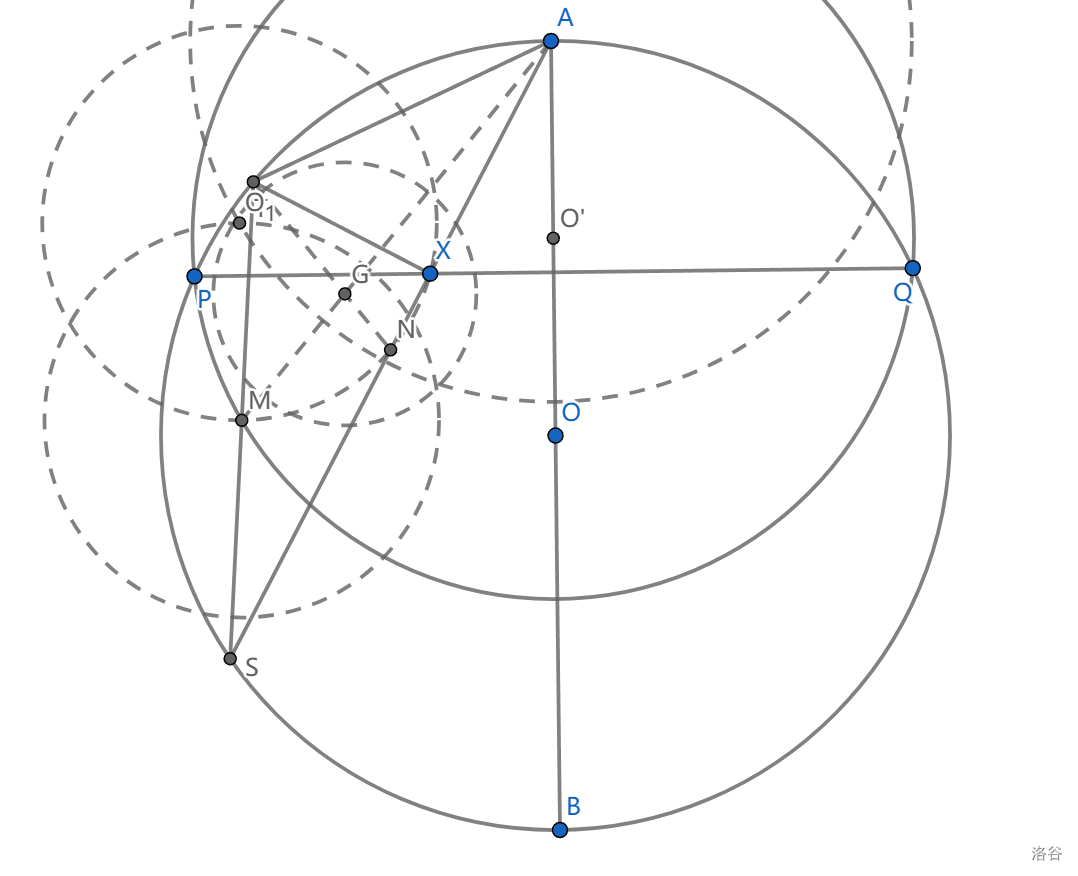
如图, \(AB\) 是 \(\odot O\) 直径, \(P,Q\) 是圆上关于 \(AB\) 对称的两点,满足 \(AP<BP\) , \(X\) 是线段 \(PQ\) 上的动点, \(T\) 是弧 \(AQB\) 上满足 \(XT\perp AX\) 的一点。设 \(M\) 是弦 \(ST\) 的中点。当 \(X\) 在 \(PQ\) 上移动时,求证: \(M\) 在定圆上。
这题可以直接找特殊情况,然后发现圆,直接计算即可。下面是一种纯几何做法。
我们作 \(AST\) 的九点圆(这无疑是需要勇气的),设出 \(AS\) 中点 \(N\) 。由 \(A\) 是弧中点,熟知 \(AX\cdot AS=\frac 14 PQ^2\) ,从而 \(AX\cdot AN\) 是定值, \(A\) 关于九点圆的圆幂是定值,所以九点圆圆心 \(O_1\) 在定圆 \(A\) 上。
接下来关于圆心 \(O\) 对这个定圆作位似,位似比为 \(\frac 23\) ,将 \(O_1\) 变为 \(\triangle AST\) 的重心 \(G\) , \(G\) 在定圆上
再关于 \(A\) 对这个定圆做位似比为 \(\frac 32\) 的位似,现在 \(M\) 在定圆上。
例2
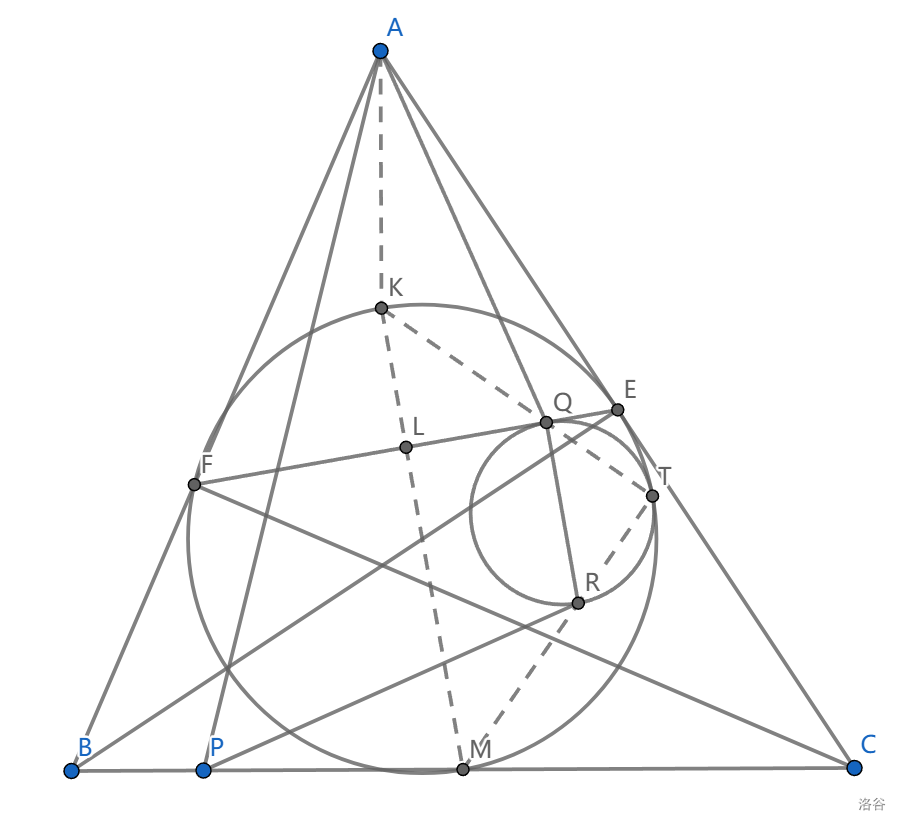
如图, \(BE,CF\) 是 \(\triangle ABC\) 的两条高,点 \(P\) 和 \(Q\) 分别在线段 \(BC,EF\) 上, \(\angle BAP=\angle CAQ\) ,点 \(R\) 满足 \(PR\perp AQ,QR\perp EF\) ,求证:以 \(QR\) 为直径的圆与 \(\triangle ABC\) 相切。
相切即关于切点位似,我们找到 \(QR\) 对应的直径 \(KM\) (与 \(EF\) 垂直),然后证明 \(KQ\cap MR\) 在两圆上,这等价于说 \(KQ\perp MR\)
直接处理这两条线看上去就毫无希望,于是我们看看条件 \(PR\perp AQ\) ,结合 \(AK\perp PM\) ,我们似乎应当将这两条线放入 \(\triangle AKQ\sim \triangle PMR\) 然后另两条边对应垂直就能给出这个垂直。
要证明这个相似,需要 \(\frac{AQ}{AK}=\frac{PR}{PM}\) ,前者看上去还好,但计算后者是灾难性的工作, \(PR\) 尚未得到任何刻画。
我们只能用同一法,我们将定义 \(T=KQ\cap \odot_{KM直径}\) ,然后设 \(R'=QR\cap MT\) (注意 \(QR\) 与 \(R\) 无关)(将它脱离 \(PR\) ,然后用点 \(T\) 生成)
在这样的条件下,我们有 \(KT\perp MT\) ,于是 \(MR'\perp KQ\) ,则对应边垂直给出 \(\triangle MR'P\sim \triangle KQA\)
我们要证 \(R'\in \odot_{QR直径}\) ,也就是 \(\angle QTR'=Rt\angle\)
我们还没利用过等角线的条件,这个条件说明 \(P,Q\) 是 \(\triangle AEF\sim\triangle ABC\) 的对应点,然后导比例(这个结论不像是能导角导出来的,实际上,我们的相似用角关系生成,应当给出比例关系)
通过线段证明垂直有不少的方法,而这里最优的很明显是我们证明 \(\triangle KLQ\sim\triangle KTM\) ,于是我们要证明 \(\frac{MR'}{KQ}=\frac{LQ}{KL}\) (注意 \(QR'//KM\) )
我们先有 \(\frac{MR'}{KQ}=\frac{MP}{AK}\) ,然后利用相似对应有 \(\frac{MP}{LQ}=\frac{AC}{AF}=\frac{KF}{KL}=\frac{AK}{KL}\) ,马上得到想要的结果。