Two-Processor Scheduling 学习笔记

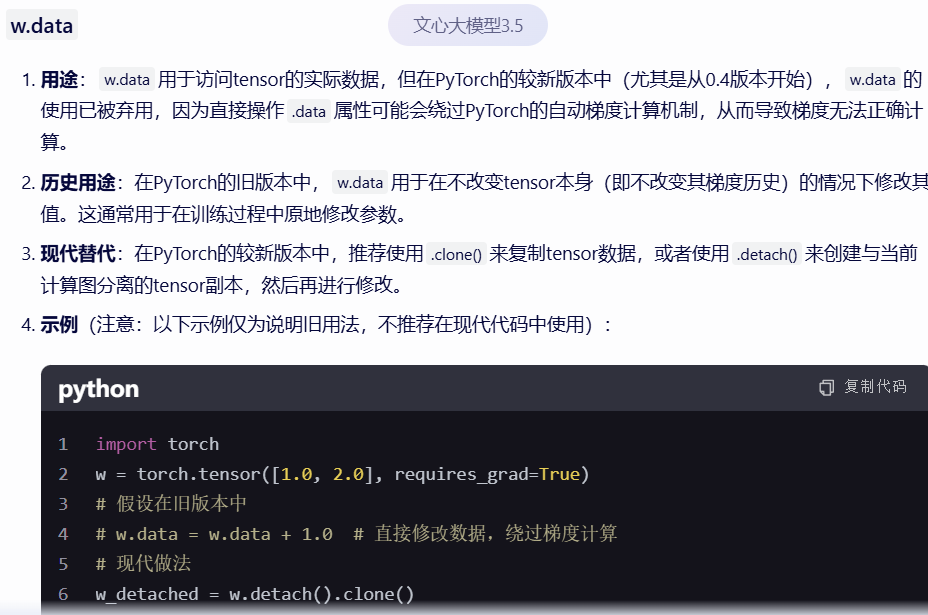
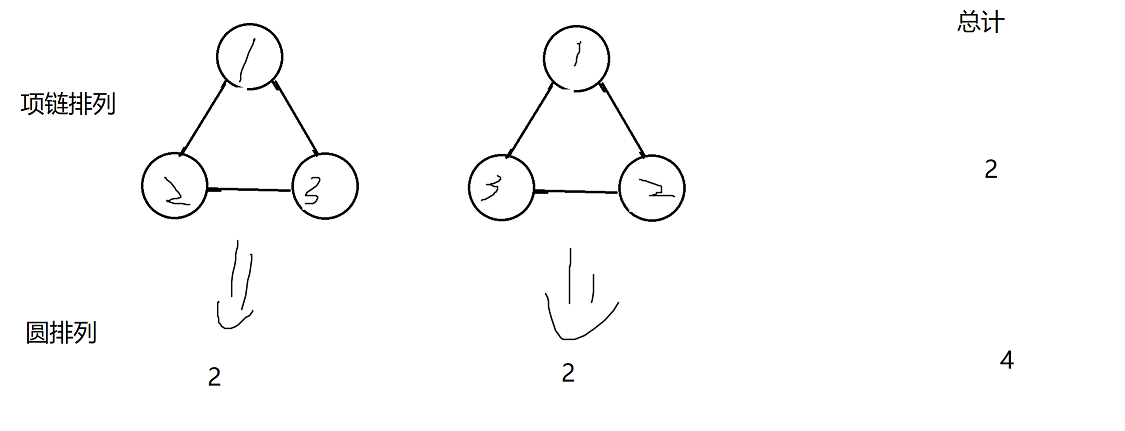
为什么有人联考放论文题啊？不过好有趣。参考的 glx 博客。

考虑这么一个问题，给定一张偏序图，即一个满足传递性和非自反性的偏序关系 \(\succ\) 连成的 DAG。你需要对这张图进行拓扑排序，每次可以同时删去一个或者两个零入度点，问最少删多少次可以把图删空并构造方案。

形式化地说，我们需要求出两个等长序列 \(a,b\)，满足 \(\forall i>j,a_i/a_i \not\succ a_j/b_j\) 以及 \(a_i \not\succ b_i,b_i \not\succ a_i\)，然后最小化这个序列的长度。这里 \(b_i\) 可以取空点 \(\emptyset\)。

先考虑怎么玩出答案，首先我们可以得到一些答案的下界。比如我们建一张图 \(G\)，如果 \(x \not\succ y,x \not\succ y\) 即 \(x,y\) 互不可达，我们就连一条边。那么删图 \(G\) 的最大匹配一定能导出一个下界，因为同时删去的点只能取 \(G\) 中的一条边。事实上这似乎就是答案，然而一方面一般图最大匹配太难求，另一方面这个东西无法直接导出方案，毕竟删 \(G\) 中的边不能保证都是零入度点。

我们考虑一些更松的上界，对于 \(G\) 中的每一个联通块我们求它的大小除以二上取整的和，显然这是最大匹配的一个上界，也就是答案的下界，记为 \(F(G)\)。我们考虑再在 \(G\) 中删去一些点得到 \(G'\)，你会发现 \(F(G')\) 有可能比 \(F(G)\) 还大，这也说明在 \(G\) 中删去一些点之后反而有可能得到一个更紧的下界。我们可以说明我们可以通过这种方式直接让这个下界等于答案并同时给出一个顶到下界的构造。

先考虑怎么构造。我们首先需要得到一个反拓扑序 \(P\)，记 \(\alpha(i)\) 表示 \(i\) 在 \(P\) 中的下标，记 \(N(u)=\{\alpha(v)|u\succ v\}\)，将每一个 \(N(u)\) 从大到小排成一个序列，我们需要令此拓扑序满足 \(N(P_i)\) 字典序不降。注意到如果 \(u\succ v\)，那么一定有 \(\alpha(u)> \alpha(v),N(u)\geq N(v)\)。所以我们只需要对反图拓扑排序，每次取出 \(N(x)\) 字典序最小的 \(x\) 即可构造出 \(P\)。

我们说我们维护一个队列，对反图拓扑排序时每取出一个点，扫描反图上的所有出边，将这些出边对应的点从队列中取出，然后按它们在队列中的相对顺序依次放到序列末尾。由于 \(N\) 从大到小排序，我们每取出一个点需要更新其所有前驱的 \(N\) 序列，这些 \(N\) 序列会变成所有 \(N\) 序列中最大的那一批。这个过程可以用队列或可删堆简单维护。

得到 \(P\) 之后，我们再对原图直接进行拓扑排序，每次优先同时删除 \(\alpha_i\) 最大的一个或两个点，就构造出了题意所要求的方案。

接下来考虑证明这为什么是一个最小的操作方案。我们设我们刚刚得到的操作序列为 \((a_1,b_1),(a_2,b_2)\dots (a_k,b_k)\)，定义 \(\alpha(\emptyset)=0\)，不妨令 \(\alpha(a_i)>\alpha(b_i)\)。我们可以发现 \(\alpha(a_i)>\alpha(a_{i+1})\)，否则的话，因为 \(\alpha(a_{i+1})\) 更大但我们在第 \(i\) 轮却没有取它，肯定是因为 \(a_i\succ a_{i+1}\) 或 \(b_i\succ a_{i+1}\)，这都会导出 \(\alpha(a_i)>\alpha(a_{i+1})\) 矛盾。

然后我们考虑对着操作序列分段，分段方式是这样的：首先 \(a,b\) 的最后一个元素一定是一段的末尾，我们记 \(a_k,b_k\) 为 \((p_1,q_1)\)。设我们找到的上一段的结尾为 \(p_i,q_i\)，然后我们往前找，直到找到第一个 \(\alpha(b_x)<\alpha(p_i)\)，令 \((a_x,b_x)\) 为新的段的末尾 \((p_{i+1},q_{i+1})\)。

注意到当 \(b_i=\emptyset\) 时，它一定会被作为段的结尾，那么这也就是说我们刚刚分的每一段除去末尾的 \(q_i\)，其它的一定是非空的。即下图中的绿色部分（蒯的图）。

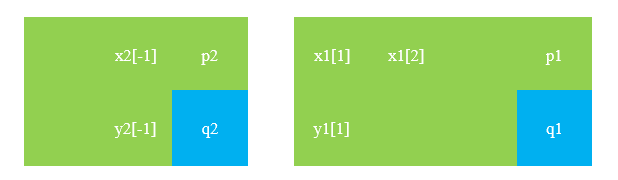
我们考虑记 \(G'=G/\{q_i\}\)，我们只需要说明我们刚刚操作序列分的每一段除去 \(q_i\) 后正好是 \(G'\) 中的若干个连通块的并，即说明 \(\forall x,y\notin \{q_i\}\)，\(x,y\) 不在同一段，那么就有 \(x\succ y\) 或 \(y\succ x\)。这样的话 \(F(G')\) 是一个下界，而这个操作序列明显达到了这个下界。

考虑为什么 \((p_2,q_2)\) 那里 \(\alpha(q_2)<\alpha(p_1)<\alpha(x1_i),\alpha(y1_i)\) 但为什么先选了 \(q_2\)，这肯定是因为 \(p_2\succ x1_i,y1_i\)，因为由于 \(\alpha(q_2)<\alpha(x1_i),\alpha(y1_i)\) 不可能有 \(q_2\succ x1_i,y1_i\)。

接下来只要说明 \((p_2,q_2)\) 那个段里除了 \(q_2\) 其余的全都可以到达 \(p_2\)。按字典序排的好处从这里体现出来了，由于 \(\alpha(x2_i),\alpha(y2_i)>\alpha(p_2)\)，所以 \(N(x2_i),N(y2_i)\geq N(p_2)\)，那么这些点要么能够到达 \(p_2\) 能到的所有点，要么直接能到达 \(p_2\) 本身，要么能到达一个更加靠后的 \(x2_j,y2_j\) 从而也能到达 \(x1_i,y1_i\) 的所有点。

综上所述，对于相邻两段绿色部分的每一对节点都是可达的。所以不同段的绿色部分的每一对节点两两可达，即在 \(G\) 中这些绿色部分是不联通的。于是就证明了操作次数顶到了下界！