给n个节点m条边,构造一些无向图,构造出来的图需要满足以下条件:
(1)图中没有自环
(2)图中每个点的度最大是2
(3)图中连通块大小最大为L
问能构造出多少个这样的图出来,答案可能很大,对1e9+7取模
输入格式
第一行三个整数n,m,L
2<=n<=300,1<=m,L<=n
输出格式
一个整数
输入/输出例子1
输入:
3 2 3
输出:
3
样例解释
无
在了解此题前,我们先学一些前置知识
前置知识
环和链的重复性
1.对于一个链,反转一下还是同一副图,例如:
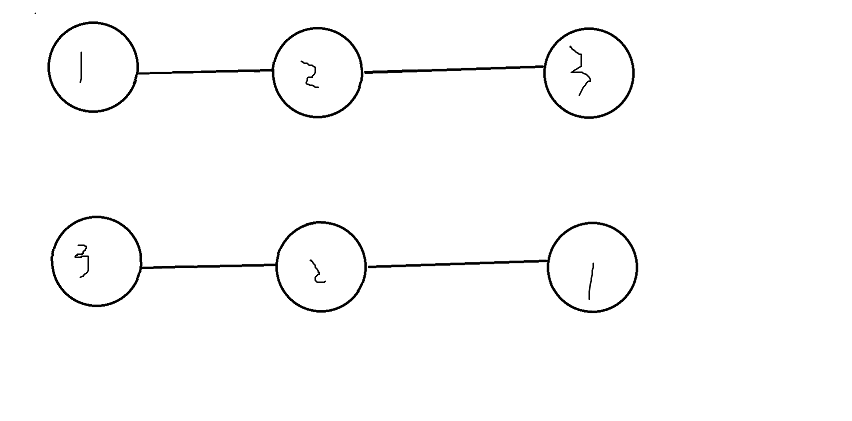
2.对于一个环,把图翻过来还是同一幅图
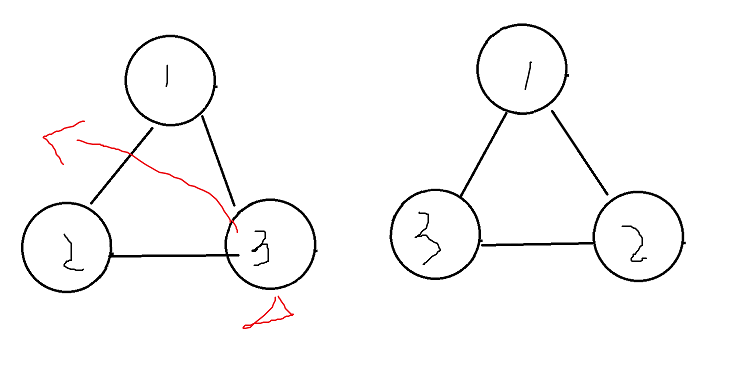
想成立体空间,把这个图反转过来,这样的图是同一个图
根据点数计算不同链的数量
对于一个链
n个节点,构成的不同图数量
n! / 2
很简单,因为会有重复,把链反转还是同一个链,所以结果要除二
根据点数计算不同环的数量(圆排列,项链排列)
映射思想
今天的第一个思想:运用映射思想
如果算A集合很难算,但我知道B集合有多少个,且B与A有关系,那么就可以用B映射A
例如,我们想求A集合内成员数量,但是正面无法算,可是我们知道B集合有5个成员,且1个A集合相当于5个B集合,那么A集合成员数量就可以通过B集合成员数量推出来,即 A集合数量=B集合数量*5 = 5*5 = 25
这里引入几个概念
圆排列
圆排列:对于n个节点能构成多少个不同的圆,注意是二维(2D)的,就是在一个二维平面,顺时针看不一样才算不同排列
正面算很难是吧,假设此时n=3
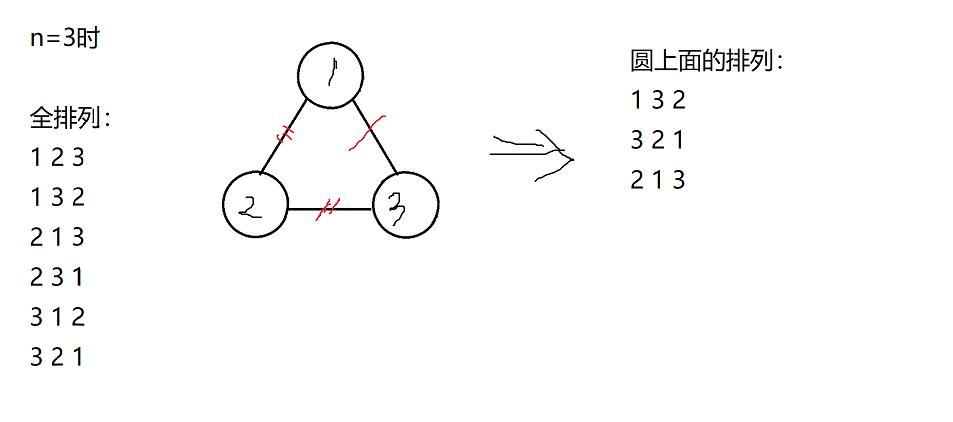
根据映射思想,我们可以算出全排列数量,即线性排列数量,很好算嘛,n! 种
然后我们再算一个圆(任意一个),它对应的排列数量,怎么求?我们可以先暂时割掉一个边,然后再dfs就出来顺序了,如上图
先割掉(1,3)这条边,我们dfs一遍,就是{1,2,3},那么这就是一个排列了,由于一共可以割掉n条边,所以有n种
一个圆对应这么多个排列数量,我们总共有那么多个排列数量,我们用总共/单个,不就算出来数量了吗
即 n! / n = (n-1)!
简化:假设有n个点,那么有n!种线性排列,有n个圆上面的排列(n个切割点)
至此推出了圆排列公式:(n-1)!
项链排列
项链排列:对于n个节点能构成多少个不同的圆,注意是二维(3D)的,就是在一个三维平面,顺时针看不一样也算同一个排列
假设有n个点,那么有n!种线性排列,有(n-1)!圆排列,我们观察一下圆排列和项链排列可以观察出一个规律:
假设n=3,那么这个项链排列有2个(固定着1,把图反转一下,运用空间想象力哈),根据圆排列计算公式,(n-1)!=(3-1)!=2!=2,那么把这些值加在一起就可以发现规律了!
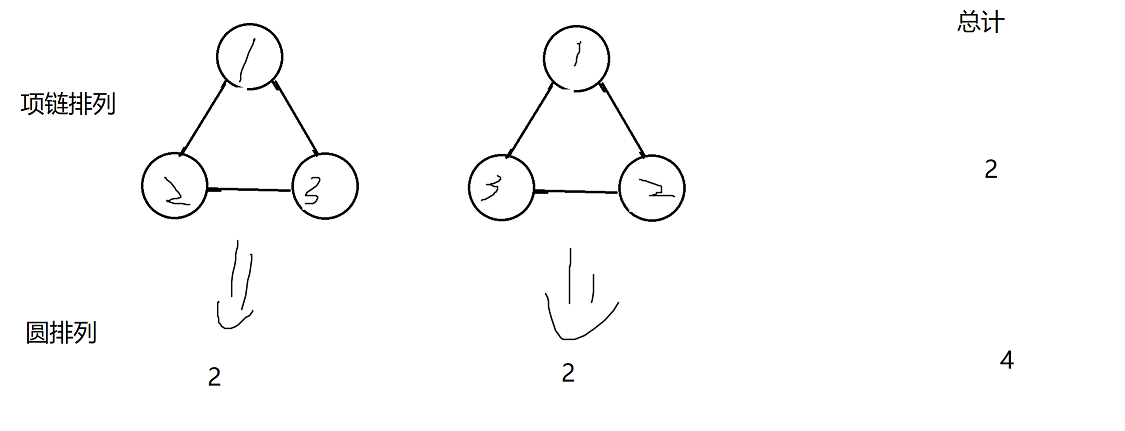
圆排列是项链排列的2倍
至此推出了项链排列公式:(n-1)! / 2
本题做法
根据题意,图会构成:
1) 一条链,边数=点数-1
2) 一个环,边数=点数
边数和点数有一种对应关系,我们dp定义关系只用点就ok
f[i][j]:当前图考虑了i个点,j条边
我们假设新加入k个点,和图原来的构成:
1)链的情况
现在加入k个点,相当于加入k-1条边
在他之前的图,有i-k个点,j-(k-1)条边
我们这k个点从总点数选对吧,那么有多少选择方法?
之前图的点数不可再选了
剩余的就是可以选的
总共可选点数 - 之前图的点数 即可
C(n-(i-k), k)
注意重复情况!我们选k个节点,我们分别考虑每个点
第一次:选1 2 3
第二次:选1 3 2
那不就重复了吗,要去重
技巧:相当于排序,有一种顺序,我们让最小点先进入选择的序列中,一定要放进去!这样就不重复了
那么此时相当于
C(n-(i-k)-1, k-1)
选出来后考虑如何排列
2)环的情况
现在加入k个点,相当于加入k条边
原来图点数 i-k,边数 j-k