P9520 [JOISC2022] 监狱

P9520 [JOISC2022] 监狱

题目描述

有一棵 \(N\) 个节点的树，有 \(M\) 个囚犯，要从 \(S_i\) 走到 \(T_i\)。每一时刻可以发布一个命令让一名囚犯走到相邻的节点，要求任意时刻囚犯不能走到同一个节点上，求是否可以令每一个囚犯从 \(S_i\) 走到 \(T_i\)。

做法解析

首先我们可以发现一个囚犯要么一次走完其路径，要么不走。

故我们需要确定一个走的先后顺序，这等价于对于任意两个囚犯，我们确定他们走的先后顺序。

我们考虑囚犯 \(A\)，\(B\)

• 如果，\(S_A\) 在 \(B\) 的路径上 那么 \(A\) 要先走。
• 如果，\(T_A\) 在 \(B\) 的路径上 那么 \(B\) 要先走。

我们考虑先走的囚犯向后走的囚犯连一条有向边，如果是一个 DAG 那么就可以找到一种满足条件的方案，否则不行。

直接连边是 \(O(n^2)\) 的，我们考虑 树链剖分 加 线段树优化连边。

我们需要两棵线段树，一棵 S树 表示起点，一棵 T树 表示终点。

• \(A\) 路径上的点（\(S_A\) 除外）在 S树 上的节点向 \(A\) 连边。
• \(A\) 向 \(A\) 路径上的点（\(T_A\) 除外）在 T树 上的节点连边。
• \(A\) 向 \(S_A\) 在 S树 上的节点连边。
• \(T_A\) 在 T树 上的节点向 \(A\) 连边。

对于 S树 子区间向父区间连边。

对于 T树 父区间向子区间连边。

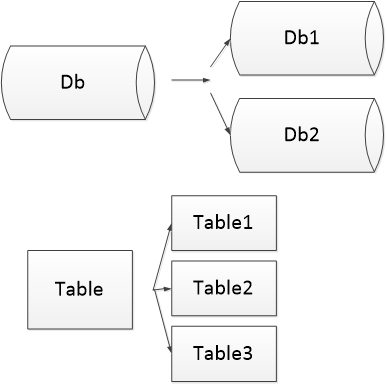
参见下图：

图片只说明建图方式，其不一定符合实际数据。

时间与空间复杂度 \(O(n log^2 n)\)。

注意事项

• 线段树虽然理论上只需要用 \(2n-1\) 个节点，但是如果使用普通的建树方式，节点的编号是 \(4n\) 级别的。

代码

然而实现的并不好。

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6;
const int maxm=1e7;
struct Edge{int u,v,nxt;};
int n,m;
int dg[maxn+5];
int hd[maxn+5],et;
Edge e[maxm+5];
int idt;
int de[maxn+5],sz[maxn+5],fa[maxn+5];
int sn[maxn+5],id[maxn+5],tp[maxn+5];
int S[maxn+5],st;
int stp,sts,stt,edp;
int V[maxn+5],vt;
inline void Adde(int u,int v){dg[v]++;e[et].u=u,e[et].v=v;e[et].nxt=hd[u],hd[u]=et++;
}
void Dfs1(int u){int v;sz[u]=1;for(int i=hd[u];~i;i=e[i].nxt){v=e[i].v;if(v==fa[u]) continue;fa[v]=u;de[v]=de[u]+1;Dfs1(v);sz[u]+=sz[v];if(sz[sn[u]]<sz[v]) sn[u]=v;}
}
void Dfs2(int u,int TP){int v;id[u]=++idt;tp[u]=TP;if(sn[u]) Dfs2(sn[u],TP);for(int i=hd[u];~i;i=e[i].nxt){v=e[i].v;if(v==fa[u]||v==sn[u]) continue;Dfs2(v,v);}
}
void Build(int x,int L,int R){if(L==R) return;else{int mid=(R-L)/2+L;Adde(sts+(x<<1),sts+x);Adde(sts+(x<<1|1),sts+x);Adde(stt+x,stt+(x<<1));Adde(stt+x,stt+(x<<1|1));Build(x<<1,L,mid);Build(x<<1|1,mid+1,R);}
}
void Query(int x,int L,int R,int l,int r){if(l<=L&&R<=r) V[++vt]=x;else{int mid=(R-L)/2+L;if(l<=mid) Query(x<<1,L,mid,l,r);if(mid<r) Query(x<<1|1,mid+1,R,l,r);}
}
inline void TQuery(int l,int r,int t){if(l<=t&&t<=r){if(l<t) Query(1,1,n,l,t-1);if(t<r) Query(1,1,n,t+1,r);}else Query(1,1,n,l,r);
}
void Modify(int p,int u,int v){int tu=id[u],tv=id[v];while(tp[u]!=tp[v]){if(de[tp[u]]<de[tp[v]]) swap(u,v);vt=0;TQuery(id[tp[u]],id[u],tu);for(int i=1;i<=vt;i++) Adde(sts+V[i],stp+p);vt=0;TQuery(id[tp[u]],id[u],tv);for(int i=1;i<=vt;i++) Adde(stp+p,stt+V[i]);u=fa[tp[u]];}if(de[u]<de[v]) swap(u,v);vt=0;TQuery(id[v],id[u],tu);for(int i=1;i<=vt;i++) Adde(sts+V[i],stp+p);vt=0;TQuery(id[v],id[u],tv);for(int i=1;i<=vt;i++) Adde(stp+p,stt+V[i]);
}
inline void Solve(){int u,v;scanf("%d",&n);et=idt=0;for(int i=1;i<=n;i++) hd[i]=-1,sn[i]=0;for(int i=1;i<n;i++){scanf("%d%d",&u,&v);Adde(u,v),Adde(v,u);}Dfs1(1);Dfs2(1,1);scanf("%d",&m);et=0;stp=0,sts=m,stt=m+4*n,edp=m+8*n;for(int i=1;i<=edp;i++) hd[i]=-1,dg[i]=0;Build(1,1,n);for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);Modify(i,u,v);vt=0;Query(1,1,n,id[u],id[u]);for(int j=1;j<=vt;j++) Adde(stp+i,sts+V[j]);vt=0;Query(1,1,n,id[v],id[v]);for(int j=1;j<=vt;j++) Adde(stt+V[j],stp+i);}for(int i=1;i<=edp;i++)if(!dg[i]) S[++st]=i;while(st){u=S[st--];for(int i=hd[u];~i;i=e[i].nxt){v=e[i].v;dg[v]--;if(!dg[v]) S[++st]=v;}}for(int i=1;i<=edp;i++){if(dg[i]){puts("No");return;}}puts("Yes");
}
signed main(){int TT;scanf("%d",&TT);while(TT--) Solve();return 0;
}