关于冰茶姬
简述
冰茶姬是一种用于管理元素所属集合的数据结构,实现为一个森林,其中每棵树表示一个集合,树中的节点表示对应集合中的元素。
顾名思义,冰茶姬支持两种操作:
-
合并(Union):合并两个元素所属集合(合并对应的树)
-
查询(Find):查询某个元素所属集合(查询对应的树的根节点),这可以用于判断两个元素是否属于同一集合
冰茶姬在经过修改后可以支持单个元素的删除、移动;使用动态开点线段树还可以实现可持久化冰茶姬。
Code
Elaina's Code
int n,m;struct DSU{int fa[N];void init(){for(int i=1;i<=n;i++){fa[i]=i;//初始化自己的fa为自己}}int find(int x){//查询return x==fa[x]?x:fa[x]=find(fa[x]);//压缩路径//return x==fa[x]?x:find(fa[x]);//当然也可以不压缩}void unionn(int x,int y){//合并x=find(x),y=find(y);fa[y]=x;}bool check(int x,int y){//判断x=find(x),y=find(y);if(x==y) return 1;else return 0;}
}dsu;signed main(){n=rd,m=rd;while(m--){int op=rd,x=rd,y=rd;if(op==1){dsu.unionn(x,y);}else{if(dsu.check(x,y)) puts("Y");else puts("N");}}return Elaina;
}
启发式合并
过程
将节点较少或深度较小的树连到另一棵,以免发生退化。
Code
Elaina's Code
void unionn(int x,int y){x=find(x),y=find(y);if(x==y) return ;if(siz[x]<siz[y]) swap(x,y);fa[y]=x;siz[x]+=siz[y];
}//初始化
void init(){for(int i=1;i<=n;i++){fa[i]=i,siz[i]=1;}
}
带权冰茶姬
过程
开个数组 sum 记个和就完了。
直接看个例题吧。
例题
Almost Union-Find
题意
实现类似冰茶姬的数据结构,支持以下操作:
- 合并两个元素所属集合
- 移动单个元素
- 查询某个元素所属集合的大小及元素和
分析
操作1、3冰茶姬板子 乱糊就行
操作2嘛...他就挺有意思的...显然不能直接套冰茶姬。
举个例子,某次操作后如下图:
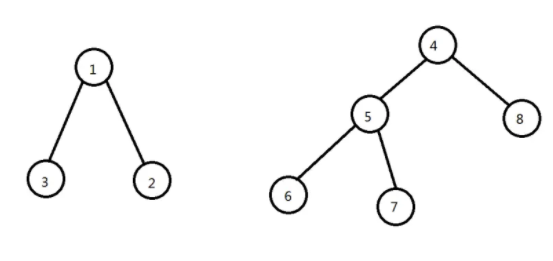
现要将 节点\(1\) 移动到 节点\(5\) 上,若正常套冰茶姬如下图
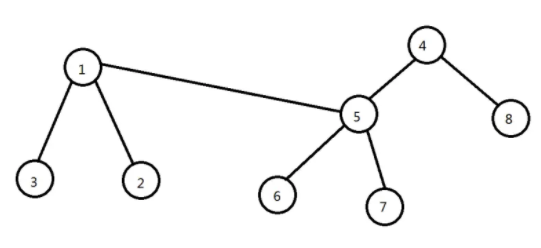
发现 节点\(3\) 和 节点\(2\) 也跟着一块飞过来了,会出现这种情况的原因是在第一个集合内,节点\(1\) 是这个集合内某一颗子树的根节点,也就是说,我们不想让这种情况发生,只能让所有的节点为这个集合/树的叶子节点,才能保证它们安然无恙的离开。
所以引入了一个概念:虚点。
具体操作是这样的:
我们可以对每个数 ii 建立虚点 i + ni+n 为它的上司。还是用上面那个栗子来理解:
然后建立虚点就会变成酱紫:
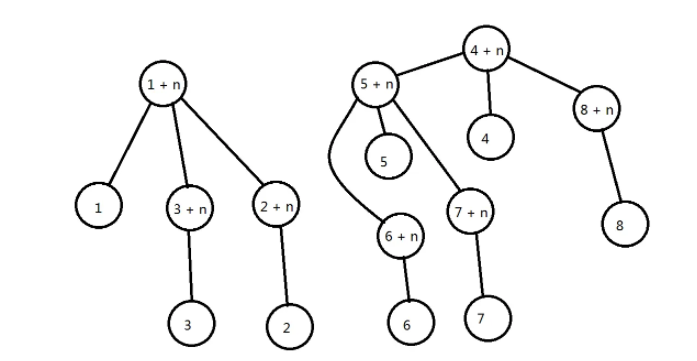
然后再进行上述操作就是酱紫
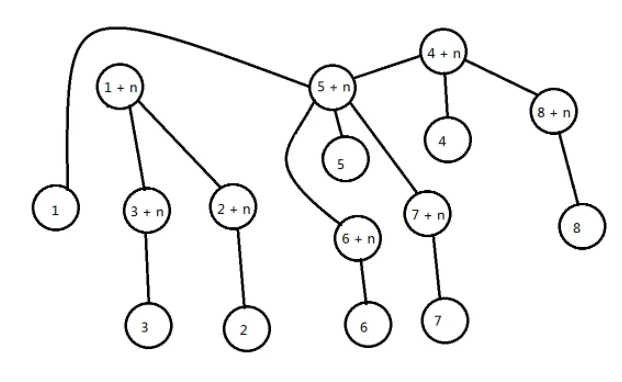
妙啊~ 很妙啊~
Code
Elaina's Code
int n,m;struct DSU{int fa[N<<1],sum[N],siz[N];void init(){for(int i=1;i<=n;i++){sum[i+n]=i;fa[i]=i+n;}for(int i=n+1;i<=n*2;i++){fa[i]=i,siz[i]=1;//xu dian}}int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}void unionn(int x,int y){x=find(x),y=find(y);if(x==y) return;if(siz[x]<siz[y]) swap(x,y);fa[y]=x;siz[x]+=siz[y],sum[x]+=sum[y];}void split(int x,int y){int fx=find(x),fy=find(y);if(fx==fy) return;--siz[fx],sum[fx]-=x;++siz[fy],sum[fy]+=x;fa[x]=fy;}
}dsu;signed main(){while(cin>>n>>m){dsu.init();while(m--){int op=rd,x,y;if(op==1){x=rd,y=rd;dsu.unionn(x,y);}else if(op==2){x=rd,y=rd;dsu.split(x,y);}else{x=rd;printf("%lld %lld\n",dsu.siz[dsu.find(x)],dsu.sum[dsu.find(x)]);}}}return Elaina;
}
可撤销冰茶姬
过程
用一个启发式合并的冰茶姬加上栈来存储合并信息即可.
Code
代码有猪食哦~
Elaina's Code
struct DSU{stack<int> sta;int fa[N],siz[N];void init(){for(int i=1;i<=n;i++){dis[i]=0,fa[i]=i,siz[i]=1;}}int find(int x){return x==fa[x]?x:find(fa[x]);//不可压缩路径,不然没法撤销了}void unionn(int x,int y){x=find(x),y=find(y);if(x==y) return ;if(siz[x]<siz[y]) swap(x,y);fa[y]=x;siz[x]+=siz[y];sta.push(y);//记录被合并的集合用于以后撤销}void undo(int x){//撤销while(sta.size()>x){//撤销到第x步操作int k=sta.top();sta.pop();siz[fa[k]]-=siz[k];//更新sizefa[k]=k;//分离}}
}dsu;
可持久化冰茶姬
扩展域冰茶姬
对于一个节点 \(i\) ,我们将其拆分为两个节点。一个属于集合 \(S\) ,另一个属于集合 \(T\) 。那么一条边所连接的两个节点就必须在不同的集合中。一个点在 \(S\) 中和在 \(T\) 的两个点属于一个集合,那么这张图就不是二分图。