题解：P10279 [USACO24OPEN] The Winning Gene S

思路

建议升蓝。

算法一

考虑暴力。

我们先枚举 \(K,L\)，考虑如何求解。

直接枚举每一个 \(K\)-mer，再枚举里面的每一个长度为 \(L\) 的子串，找到最大的子串并在起始部分打一个标记。最后直接看有几个地方被打标记就行。

时间复杂度：\(O(n^4)\)。预计能过测试点 \(1-4\)。

算法二

我们可以把选取子串的过程大概画下来。

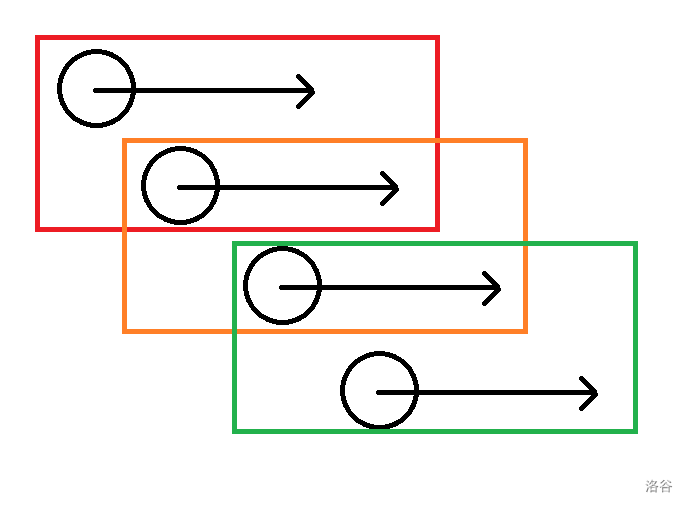
我们发现每一次都会往后面都会多一个子串，我们可以考虑一个数据结构，可以删除最前面的数据，而且可以往后面加入一个数据，并动态求最值。我在这里选择的数据结构为单调栈。

时间复杂度：\(O(n^3)\)，预计能过测试点 \(1-7\)。

代码

实践后：

（常数写大了，超了 0.07秒）

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
//#define int long long
namespace gtx{
//	Fast IOvoid read(int &x){x = 0;int h = 1;char tmp;do{tmp=getchar();if(tmp=='-')h*=-1;}while(!isdigit(tmp));while(isdigit(tmp)) x*=10,x+=tmp-'0',tmp=getchar();x*=h;}void read(char &x){do{x=getchar();}while(x==' '||x=='\n'||x=='\r');}void write(char x){putchar(x);}void write(int x){if(x<0) putchar('-'),x=-x;int st[200]={0},tot=0;do{st[++tot]=x%10,x/=10;} while(x);while(tot){putchar(st[tot--]+'0');};}void write(int x,char y){write(x);write(y);}const int MAXN = 3100;int n,ans,t[MAXN];char a[MAXN];signed main(){read(n);for(int i = 1;i<=n;i++) read(a[i]);for(int K = 1;K<=n;K++){for(int L = 1;L<=K;L++){deque<pair<int,string>> st;string now;for(int i = 1;i<=L;i++) now += a[i];st.push_back({1,now});for(int i = 2;i<=K-L+1;i++){now.erase(now.begin());now += a[i+L-1];while(!st.empty()&&st.back().second>now) st.pop_back();st.push_back({i,now});}bitset<MAXN> b;b.set(st.front().first);for(int i = K-L+2;i<=n-L+1;i++){if(st.front().first==i-(K-L)-1) st.pop_front();now.erase(now.begin());now += a[i+L-1];while(!st.empty()&&st.back().second>now) st.pop_back();st.push_back({i,now});b.set(st.front().first);}t[b.count()]++; }}for(int i = 1;i<=n;i++) write(t[i],'\n');return 0;}
}
signed main(){
//	freopen("gene.in","r",stdin);
//	freopen("gene.ans","w",stdout);
//	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T = 1;
//	gtx::read(T);while(T--) gtx::main();return 0;
}

算法三

我们在上面的代码中发现其实 \(K\) 有没有都几乎没有什么区别，于是可以想一想定长的 \(L\) 可以对哪些答案产生的贡献。

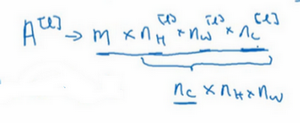
记录前面第一个比这个子串大的子串的起始位置为 \(left_i\)，后面第一个比这个子串大的子串的起始位置为 \(right_i\)。那么对于一个子串来说，如果这个子串能产生贡献 \(K\) 最大应该的值的区间应该是这样的：

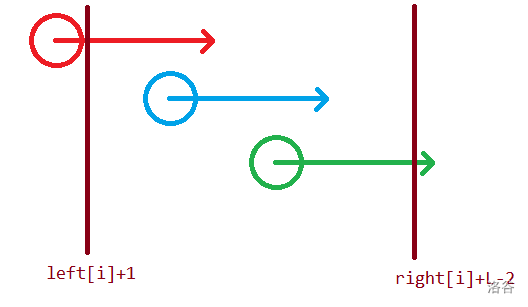
所以产生的最大的 \(K\) 为 \(right_i+L-2-left_i\)。最小的 \(K\) 应该就是这个子串的长度，那么这个子串就会对这些 \(K\) 产生答案。我们可以用差分解决。

时间复杂度：\(O(n^2)\)。预计得分：\(100pts\)。

AC代码

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
//#define int long long
namespace gtx{
//	Fast IOvoid read(int &x){x = 0;int h = 1;char tmp;do{tmp=getchar();if(tmp=='-')h*=-1;}while(!isdigit(tmp));while(isdigit(tmp)) x*=10,x+=tmp-'0',tmp=getchar();x*=h;}void read(char &x){do{x=getchar();}while(x==' '||x=='\n'||x=='\r');}void write(char x){putchar(x);}void write(int x){if(x<0) putchar('-'),x=-x;int st[200]={0},tot=0;do{st[++tot]=x%10,x/=10;} while(x);while(tot){putchar(st[tot--]+'0');};}void write(int x,char y){write(x);write(y);}const int MAXN = 3100;int n,t[MAXN],ans[MAXN][MAXN],left[MAXN],right[MAXN];char a[MAXN];signed main(){read(n);for(int i = 1;i<=n;i++) read(a[i]);for(int L = 1;L<=n;L++){stack<pair<int,string>> st;string now;for(int i = 1;i<=L;i++) now += a[i];st.push({1,now});for(int i = 1;i<=n-L+1;i++) left[i] = 0;for(int i = 1;i<=n-L+1;i++) right[i] = 0;left[1] = 1;for(int i = 2;i<=n-L+1;i++){now.erase(now.begin());now += a[i+L-1];while(!st.empty()&&st.top().second>now) st.pop();left[i] = st.empty()?1:st.top().first+1;st.push({i,now});}while(!st.empty()) st.pop();now="";for(int i = n-L+1;i<=n;i++) now+=a[i];right[n-L+1] = n;st.push({n-L+1,now});for(int i = n-L;i>=1;i--){now.erase(--now.end());now = a[i]+now;while(!st.empty()&&st.top().second>=now) st.pop();right[i] = st.empty()?n:st.top().first+L-2;st.push({i,now});}for(int i = 1;i<=n-L+1;i++){if(right[i]-left[i]+1<L) continue;ans[L][L]++;ans[right[i]-left[i]+2][L]--;}
//				cout << L << endl;
//				for(int i = 1;i<=n;i++) cout << left[i] << " " << right[i] << endl;}for(int j = 1;j<=n;j++){for(int i = j;i<=n;i++){ans[i][j] += ans[i-1][j];t[ans[i][j]]++;}}for(int i = 1;i<=n;i++) write(t[i],'\n');return 0;}
}
signed main(){
//	freopen("gene.in","r",stdin);
//	freopen("gene.out","w",stdout);
//	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T = 1;
//	gtx::read(T);while(T--) gtx::main();return 0;
}