CF 2001 E2
由于对称,所以设 \(heap[u]\) 为两次确定堆,且第一次弹出的是 \(u\),\(heap[u,v]\) 是第一次 \(u\) ,第二次 \(v\)
则答案就是 \(\sum heap[u]=2^{n-1}·heap[x]\)
其中 \(x\) 任意。
不妨我们考虑第一次都是从第一个叶子弹出,那么对于其他不同的第二个弹出的点,根据对称性显然有如下性质:
\(LCA(u,v_1)=LCA(u,v_2)\implies heap[u,v_1]=heap[u,v_2]\)
而经过手玩一下关系,可以发现:
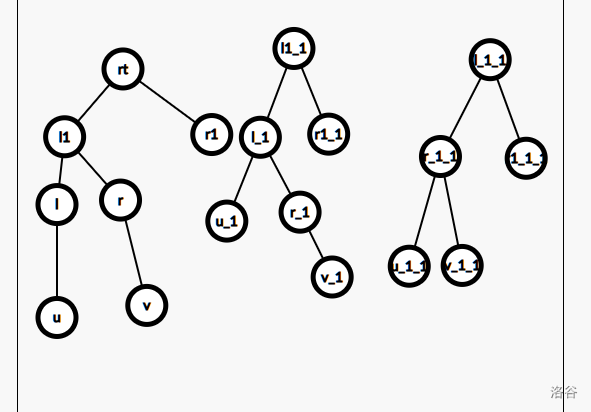
也就是设 \(L_1,R_1\) 是两个叶子的 \(LCA\) 的左右儿子,\(l,r\) 是 \(L_1\) 的左右儿子(图稍微画错了点)
容易得到:
而对于更上层的点,还是设当前点左右儿子是 \(L_1,R_1\),\(L_1\) 的儿子是 \(l,r\),则有:
由 E1,我们求出了 \(f_{i,j}\):高为 \(i\) 的堆,操作 \(j\) 次,只弹出第一个叶子的方案数,以及 \(g_{i,j}\):操作 \(j\) 次的总局面个数
借用一张官解的图
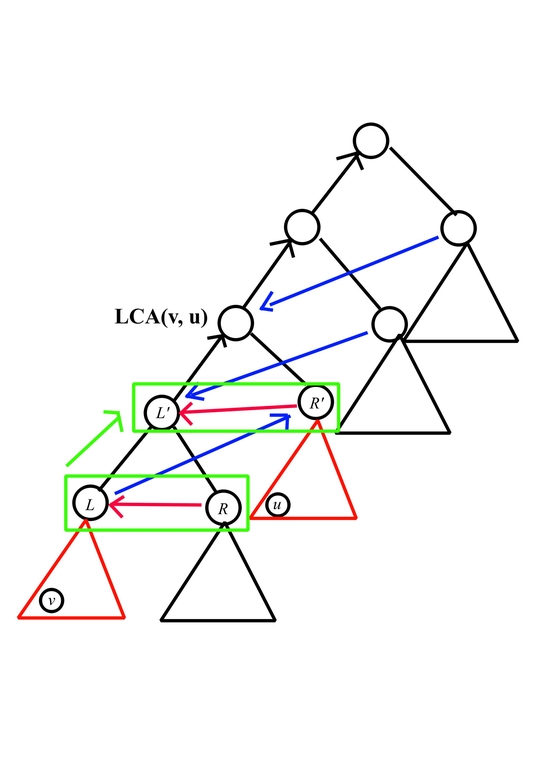
我们会发现 \(L,R\to L'\) 的时候,\(R\) 是普通子树,而 \(R'\) 是一颗满足弹一次合法的子树。
所以 \(L'\) 的方案数可以由符合条件的 \(L,R\),\(f_{L}·g_R\) 构成,而总的方案数需要再用 \(f_{R'}\) 进行合并。
而用 \(f_{R'}\) 合并的时候要乘上 \(2^{h-2}\) 因为叶子任选其一。
而也有可能自身不是 \(LCA\),往上更新的时候直接算就行了,注意要拼上一个普通二叉堆个数。
所以可以设 \(dp_{h,l,r}\) 为高为 \(h\) 的树,左子树权值 \(l\),右子树权值为 \(r\) 的方案数。
那么有:
可以利用前缀和优化到 \(O(nk^2)\),例如前半部分,可以设 \(S_{x,y}=\sum_{l,r}f_{h-2,l}·g_{h-2,r}·[l+r=x][l=y][l>r]\),先做 \(y\) 这一维的前缀和,再做 \(x\) 这一维的前缀和即可。
后半部分同理。
code