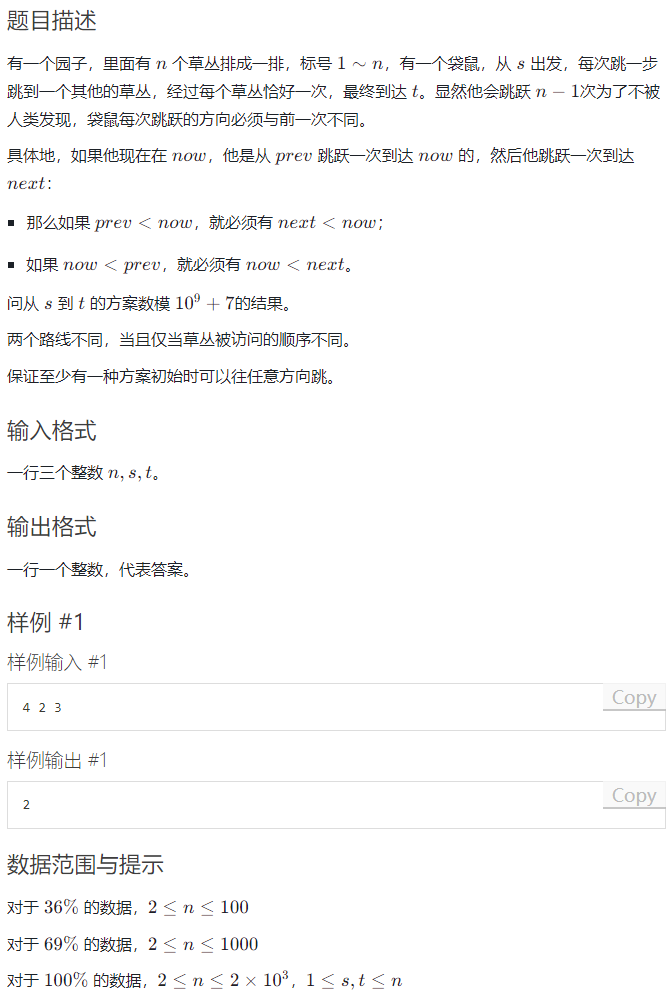
先转化一下题意:求有多少个1~n的排列p能够满足 \(\forall i \in (1,n)\) ,使 $ p_{i} $ 左右两边的数同时小于或者大于 \(p_{i}\) ,并且\(p_{1}=s,p_{n}=t\) 。
比较明显的预设型DP(连转化题意我都做不到,悲),先正常来分析一下,我们填数从小往大枚举,如果我们填入一个数,它无非就两种可能,一种是开拓出一个新的区间,或者是把两个区间合并到一起,不可能填在边界而不合并区间,因为如果这样,我们填的这个数它旁边有一个小于它的数,未来还要再在它旁边填数,这个数一定大于它,无法满足左右两边的数同时大于它或小于它的条件。
根据上面的分析,我们不妨设 \(dp[i][j]\) 表示目前填到第 \(i\) 个数,目前有 \(j\) 个连续的区间。
那来列状态转移方程,首先如果是合并区间,那它有 \(j+1-1\) 个地方可以放数. \(dp[i][j]=dp[i-1][j+1]*j\)
如果是拓展出新的区间,那它也是有 \(j-1+1\) 个可以填数的地方. \(dp[i][j]=dp[i-1][j-1]*j\)
那到这里就有一个问题,咱们把 \(p_{1}=s,p_{n}=t\) 这个条件给丢了。
那我们接着分析,先考虑加上这个条件对我们刚才的转移会有什么影响,很明显当我们填上 \(s\) 和 \(t\) 时,相当于整个区间的最左边界和最右边界已经确定,不会在改变,我们就无法再进行拓展,于是我们更改一下状态转移方程 \(dp[i][j]=dp[i-1][j-1]*(j-(i>s)-(i>t))\)
那我们接着考虑如果填的数为 \(s,t\) 时,我们怎么做,它同样可以拓展出一个新的区间,它还可以接在最左或最右边区间上,因为它的拓展位置是固定的,我们给它乘 \(1\) 就行。 \(dp[i][j]=dp[i-1][j-1]+dp[i-1][j]\)
到这里这道题就算是结束了。
using namespace std;#define int long long
const int N=2e3+107;
const int mod=1e9+7;int n,s,t;int dp[N][N];int read()
{int f=1,s=0;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){s=(s<<1)+(s<<3)+(ch^48);ch=getchar();}return f*s;
}signed main()
{freopen("kang.in","r",stdin);freopen("kang.out","w",stdout);n=read(),s=read(),t=read();dp[1][1]=1;for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){if(i!=s&&i!=t) dp[i][j]=(j*dp[i-1][j+1]%mod+(j-(i>s)-(i>t))*dp[i-1][j-1]%mod)%mod;else dp[i][j]=dp[i-1][j-1]+dp[i-1][j];}}printf("%lld",dp[n][1]);
}`