线段树（2）——懒惰标记Lazy Tag（单运算）及例题

上一篇文章我们讲了线段树的最基本的操作。如果有一种操作叫做区间加法呢？这个时候显然可以依次单点修改，但是时间复杂度太高了。所以可以考虑优化，由于思考过程可能很长，此处直接引入懒惰标记。

懒惰标记就是在对一颗树的所有节点进行某种统一操作时，只对根节点做一个标记表示它的子树都要进行这个操作，但是懒惰标记仅可用于能够计算出若对树上的每个节点进行操作时，能够通过根节点直接算出查询值。这可能有些复杂，举个例子，上次的题目有一道需要区间开方根，查询的是和，对一个树开方根然后求和，这是和其子树上每一个点的值有关的，因此不能使用懒惰标记。而区间加减，只需要通过树的和加上操作数乘以子树大小即可。区间乘法，区间赋值都是可以的。

讲了这么多没用的，看看懒惰标记是怎么实现的吧。比如给区间 \([2,5]\) 同时加上 \(x\)，那么假设数组总共有 \(5\) 个元素，那么线段树如下（其实就是不停的用同一个而以惹）：

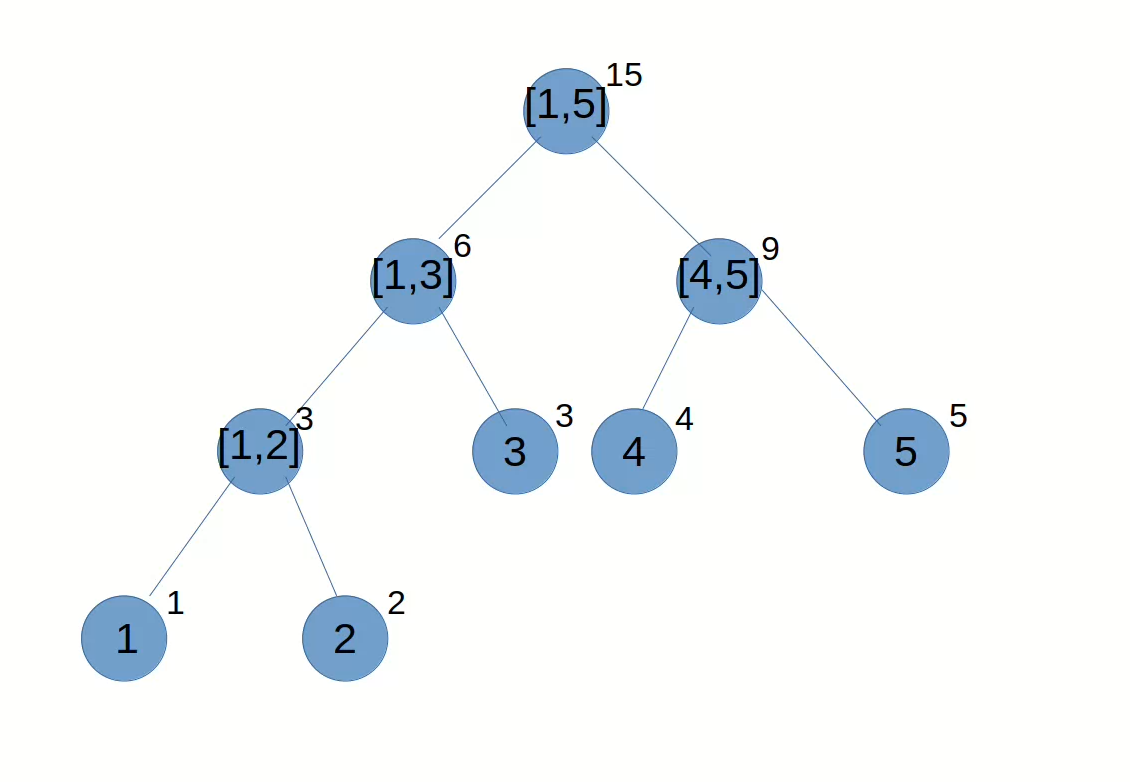
那么到 \([4,5]\) 的时候，很显然是完全包含的，所以给 \([4,5]\) 的懒惰标记 加上 \(x\)，因为懒惰标记是有可能叠加的。左边的分别是到叶子节点 \(2\) 和 \(3\)，这个时候应该如何处理呢？其实是不用特判叶子的，因为叶子即使用懒惰标记，也不会影响，这个懒惰标记存在是合理的，如果不存在，也不会影响。那么现在要访问 \([4,4]\) 的和，遍历中会遇到有懒惰标记的节点的子结点，这个时候如果还保持懒惰标记不变显然就没有什么意义了，而且访问到 \(4\) 的值是区间增加前的。所以当需要访问有懒惰标记的结点的子结点的信息时，需要使用下放操作。下放操作即将懒惰标记的信息发放到子结点，由于懒惰标记保存的是 \(x\) 而不是 \(x \times (tr-tl+1)\)，所以只需要将左右子结点的懒惰标记加上 \(lazy_now\)，线段树的值加上：左子结点加上 \(lazy_now \times (mid-tl+1)\)；右子结点加上 \(lazy_now \times (tr-mid)\)。然后清空 \(lazy_now\)。代码如下，设下放操作为函数 \(push_down\)：

void push_down(int now,int tl,int tr){int mid=(tl+tr)/2;t[now*2]+=lazy[now]*(mid-tl+1);t[now*2+1]+=lazy[now]*(tr-mid);lazy[now*2]+=lazy[now];lazy[now*2+1]+=lazy[now];lazy[now]=0;
}

在修改和查询操作的时候，需要在判断区间在需要操作的区间完全包括内或完全不包括内之后即不完全包括时，需要加入下放操作即：

if(tl>=l&&tr<=r){...
}
if(tl>r||tr<l){...
}
push_down(now,tl,tr);

完整代码为：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,a[N],t[N*4],lazy[N*4];
//push_down：下放操作
void push_down(int now,int tl,int tr){int mid=(tl+tr)/2;t[now*2]+=lazy[now]*(mid-tl+1);t[now*2+1]+=lazy[now]*(tr-mid);lazy[now*2]+=lazy[now];lazy[now*2+1]+=lazy[now];lazy[now]=0;
}
//build：建树
void build(int now,int tl,int tr){if(tl==tr){t[now]=a[tl];return ;}int mid=(tl+tr)/2;build(now*2,tl,mid);build(now*2+1,mid+1,tr);t[now]=t[now*2]+t[now*2+1];
}
//add：now表示当前结点，tl和tr表示线段树的区间，l和r表示需要增加数值的区间，x表示增加的值
void add(int now,int tl,int tr,int l,int r,int x){if(tl>=l&&tr<=r){t[now]+=x*(tr-tl+1);lazy[now]+=x;return ;}if(tl>r||tr<l){return ;}if(lazy[now]){push_down(now,tl,tr);}int mid=(tl+tr)/2;add(now*2,tl,mid,l,r,x);add(now*2+1,mid+1,tr,l,r,x);t[now]=t[now*2]+t[now*2+1];
}
//query：查询
int query(int now,int tl,int tr,int l,int r){if(tl>=l&&tr<=r){return t[now];}if(tl>r||tr<l){return 0;}if(lazy[now]){push_down(now,tl,tr);}int mid=(tl+tr)/2;return query(now*2,tl,mid,l,r)+query(now*2,mid+1,tr,l,r);
}
int main(){n=5;a[1]=1,a[2]=2,a[3]=3,a[4]=4,a[5]=5;build(1,1,n);add(1,1,n,2,4,5);cout<<query(1,1,n,1,5);return 0;
}

区间乘法也可以仿制。注意，build的时候需要设置懒惰标记为 \(1\)。假设这里求区间和。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,a[N],t[N*4],multi[N*4];
void push_down(int now,int tl,int tr){int mid=(tl+tr)/2;t[now*2]+=multi[now]*(mid-tl+1);t[now*2+1]+=multi[now]*(tr-mid);multi[now*2]*=multi[now];multi[now*2+1]*=multi[now];multi[now]=1;
}
void build(int now,int tl,int tr){multi[now]=1;if(tl==tr){t[now]=a[tl];return ;}int mid=(tl+tr)/2;build(now*2,tl,mid);build(now*2+1,mid+1,tr);t[now]=t[now*2]+t[now*2+1];
}
void mul(int now,int tl,int tr,int l,int r,int x){if(tl>=l&&tr<=r){t[now]*=x;multi[now]+=x;return ;}if(tl>r||tr<l){return ;}if(multi[now]!=1){push_down(now,tl,tr);}int mid=(tl+tr)/2;mul(now*2,tl,mid,l,r,x);mul(now*2+1,mid+1,tr,l,r,x);t[now]=t[now*2]+t[now*2+1];
}
int query(int now,int tl,int tr,int l,int r){if(tl>=l&&tr<=r){return t[now];}if(tl>r||tr<l){return 0;}if(multi[now]!=1){push_down(now,tl,tr);}int mid=(tl+tr)/2;return query(now*2,tl,mid,l,r)+query(now*2+1,mid+1,tr,l,r);
}
int main(){n=5;a[1]=1,a[2]=2,a[3]=3,a[4]=4,a[5]=5;build(1,1,n);mul(1,1,n,2,4,5);cout<<query(1,1,n,1,5)<<" "<<query(1,1,n,4,4);return 0;
}

在做懒惰标记这类题目时，重点在于多思考，最好画个图模拟一下，看看每个地方是怎么改的，怎么下放的，思想很重要，代码也重要。线段树好写好调，对着模板多写几遍，就不容易出错了，一般在写大型题目时，建议先写线段树，然后弄几个简单的例子测一下线段树有没有写错再下一步写。

区间乘法，查询区间积；区间加法，查询区间积等都建议自己思考思考。一般来说CSP-J中线段树的题目真正应用的时候不会出的太难，所以仅仅是不会线段树想了解了解或者不打CSP-S的人可以止步这里了，接下来线段树（3）的内容要开始烧脑了。

例题

【模板】线段树 1

模板题。貌似要开long long。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10;
ll n,m,a[N],t[N*4],lazy[N*4];
void build(ll now,ll tl,ll tr){if(tl==tr){t[now]=a[tl];return ;}ll mid=(tl+tr)/2;build(now*2,tl,mid);build(now*2+1,mid+1,tr);t[now]=t[now*2]+t[now*2+1];
}
void push_down(ll now,ll tl,ll tr){ll mid=(tl+tr)/2;t[now*2]+=lazy[now]*(mid-tl+1);t[now*2+1]+=lazy[now]*(tr-mid);lazy[now*2]+=lazy[now];lazy[now*2+1]+=lazy[now];lazy[now]=0;
}
ll query(ll now,ll tl,ll tr,ll l,ll r){if(tl>=l&&tr<=r){return t[now];}if(tl>r||tr<l){return 0;}if(lazy[now]){push_down(now,tl,tr);}ll mid=(tl+tr)/2;return query(now*2,tl,mid,l,r)+query(now*2+1,mid+1,tr,l,r);
}
void add(ll now,ll tl,ll tr,ll l,ll r,ll x){if(tl>=l&&tr<=r){lazy[now]+=x;t[now]+=x*(tr-tl+1);return ;}if(tl>r||tr<l){return ;}if(lazy[now]){push_down(now,tl,tr);}ll mid=(tl+tr)/2;add(now*2,tl,mid,l,r,x);add(now*2+1,mid+1,tr,l,r,x);t[now]=t[now*2]+t[now*2+1];
}
int main(){//freopen("xx.in","r",stdin);//freopen("xx.out","w",stdout);ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;for(ll i=1;i<=n;i++){cin>>a[i];}build(1,1,n);for(ll i=1;i<=m;i++){ll opt,x,y,k;cin>>opt>>x>>y;if(opt==1){cin>>k;add(1,1,n,x,y,k);}else{cout<<query(1,1,n,x,y)<<"\n";}}return 0;
}

自行查找。由于线段树的题大多数是多个标记的，所以题目不多。