相遇（容斥+最短路+分类，水紫）

第5题     相遇 查看测评数据信息

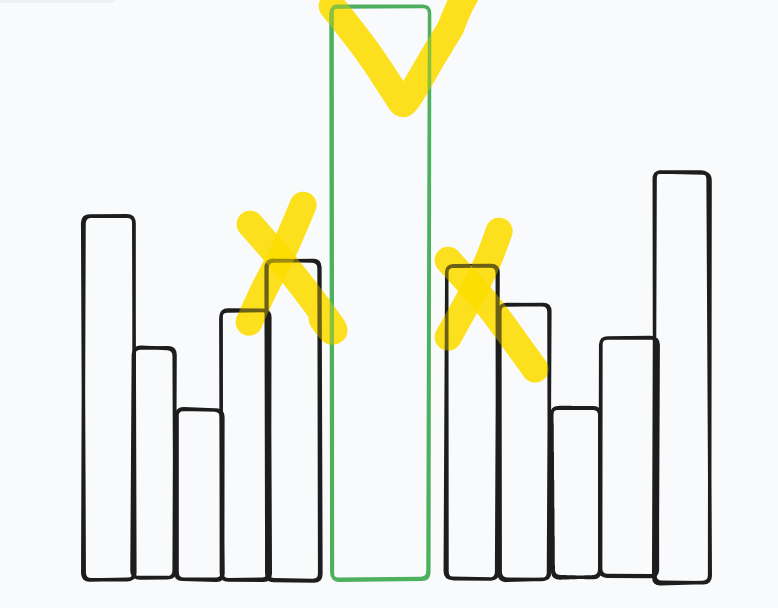
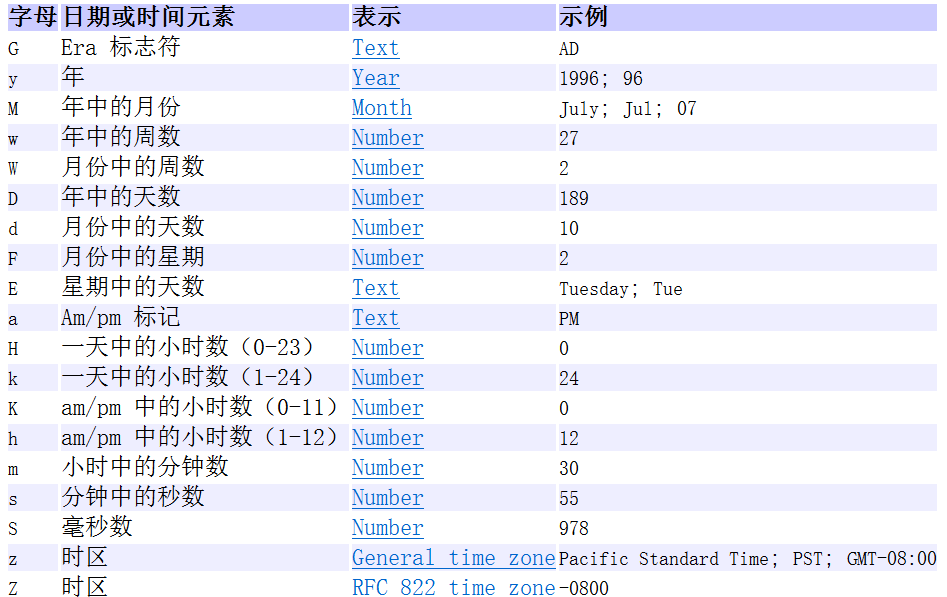
给定一个有n个节点m条边的无向图，在某一时刻节点st上有一个动点a, 节点end上有一个动点b, 动点a向节点end方向移动，要求是尽快到达end点，与此同时，动点b向节点st方向移动，要求是尽快到达st点， 但是整个过程中a和b不能相遇，问两点不相遇一共有多少种方案。

不相遇是指在同一时刻两点都不在同一节点或同一边上。结果可能很大，对1e9+7取模

输入格式

 

第一行两个整数n和m

第二行两个整数st和end

接下来m行，每行三个整数u,v,t， 表示u和v有一条长为t的边

其中1<=n<=1e5, 1<=m<=2e5,1<=t<=1e9

数据不存在重边和自环

 

输出格式

 

一个整数

 

输入/输出例子1

输入：

4 4

1 3

1 2 1

2 3 1

3 4 1

4 1 1

 

输出：

2

 

样例解释

无

 

直接求不相遇比较难，用减法原理。

很容易想到，首先要搞一个最短路计数。

dis[i]:s->i最短路，cnt[i]：s->i的最短路路径数
dis2[i]:t->i最短路，cnt2[i]：t->i的最短路路径数

 

用全部方案-相遇方案，就是答案

全部方案：最短路径条数平方。也就是 cnt[t]*cnt[t]（cnt2[s]*cnt2[s] 也行）

相遇是在节点上相遇或者边上相遇

分别算就好

 

判断能否在u节点相遇：

枚举每个点，看看能否在点上相遇

条件：看看dis[s->u]是否等于dis[t->u]，且s-u + t-u 是最短路

贡献：(cnt[u]*cnt2[u])^2

计算如下：

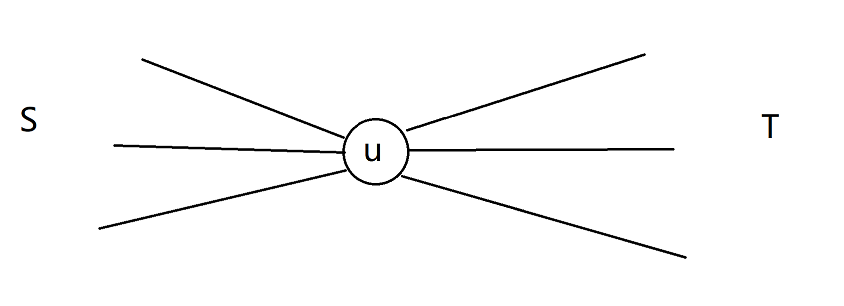
假设s到u有3条路可以走，t到u也有3条路可以走

那么我们可以考虑让s走第1条，走到t可以分别走3条。

我们还可以考虑让s走第2条，走到t可以分别走3条。

我们还可以考虑让s走第3条，走到t可以分别走3条。

所以就是 cnt[u]*cnt2[u]

但是我们还可以反过来，从t走，走到s

那么我们可以考虑让t走第1条，走到s可以分别走3条。

我们还可以考虑让t走第2条，走到s可以分别走3条。

我们还可以考虑让t走第3条，走到s可以分别走3条。

所以就是 cnt[u]*cnt2[u]

那么答案就是这俩相乘。

 

 

 

边上相遇：

枚举每条边，是否会在那条边相遇。

条件：这条边在最短路上。  s-u+w+t-v 是最短路

还有两个条件：

 

 

 

贡献：(cnt[s-u]*cnt[t-v])^2

和计算点的贡献是一样的。