平面几何基本功：用导角法解决若干问题

引理1 如图, 设锐角\(\small \triangle ABC\)的外接圆为\(\small\Omega, X,Y,Z\)分别是劣弧\(\small\mathop{BC}\limits^\frown,\mathop{AC}\limits^\frown,\mathop{AB}\limits^\frown\)的中点.证明：\(\small\triangle XYZ\)的垂心是\(\small\triangle ABC\)的内心.

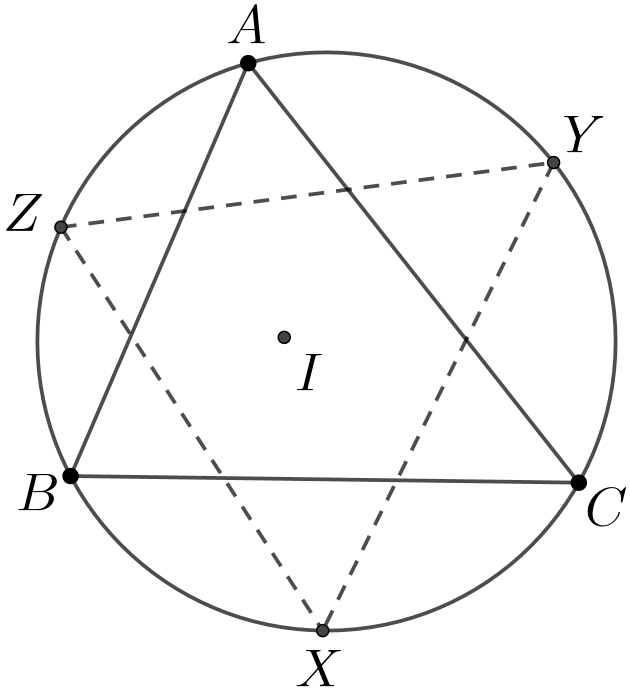
分析：易知\(\small AX,BY,CZ\)是角平分线, 所以只需证明\(\small \triangle ABC\)的内心\(\small I\)就是\(\small \triangle XYZ\)的垂心. 换言之, 即证明\(\small AX\perp YZ,BY\perp XZ,CZ\perp XY\), 于是可以将垂直关系转化为两角和等于90\(^\circ\), 接下来利用导角法完成即可.

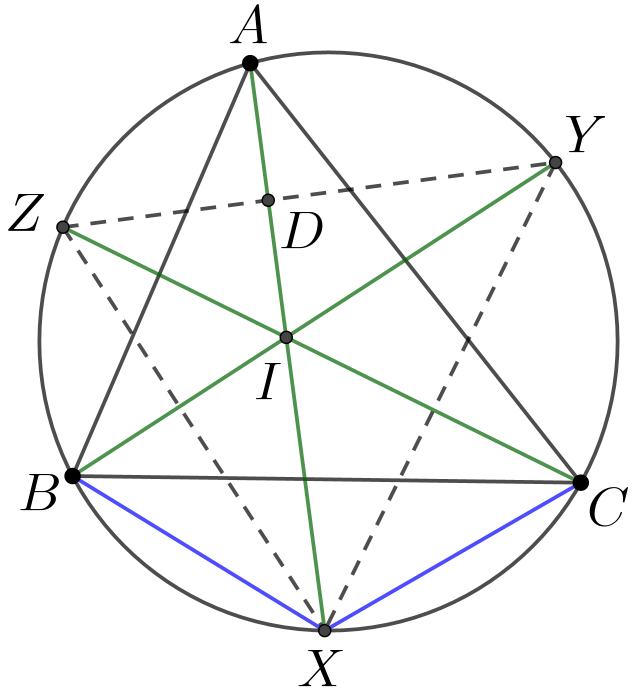
证：因为\(\small \angle XZY=\angle XBY=\angle XBC+\angle CBY=\angle XAC+\angle CBY\),所以我们有,

\[\small \begin{align*}\angle XZY+\angle AXZ&=\angle XAC+\angle CBY+\angle AXZ\\&=\angle XAC+\angle CBY+\angle ACZ\\&=\frac{1}{2}(\angle BAC+\angle CBA+\angle ACB)\\&=90^\circ, \end{align*} \]

这说明\(\small AX\perp YZ\),同理可得\(\small BY\perp XZ,CZ\perp XY\).所以, \(\small \triangle ABC\)的内心\(I\)就是\(\small \triangle XYZ\)的垂心.

问题1(JMO2011/5) 点\(\small A,B,C,D,E\)在圆\(\small \omega\)上, 而点\(\small P\)在圆\(\small \omega\)外.这些点满足：(1)直线\(\small PB,PD\)与圆\(\small \omega\)相切;(2)\(\small P,A,C\)共线;(3)\(\small \overline{DE}\parallel \overline{AC}\).证明：\(\small \overline{BE}\) 平分\(\small \overline{AC}\).

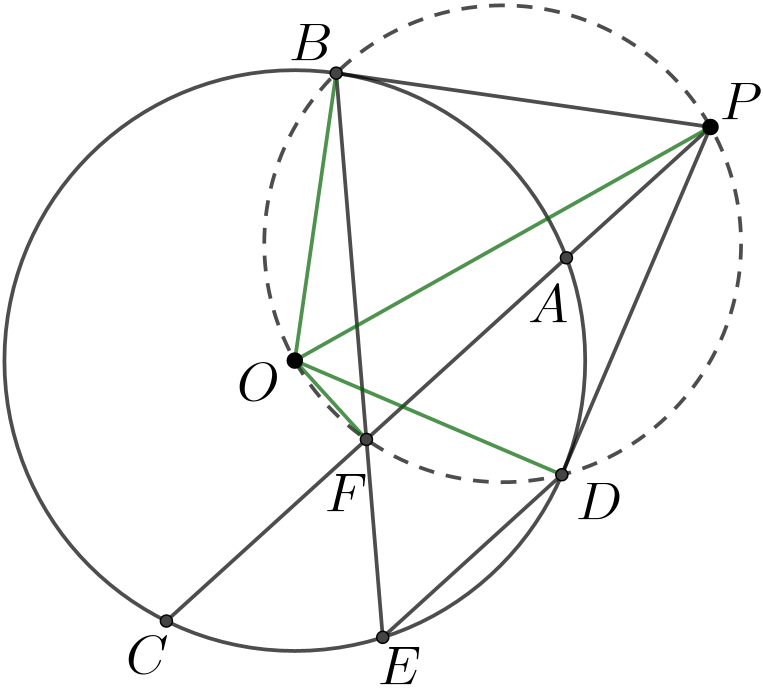
分析：\(\small OF\perp AC\)等价于\(\small F\)为\(\small AC\)中点, 将线段数量关系转化为位置关系是解题关键.

证：
根据题目条件(3)知\(\small \angle BFP=\angle BED\),又因为\(\small \angle BED=\frac{1}{2}\angle BOD=\angle BOP\),所以\(\small \angle BFP=\angle BOP\),这说明\(\small B,O,F,P\)四点共圆.于是我们有,

\[\small\angle FOP+\angle OPF=\angle FBP+\angle OBF=90^\circ, \]

即\(\small OF\perp AC\),所以\(\small F\)为\(\small AC\)中点.

引理2 如图,设锐角\(\small \triangle ABC\)中, \(\small \overline{BE},\overline{CF}\)是高, \(\small M\)是\(\small \overline{BC}\)的中点.证明:\(\small \overline{ME},\overline{MF}\)和过\(\small A\)与\(\small \overline{BC}\)平行的直线均与圆\(\small (AEF)\)相切.

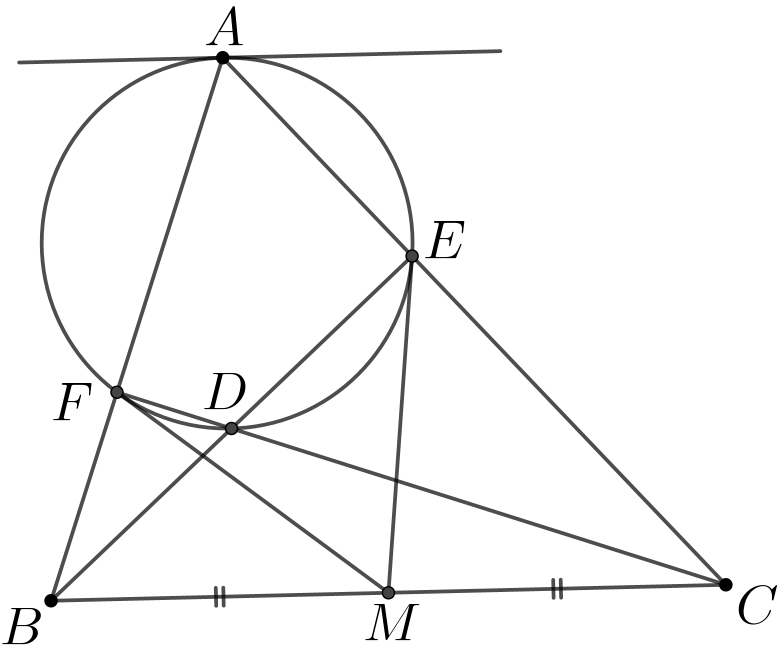
证：设\(\small \overline{BE}\)与\(\small \overline{CF}\)交于点\(\small D\).因为\(\small \angle DFA=\angle DEA=90^\circ\), 所以\(\small A,F,D,E\)四点共圆, 且\(\small \overline{AD}\)为直径, 由题意知\(\small D\)为\(\small \triangle ABC\)垂心, 这说明\(\small \overline{AD}\perp \overline{BC}\), 所以过\(\small A\)与\(\small \overline{BC}\)平行的直线垂直于\(\small \overline{AD}\), 所以该直线与圆\(\small (AEF)\)相切. 接下来证明\(\small \overline{MF}\)与\(\small \overline{OF}\)垂直.

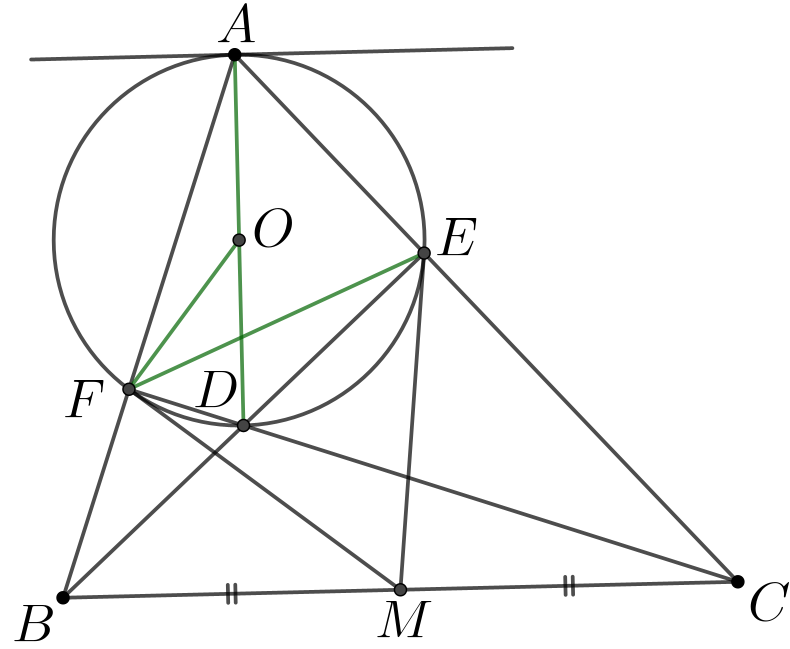
首先注意到\(\small E,F,B,C\)四点共圆且\(\small M\)是\(\small \overline{BC}\)中点, 那么\(\small \overline{MF}=\overline{MC}\), \(\small \angle BCF=\angle BEF=\angle DAF\). 所以,

\[\small \angle MFO=\angle MFC+\angle DFO=\angle DAF+\angle ODF=90^\circ. \]

这说明\(\small \overline{MF}\)与\(\small \overline{OF}\)垂直, 即\(\small \overline{MF}\)与圆\(\small (AEF)\)相切. 同理可得, \(\small \overline{ME}\)与圆\(\small (AEF)\)相切.

引理3(内切圆弦上的直角) 如图, 设\(\small \triangle ABC\)的内切圆在边\(\small \overline{BC},\overline{AC},\overline{AB}\)上的切点分别是\(\small D,E,F\), 内切圆圆心为\(\small I\). 设\(\small M,N\)分别是$\overline{BC},\overline{AC} \(的中点.射线\)\small BI\(与直线\)\small EF\(相交于\)\small K\(. 证明：\)\small \overline{BK}\perp \overline{CK}\(, 并且\)\small K\(在直线\)\small MN$上.

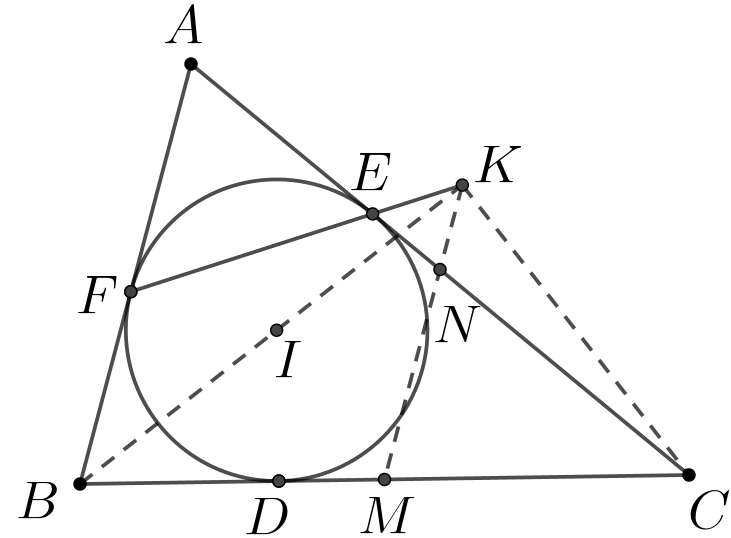
分析：不妨将结论换一种方向, 假设射线\(\small BI\)与直线\(\small MN\)相交于\(\small K'\), 然后证明\(\small K'\)在直线\(\small EF\)上.

证： 假设射线\(\small BI\)与直线\(\small MN\)相交于\(\small K'\). 因为\(\small MN\parallel AB\),所以\(\small \angle BK'M=\angle ABK'=\angle K'BM\), 这说明\(\small \triangle BMK'\)是等腰三角形, 即有\(\small K'M=BM\), 又因为\(\small BM=CM\), 所以\(\small \angle BK'C=90^\circ\), 即\(\small \overline{BK}\perp \overline{CK}\). 下面证明\(\small K'\)在直线\(\small EF\)上.

\[\small \begin{align*}\overline{EN}&=\frac{1}{2}\overline{AC}-\overline{AE}\\\overline{NK}&=\overline{MK}-\overline{MN}=\frac{1}{2}\overline{BC}-\overline{AB}\\\overline{EN}-\overline{NK}&=\frac{1}{2}\overline{AC}-\overline{AE}+\frac{1}{2}(\overline{AB}-\overline{BC})\\&=\frac{1}{2}\overline{AC}-\overline{AE}+\frac{1}{2}(\overline{AE}-\overline{CE})\\&=\frac{1}{2}\overline{AC}-\frac{1}{2}\overline{AE}-\frac{1}{2}\overline{CE}\\&=\frac{1}{2}\overline{AC}-\frac{1}{2}\overline{AC}=0^\circ, \end{align*} \]

于是\(\small \overline{EN}=\overline{NK}\), 又因为\(\small \angle ENK'=\angle MNC=\angle A\), 所以\(\small \triangle NEK'\sim \triangle AEF\),可得\(\small \angle NEK'=\angle AEF\), 注意到\(\small A,E,N\)共线, 故\(\small E,F,K'\)共线, 这说明射线\(\small BI\)与直线\(\small EF\)交于点\(\small K'\), 所以\(\small K'\)与\(\small K\)为同一点.

问题2(加拿大1997/4) 点\(\small O\)在平行四边形\(\small ABCD\)内部, 使得\(\small \angle AOB+\angle COD=180^\circ\).证明：\(\small \angle OBC=\angle ODC\).

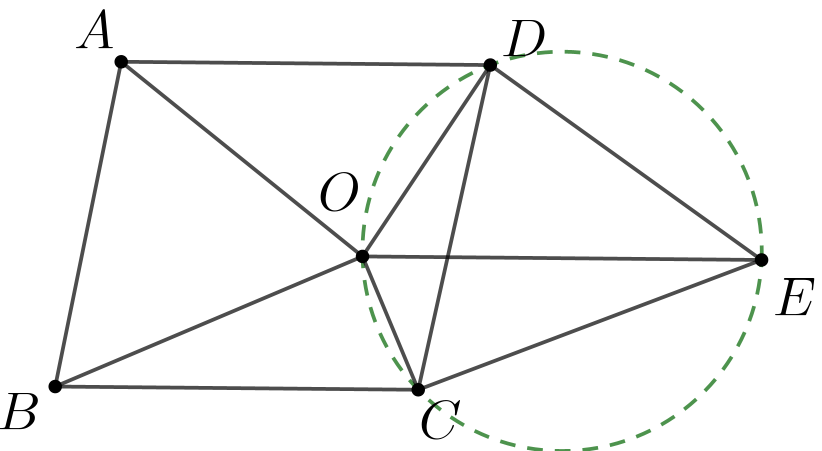
证： 将\(\small \triangle ABO\)平移至\(\small \triangle DCE\),\(\small \angle COD+\angle DEC=\angle COD+\angle AOB=180^\circ\),所以\(\small O,D,E,C\)四点共圆, 易得\(\small \angle ODC=\angle OEC\).因为\(\small \triangle BOC\simeq \triangle ECO\), 所以\(\small \angle OBC=\angle OEC=\angle ODC\).

问题3(IMO2006/1) 设\(\small \triangle ABC\)的内心为\(\small I,P\)在三角形内部, 满足
$$\small \angle PBA+ \angle PCA=\angle PBC+\angle PCB.$$
证明：\(\small AP\ge AI\),等号成立当且仅当\(\small P=I\).

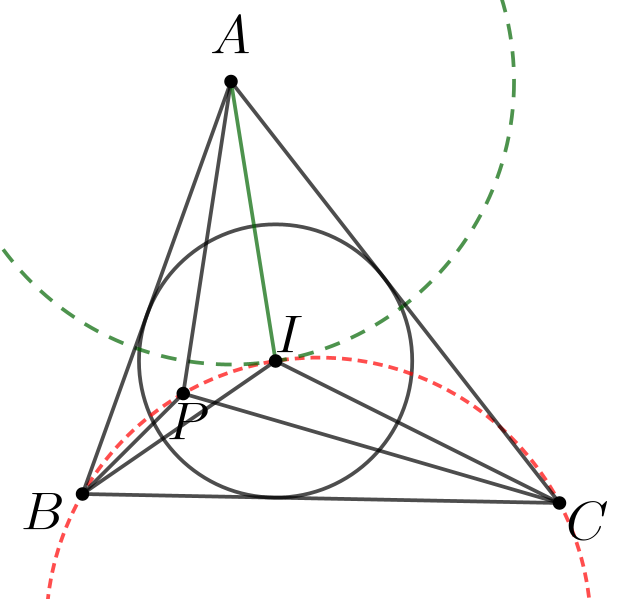
分析：对等式两边移项, \(\small \angle PBA-\angle PBC=\angle PCB-\angle PCA\),由等式两边的符号相同可推出点\(\small P\)落在\(\small \triangle IBC\)外, 合理猜测\(\small P,B,C,I\)四点共圆, 结合鸡爪定理可验证满足题意.

证：

\[\small \begin{align*}\angle PBA+\angle PCA&=\angle IBA-\angle IBP+\angle ICA+\angle ICP\\&=\angle IBC-\angle IBP+\angle ICB+\angle ICP\\&=\angle IBC+\angle ICB-\angle IBP+\angle ICP\\&=180^\circ -\angle BIC-\angle IBP+\angle ICP\\\angle PBC+\angle PCB&=180^\circ -\angle BPC\\\Rightarrow \angle BPC+\angle ICP&=\angle BIC+\angle IBP \\ \Rightarrow 180^\circ-\angle PDB-\angle IBP&+\angle ICP=180^\circ-\angle IDC-\angle ICP+\angle IBP, \end{align*} \]

因为\(\small \angle PDB=\angle IDC\),所以上式两边抵消可得\(\small \angle IBP= \angle ICP\), 这说明\(\small P,B,C,I\)四点共圆. 由鸡爪定理可知, \(\small AP\ge AI\), 等号成立当且仅当\(\small P=I\).

注： 鸡爪定理在证明过程中不能直接使用, 需证明后才能使用, 因(比较懒)篇幅原因证明略.

引理4(西姆松线) 如图, 设\(\small P\)是\(\small \triangle ABC\)外接圆上任一点, \(\small X,Y,Z\)分别是从\(\small P\)到直线\(\small BC,CA,AB\)的投影. 证明：\(\small X,Y,Z\)共线.

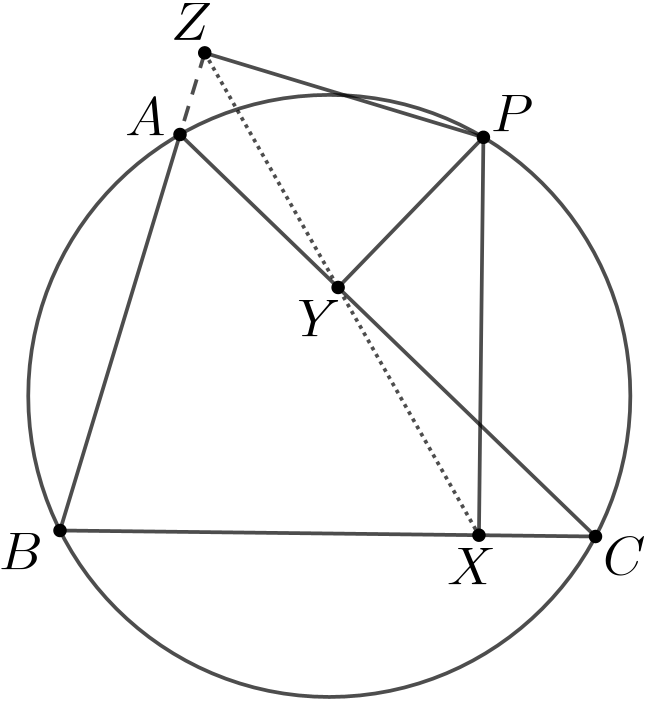
证： 根据垂直关系得到点\(\small P\)在三个圆\(\small (YZA),(ZXB),(XYC)\)上, 易得

\[\small\begin{align*} \measuredangle PYZ & =\measuredangle PAZ=\measuredangle PAB\\ &=\measuredangle PCB=\measuredangle PCX=\measuredangle PYX. \end{align*} \]

所以\(\small X,Y,Z\)三点共线.

问题4(USAMO 2010/1) 设凸五边形\(\small AXYZB\)内接于以\(\small AB\)为直径的半圆. 记\(\small P,Q,R,S\)分别是\(\small Y\)到直线\(\small AX,BX,AZ,BZ\)上的投影. 证明：直线\(\small PQ\)和\(\small RS\)形成的锐角是\(\small \angle XOZ\)的一半, 其中\(\small O\)是线段\(\small AB\)的中点.

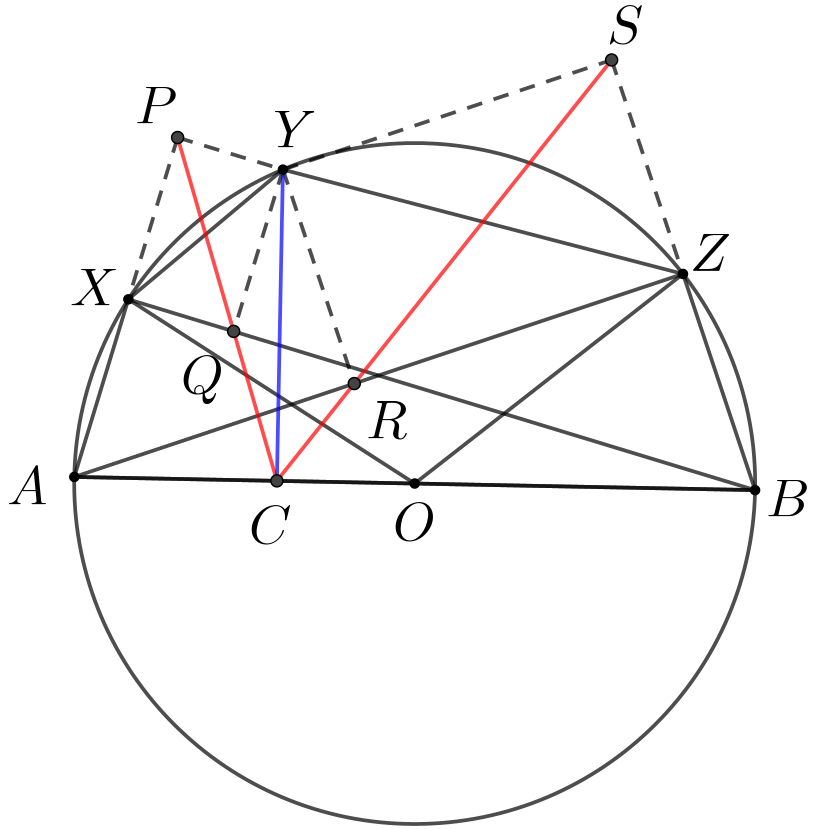
证： 作\(\small YC\perp AB\)于\(\small C\), 根据西姆松引理可得\(\small P,Q,C\)与\(\small S,R,C\)三点共线. 由题目条件易知\(\small A,P,Y,C\)四点共圆, \(\small C,Y,S,B\)四点共圆, 于是我们有\(\small \angle PCY=\angle XAY=\angle XBY,\angle SCY=\angle ZBY\), 此时,

\[\small \begin{align*} \small \angle PCS&=\angle PCY+\angle SCY\\ &=\angle XBY+\angle ZBY\\ &=\angle ZBX=\frac{1}{2}\angle XOZ. \end{align*} \]

问题5(IMO 2013/4) 设锐角\(\small \triangle ABC\)的垂心为\(\small H,W\)是边\(\small \overline{BC}\)上一点, 位于\(\small B,C\)中间. 点\(\small M,N\)分别是从\(\small B,C\)引出的三角形的高的垂足. \(\small \omega_1\)是\(\small \triangle BWN\)的外接圆, 点\(\small X\)满足\(\small \overline{WX}\)是\(\small \omega_1\)的直径. 类似地, 点\(\small Y\)满足\(\small \overline{MY}\)是\(\small \triangle CWM\)外接圆\(\small \omega_2\)的直径. 证明：点\(\small X,Y,H\)共线.

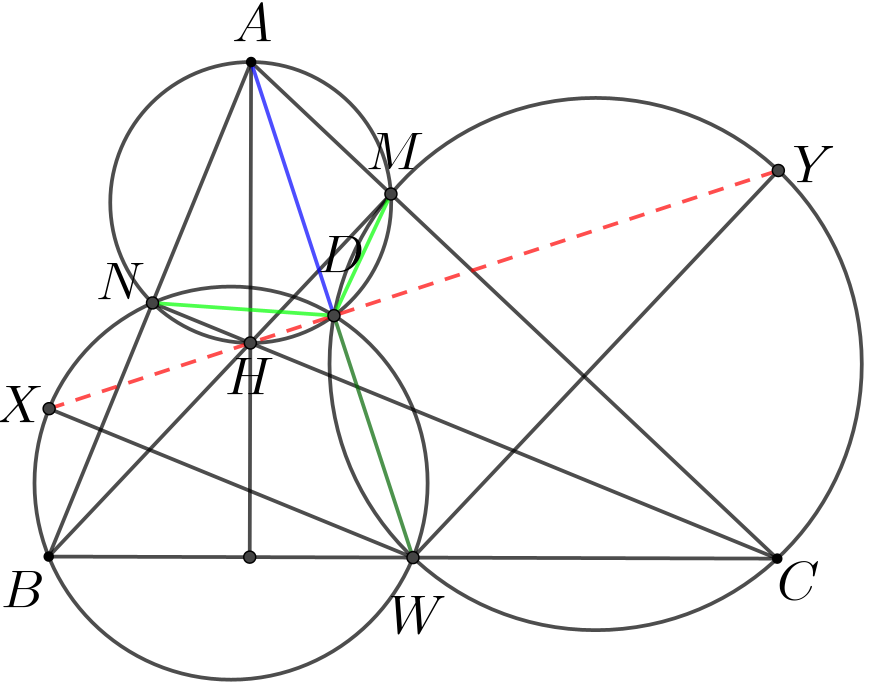
证： 设\(\small \omega_1\)与\(\small \omega_2\)相交于另一点\(\small D\), 因为\(\small \angle XDM=\angle YDW=90^\circ\), 所以\(\small X,D,Y\)三点共线. 下面只需证明\(\small H\)在直线\(\small XD\)上. 注意到\(\small \angle ADN+\angle ADM=\angle ABC+\angle ACB=180^\circ-\angle BAC\), 所以\(\small A,N,D,M\)四点共圆, 又因为\(\small A,N,H,M\)四点共圆, 所以\(\small A,N,H,D,M\)五点共圆, 此时\(\small AH\)是直径, 所以\(\small AD\perp HD\),所以\(\small H\)在直线\(\small XD\)上. 于是\(\small X,H,Y\)三点共线.

注：\(\small D\)称作密克点，后期文章补充(给自己挖坑).

问题6(IMO 1985/1]) 某个圆的圆心在圆内接四边形\(\small ABCD\)的边\(\small \overline{AB}\)上, 并且与另外三边相切. 证明：\(\small AD+BC=AB\).

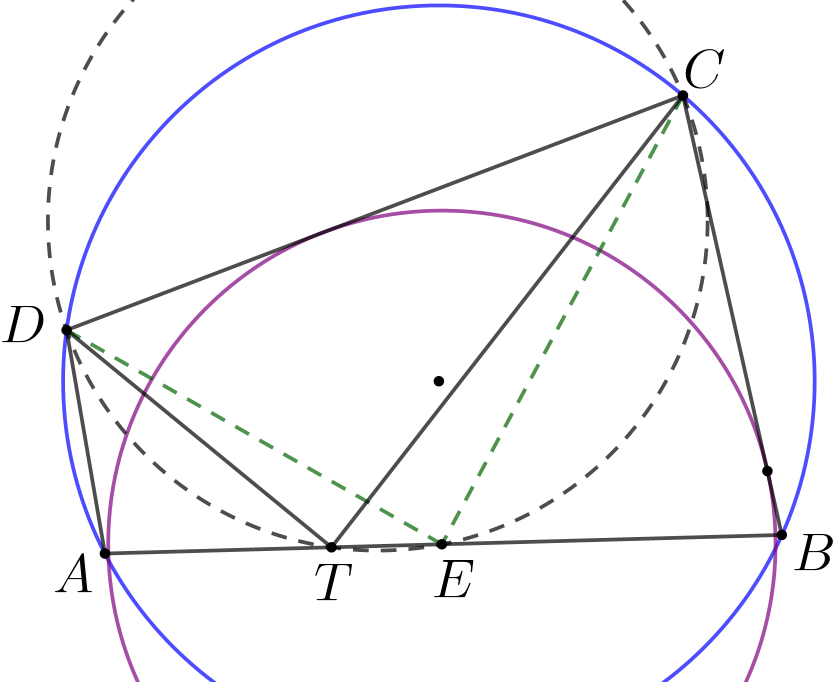
证： 在\(\small AB\)上作点\(\small T\)满足\(\small AD=AT\), 那么\(\small \angle DTA=\frac{1}{2}(\pi -\angle DAB)=\frac{1}{2}\angle DCB=\angle DCE\),这说明\(\small D,C,E,F\)四点共圆, 于是我们有\(\small \angle CTB=\angle CDE=\frac{1}{2}\angle CDA=\frac{1}{2}(\pi-\angle ABC)\),这说明\(\small TB=BC\), 所以\(\small AD+BC=AT+TB=AB\).