这下罄竹难书了

由四个金牌命制的联赛模拟试卷，使我校高二高三竞赛班取得了一试最高 84 分，加试最高 160 分的好成绩！

一试

一、填空题

1. 如图是一个 \(4\times 4\) 的正方形方格表，则最少需要 \(\text{_____}\) 条直线，才能使得每个方格都被至少一条直线穿过。

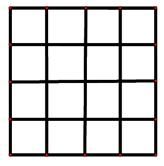
2. 设复数 \(z\) 满足：\(\frac{z-20}{\bar z+24}\) 是纯虚数，则 \(|z-11|\) 的取值范围是 \(\text{_____}\) 。

3. 设 \(P\) 为椭圆 \(C_1:\frac{x^2}{24}+\frac{y^2}{20}=1\) 上一点，过 \(P\) 作 \(C_1\) 的切线交圆 \(C_2:x^2+y^2=24\) 于 \(A,B\) 两点（\(A\) 点在左侧）。若 \(F_1,F_2\) 分别为 \(C_1\) 的左、右焦点，则四边形 \(AF_1F_2B\) 的面积最大值为 \(\text{_____}\) 。

4. 对所有实数 \(x,y\)，定义 \(x\star y=\frac{x+y}{1+xy}\)。则 \((\cdots(((2\star 3)\star 4)\star 5)\star \cdots)\star 2024=\text{_____}\) 。

5. 设三个互不相等的实数 \(a,b,c\) 满足 \(a+b+c=0\)，且 \(a^2-b=b^2-c=c^2-a\)，则 \(ab+bc+ca=\text{_____}\) 。

6. 设 \(A,B,C\) 是一个三角形的三个内角，则 \((3\sin B+4\sin C)\cos A\) 的最小值为 \(\text{_____}\) 。

7. 机场为旅客提供的圆锥形纸杯如图所示。该圆锥母线长为 \(12\text{cm}\)，底面直径为 \(8\text{cm}\)。旅客使用纸杯喝水时，当水面与纸杯内壁所形成的椭圆经过母线中点时，椭圆的离心率等于 \(\text{_____}\) 。

8. 给定正整数 \(n\)。对于一个 \(1,2,\cdots,2n\) 的排列，定义其分数为：将排列划分为两个等长的子序列，对应项乘积和的最大值。则分数取到最大值的排列数目为 \(\text{_____}\) 。

二、解答题

9. 已知双曲线 \(C:y^2-x^2=1\)，上顶点为 \(D\)。一直线与双曲线 \(C\) 的两支分别交于 \(A,B\) 两点，与 \(x\) 轴交于 \(T\)，且 \(B\) 在第一象限。设直线 \(DB\) 与 \(x\) 轴交于点 \(E\)。若直线 \(DB\) 的倾斜角为 \(\frac{\pi}{6}\)，证明：\(\ang ADT=\frac{\pi}{6}\)。

10. 设 \(a_1,a_2,\cdots,a_k\) 为有穷整数数列，满足：对任意正整数 \(n\in\{1,2,\cdots,20\}\)，存在 \(1\le l\le r\le k\)，使得 \(\sum_{i=l}^{r}a_i=n\)，且 \(\sum_{i=1}^{k}a_i\lt 20\)。求 \(k\) 的最小值。

11. 设 \(a_0,a_1,a_2,\cdots\) 是实数列，满足对任意 \(i\in \N\)，均有 \(a_{i+1}=[a_i]\{a_i\}\)。证明：对充分大的 \(i\)，有 \(a_i=a_{i+2}\)。

加试

一、已知 \(\triangle ABC\) 中，\(CA=CB\)。点 \(E\) 在 \(\triangle ABC\) 的外接圆上，满足 \(\ang ECB =90^{\circ}\)。过 \(E\) 做 \(BC\) 的平行线交 \(AC,AB\) 分别于 \(F,G\)，证明：\(\triangle EGB\) 的外心在 \(\triangle ECF\) 的外接圆上。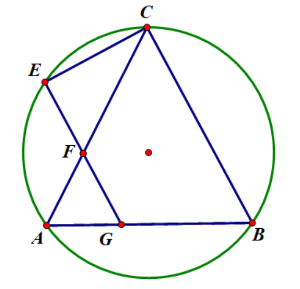

二、在一个无穷大的方格表内，放置着 \(n^2\) 枚棋子，构成了一个 \(n\times n\) 的方阵。一个“三连”指的是在横方向或竖方向上相连的三个格子。一次操作定义为：选择一个恰含两枚相邻棋子的“三连”，拿走这两枚棋子，然后在“三连”中原本没有棋子的方格内放上一枚棋子，如图所示。求最多能进行的操作数目。

三、设 \(n\ge 2\) 为一个正整数，对 \(2\le i\le n\)，\(a_i\) 等概率取 \(1,2,\cdots,i-1\) 之一。定义序列 \(d\) 满足：\(d_1=0,d_{i}=d_{a_i}+1(2\le i\le n)\)。设随机变量 \(X\) 表示 \(d_1,d_2,\cdots,d_n\) 中的最大值，证明：存在与 \(n\) 无关的正常数 \(c_1,c_2\)，使得 \(c_1\ln n\le E(X)\le c_2\ln n\)。

四、 求所有的正整数 \(n\)，使得 \(\tau(n)\mid 2^{\sigma(n)}-1\)。