P2757 [国家集训队] 等差子序列 和 CF452F Permutation

题意：

给定一个长度为 \(n\) 的排列 \(a\)，判断其中是否有长度 \(\ge 3\) 的等差数列。

\(1 \le n \le 5 \times 10^5\)。

思路：

首先若存在长度 \(>3\) 的等差数列，则其中的一部分肯定由长度为 \(3\) 的等差数列组成；即我们现在只需要判断是否存在长度为 \(3\) 的等差数列即可。

考虑枚举中间的数 \(a_i\)，则问题转化为 \(a_i-k\) 与 \(a_i + k\) 是否同时出现在 \(i\) 的两侧。

注意到 \(a\) 是一个排列，则是没有重复数字的。

那么我们可以记作若 \(i\) 左边的 \(a_j\) 出现过，则将标记数组中第 \(a_j\) 个位置为 \(0\)。

若不可以构成等差数列的话，当 \(a_i-k\) 被标记了，则 \(a_i+k\) 也必须被标记（不然就会出现在 \(i\) 右侧，形成等差数列），那么标记数组就是以 \(i\) 为回文中心回文的。

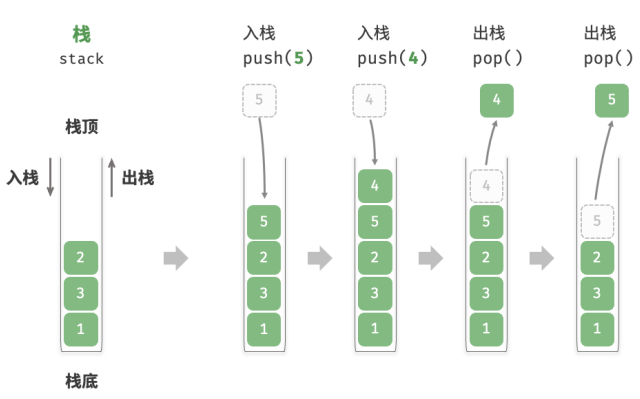
现在我们需要支持单点赋值为 \(1\)，判断一个区间是否是回文的；可以直接线段树维护翻转后和未翻转时的哈希值，判断是否相等即为回文。

时间复杂度为 \(O(N \log N \log W)\)。

完整代码：