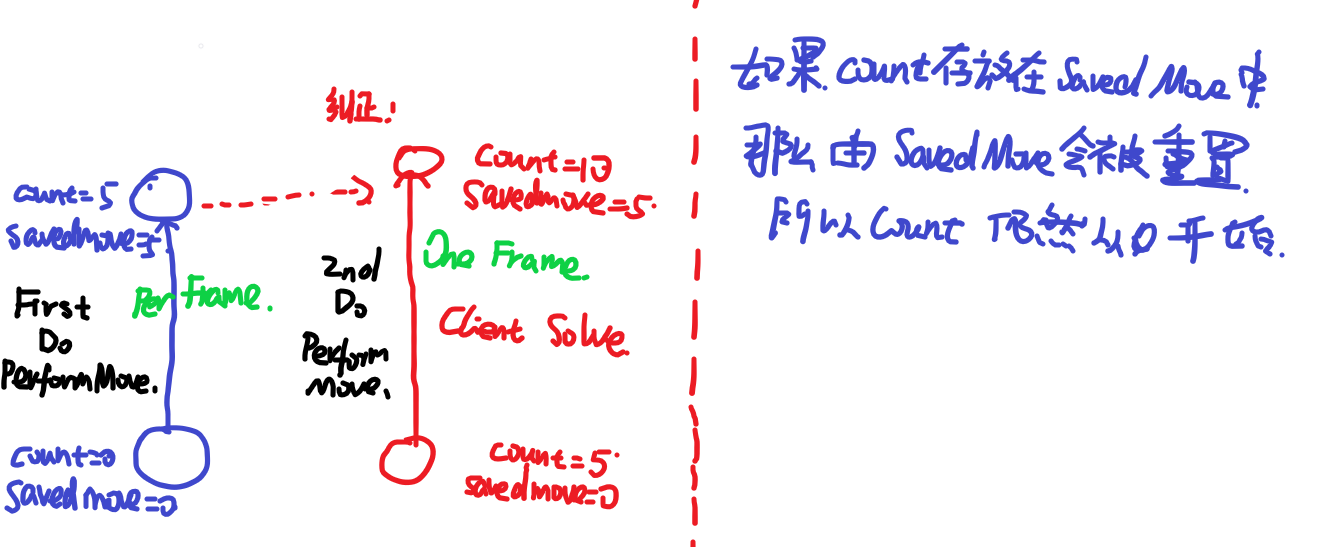
树形图的定义:没有环,每个点(除了根节点)的入度都是\(1\),根节点的入度为\(0\)
朱刘算法的过程见OI-wiki;当没有环的时候,就满足了树形图的定义,于是可以结束;否则的话就将所有环缩点(注意此时由于每个点的入度都是\(1\),所以不可能存在两个环有公共点和公共边)得到新图\(G_1\),对于\(G_1\)中的边,有三类:如果是缩点点内部的边(也就是环上的边)那么就删去,如果是终点在缩点点内部的边(也就是终点是环上的点),那么边权为原边权减去终点所选择的那条入边的权值,如果是其余边就不变
比如
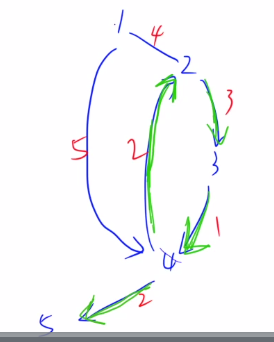
变成

最终答案就是所有选的边的边权和
证明:如果最开始的选择之后无环,那么肯定是最小树形图(达到了下界);否则的话,先看看两个引理
引理一:对图中任意一个环,至少去掉一条边
这个显然
引理二:存在一个最小树形图,使得每个环只去掉一条边
证:如果对任意一个最小树形图,都存在一个环至少去掉两条边,我们找出这个环,假设这个环是\(x_0-x_1-···-x_k-x_0\),不妨设\(x_k-x_0\)和\(x_i-x_{i+1}\)这两条边被去掉了;对当前的最小树形图,肯定可以从跟走到\(x_0\)再从\(x_0\)走到\(x_i\),现在考虑\(x_{i+1}\)的入边,我们将这条入边删掉,换成\((x_i,x_{i+1})\),显然还是一个最小树形图,而且边权和变小,矛盾;于是得证
根据引理二,我们找出原图中所有满足每个环只去掉一条边的树形图,设他们组成的集合是\(S\),那么\(S\)中边权和最小的就是答案;我们再考虑将原图的环缩点之后得到的新图\(G_1\)的所有最小树形图组成的集合是\(S_1\),不难知道\(S\)和\(S_1\)一一对应(包括权值都是相同的),于是转化成求\(G_1\)的最小树形图;所以递归求解就好了