队列
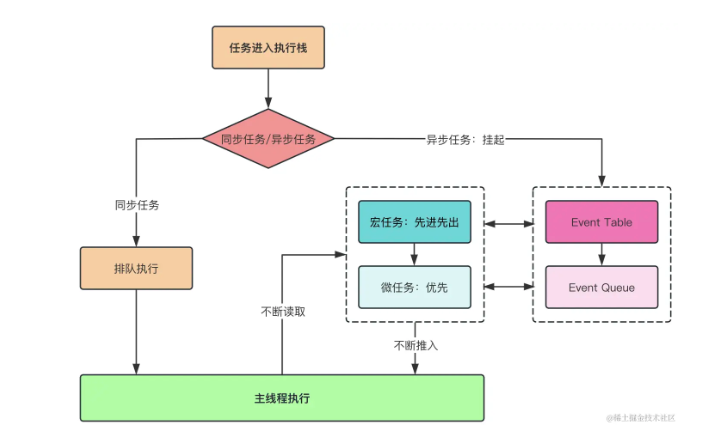
队列(queue)是一种遵循先入先出规则的线性数据结构。队列模拟了排队现象,即新来的人不断加入队列尾部,而队列头部的人逐个离开。
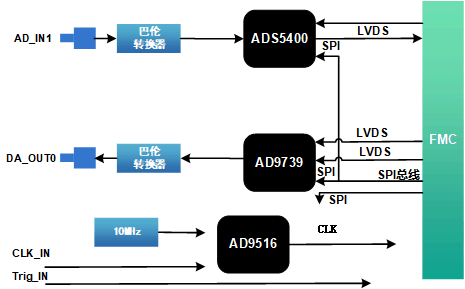
如图所示,我们将队列头部称为“队首”,尾部称为“队尾”,将把元素加入队列尾部的操作称为“入队”,删除队首元素的操作称为“出队”。
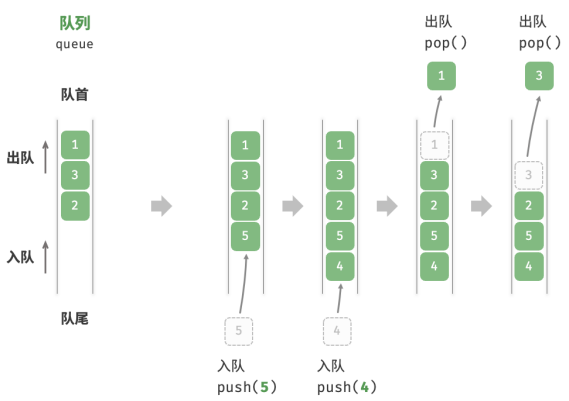
队列常用操作
| 方法名 | 描述 | 时间复杂度 |
| push() | 元素入队,即将元素添加至队尾 | O(1) |
| pop() | 队首元素出队 | O(1) |
| peek() | 访问队首元素 | O(1) |
我们可以直接使用C++中现成的队列类:
/*初始化队列*/queue<int> que;/*元素入队*/que.push(1);que.push(3);que.push(2);que.push(5);que.push(4);/*访问队首元素*/int que_front = que.front();cout << "队首元素:" << que_front << endl;/*元素出队*/cout << "元素出队" << endl;que.pop();cout << "队首元素:" << que.front() << endl;/*获取队列的长度*/int que_size = que.size();cout << "队列长度:" << que_size << endl;/*判断队列是否为空*/bool que_empty = que.empty();cout << "队列是否为空:" << que_empty << endl;队列实现
基于链表的实现
我们可以将链表的“头结点”和“尾节点”分别视为“队首”和“队尾”,规定队尾仅可以添加节点,队首仅可删除节点。
struct ListNode{int val;ListNode* next;ListNode(int x) :val(x), next(nullptr){}
};class LinkedListQueue{
private:ListNode *front; // 头节点ListNode *rear; // 尾节点int queSize; // 队列长度
public:LinkedListQueue(){front = nullptr;rear = nullptr;queSize = 0;}~LinkedListQueue(){while (front != nullptr){ListNode *tmp = front;front = front->next;delete tmp;}}/*获取队列长度*/int size(){return queSize;}/*判断队列是否为空*/bool isEmpty(){return (size() == 0);}/*入队*/void push(int num){ListNode *node = new ListNode(num);if (isEmpty()){front = node;rear = node;}else{rear->next = node;rear = node;}queSize++;}/*出队*/int pop(){int num = peek();ListNode *tmp = front;front = front->next;delete tmp;queSize--;return num;}/*访问队首元素*/int peek(){if (isEmpty())throw out_of_range("队列为空");return front->val;}
};基于数组的实现
在数组中删除首个元素的时间复杂度为O(n),这会导致出队操作效率低。但我们可以采用以下这个巧妙方法避免这个问题。
我们使用一个变量front指向队首元素的索引,并维护一个变量size用于记录队列长度。定义rear = front + size,这个公式计算出的rear指向队尾元素之后的下一个位置。
基于此设计,数组中包含元素的有效区间为[front, rear - 1]
- 入队操作:将输入元素赋值给
rear索引处,并将size增加1。 - 出队操作:只需将
front增加1,并将size减少1。
这样,入队和出队操作都只需要进行一次操作,时间复杂度均为O(1)。
但在不断进行入队和出队过程中,front和rear都在向右移动,当它们到达数组尾部时就无法移动了。为解决此问题,我们可以将数组视为收尾相接的“环形数组”。
对于环形数组,我们需要让front和rear在越过数组尾部时,直接回到数组头部继续遍历。这种周期性规律可以通过“取余操作”来实现。
/*基于环形数组实现的队列*/
class ArrayQueue{
private:int * nums; // 用于存储队列元素的数组int front; // 队首指针 ,指向队首元素int queSize; // 队列长度int queCapacity; // 队列容量
public:ArrayQueue(int capacity){nums = new int[capacity];queCapacity = capacity;front = 0;queSize = 0;}~ArrayQueue() {delete nums;}/*获取队列的容量*/int capacity(){return queCapacity;}/*获取队列长度*/int size(){return queSize;}/*判断队列是否为空*/bool isEmpty(){return (queSize == 0);}/*入队*/void push(int num){if (queSize == queCapacity){cout << "队列已满" << endl;return;}// 通过取余操作实现 rear 越过数组尾部后回到头部int rear = (front + queSize) % queCapacity;nums[rear] = num;queSize++;}/*出队*/int pop(){int num = peek();// 队首指针向后移动一位,若越过尾部,则返回到数组头部front = (front + 1) % queCapacity;queSize--;return num;}/*访问队首元素*/int peek(){if (isEmpty())throw out_of_range("队列为空");return nums[front];}};以上实现的队列仍然具有局限性:其长度不可变;可以将数组替换为动态数组,从而引入扩容机制。
队列典型应用
- 淘宝订单。购物者下单后,订单将加入队列中,系统随后会根据顺序处理队列中的订单。在双十一期间,短时间内会产生海量订单,高并发称为工程师们需要重点攻克的问题。
- 各类代办事项。任何需要实现“先来后到”功能的场景,例如打印机的任务队列、餐厅的出餐队列等,队列在这些场景中可以有效地维护处理顺序。
双向队列
在队列中,我们仅能删除头部元素或在尾部添加元素。双向队列(double-ended queue)提供了更高的灵活性,允许在头部和尾部执行元素的添加或删除操作。
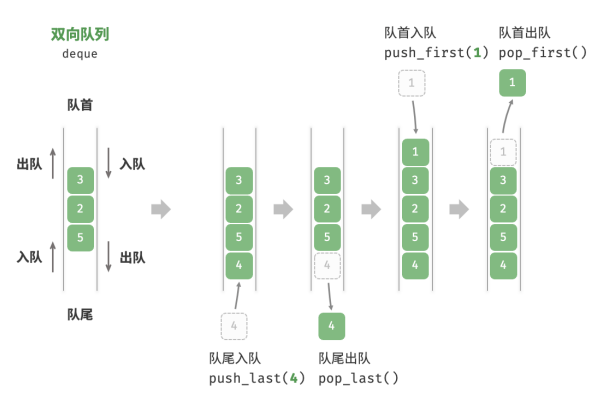
| 方法名 | 描述 | 时间复杂度 |
| push_front() | 将元素添加至队首 | O(1) |
| push_back() | 将元素添加至队尾 | O(1) |
| pop_front() | 删除队首元素 | O(1) |
| pop_back() | 删除队尾元素 | O(1) |
| front() | 访问队首元素 | O(1) |
| back() | 访问队尾元素 | O(1) |
我们可以直接使用C++中已实现的双向队列类:
deque<int> que;/*元素入队*/que.push_back(2);que.push_back(5);que.push_back(4);que.push_front(3);que.push_front(1);/*访问元素*/int front = que.front(); // 队首元素int back = que.back(); // 队尾元素cout << "队首元素:" << front << endl;cout << "队尾元素:" << back << endl;/*元素出队*/que.pop_front(); //队首元素出队cout << "队首元素出队" << endl;que.pop_back(); // 队尾元素出队cout << "队尾元素出队" << endl;cout << "队首元素:" << que.front() << endl;cout << "队尾元素:" << que.back() << endl;/*获取双向队列的长度*/int size = que.size();cout << "队列长度:" << size << endl;/*判断双向队列是否为空*/bool empty = que.empty();cout << "是否为空 : " << empty << endl;