一.机器学习的定义和核心
1.机器学习就是让机器具备找一个函数的能力。机器具备找函数的能力以后,它可以做很多事。
2.在机器学习领域里面,除了回归跟分类以外,还有结构化学习(structured learning)。机器不只是要做选择题或输出一个数字,而是产生一个有结构的物体,比如让机器画一张图,写一篇文章。这种叫机器产生有结构的东西的问题称为结构化学习。
3.机器学习找函数的过程,分成 3 个步骤。第一个步骤是写出一个带有未知参数的函数 f,其能预测未来观看次数。比如将函数写成
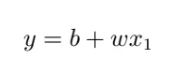
其中,y 是准备要预测的东西,y 跟 x1 都是数值,b 跟 w 是未知的参数,它是准备要通过数据去找出来的,w 跟 b 是未知的,只是隐约地猜测。猜测往往来自于对这个问题本质上的了解,即领域知识(domain knowledge)。机器学习就需要一些领域知识。总之,y = b + w ∗ x1,而 b 跟 w 是未知的。带有未知的参数(parameter)的函数称为模型(model)。模型在机器学习里面,就是一个带有未知的参数的函数,特征(feature) x1 是这个函数里面已知的而 w 跟 b 是未知的参数。w 称为权重(weight),b 称为偏置(bias)。这个是第一个步骤。
第 2 个步骤是定义损失(loss),损失也是一个函数。这个函数的输入是模型里面的参数,模型是 y = b + w ∗ x1,而 b 跟 w 是未知的,损失是函数 L(b, w),其输入是模型参数 b 跟w。损失函数输出的值代表,现在如果把这一组未知的参数,设定某一个数值的时候,这笔数值好还是不好。举一个具体的例子,假设未知的参数的设定是 b = 500,w = 1,预测未来的观看次数的函数就变成 y = 500 + x1。
估测的值跟实际的值之间的差距,其实有不同的计算方法,计算 y 与 yˆ 之间绝对值的差距,称为平均绝对误差(Mean Absolute Error,MAE)。如果算 y 与 yˆ 之间平方的差距,则称为均方误差(Mean SquaredError,MSE)。
有一些任务中 y 和 yˆ 都是概率分布,这个时候可能会选择交叉熵(cross entropy),这个是机器学习的第 2 步。
接下来进入机器学习的第 3 步:解一个最优化的问题。找一个 w 跟 b,把未知的参数找一个数值出来,看代哪一个数值进去可以让损失 L 的值最小,就是要找的 w 跟 b,这个可以让损失最小的 w 跟 b 称为 w∗ 跟 b∗ 代表它们是最好的一组 w 跟 b,可以让损失的值最小。梯度下降(gradient descent)是经常会使用优化的方法。为了要简化起见,先假设只有一个未知的参数 w,b 是已知的。w 代不同的数值的时候,就会得到不同的损失,这一条曲线就是误差表面。这一步的步伐的大小取决于两件事情:
(a)第一件事情是这个地方的斜率,斜率大步伐就跨大一点,斜率小步伐就跨小一点。
(b)另外,学习率(learning rate)η 也会影响步伐大小。学习率是自己设定的,如果 η 设大一点,每次参数更新就会量大,学习可能就比较快。如果 η 设小一点,参数更新就很慢,每次只会改变一点点参数的数值。这种在做机器学习,需要自己设定,不是机器自己找出来的,称为超参数(hyperparameter)。
梯度下降有一个很大的问题,没有找到真正最好的解,没有找到可以让损失最小的 w。图示如下:
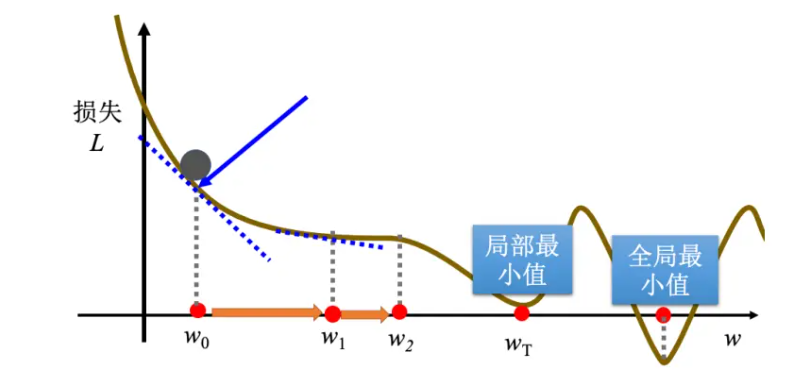
右侧红点这个位置是真的可以让损失最小的地方,称为全局最小值(global minima),而 wT 这个地方称为局部最小值(local minima),其左右两边都比这个地方的损失还要高一点,但是它不是整个误差表面上面的最低点。所以常常可能会听到有人讲到梯度下降不是个好方法,这个方法会有局部最小值的问题,无法真的找到全局最小值。事实上局部最小值是一个假问题,在做梯度下降的时候,真正面对的难题不是局部最小值。有两个参数的情况下使用梯度下降,其实跟刚才一个参数没有什么不同。如果一个参数没有问题的话,可以很快的推广到两个参数。
在深度学习框架里面,比如 PyTorch 里面,算微分都是程序自动帮计算的。就是反复同样的步骤,就不断的更新 w 跟 b,期待最后,可以找到一个最好的 w,w∗ 跟最好的 b∗。