A - Haiku
直接模拟。
#include <bits/stdc++.h>using namespace std;
using i64 = long long;int main() {ios::sync_with_stdio(false), cin.tie(nullptr);string s;cin >> s;string a, b, c;a = s.substr(0, 5);b = s.substr(6, 7);c = s.substr(14);cout << a << " " << b << " " << c;return 0;
}
B - Sum of Three Integers
暴力做的话是三重循环会超时,可以枚举前两个数,然后判断第三个数是否合法即可,时间复杂度为 \(O(n^2)\)。
#include <bits/stdc++.h>using namespace std;
using i64 = long long;int main() {ios::sync_with_stdio(false), cin.tie(nullptr);int K, S;cin >> K >> S;int ans = 0;for (int i = 0; i <= K; i++) {for (int j = 0; j <= K; j++) {int k = S - i - j;if (k >= 0 && k <= K) ans++;}}cout << ans;return 0;
}
C - Back and Forth
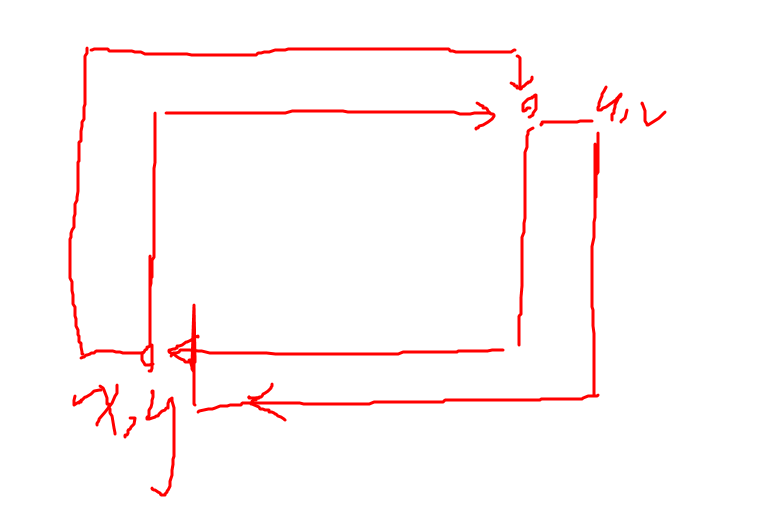
本题看着吓人,其实只需要找到一条互相不重复的路线即可,不妨就以样例 \(1\) 为例。画出图形,然后模拟即可。
#include <bits/stdc++.h>using namespace std;
using i64 = long long;int main() {ios::sync_with_stdio(false), cin.tie(nullptr);int x, y, u, v;cin >> x >> y >> u >> v;for (int i = y; i < v; i++) cout << 'U';for (int i = x; i < u; i++) cout << 'R';for (int i = v; i > y; i--) cout << 'D';for (int i = u; i > x; i--) cout << 'L';cout << 'L';for (int i = y; i < v + 1; i++) cout << 'U';for (int i = x - 1; i < u; i++) cout << 'R';cout << "DR";for (int i = v; i > y - 1; i--) cout << 'D';for (int i = u + 1; i > x; i--) cout << 'L';cout << 'U';return 0;
}
D - Candidates of No Shortest Paths
\(\rm Floyd\) 算法,之后会补。