Pinely Round 4 (Div. 1 + Div. 2) VP记录
场上打了 ABCDF,被 E 二粉兔创飞了。
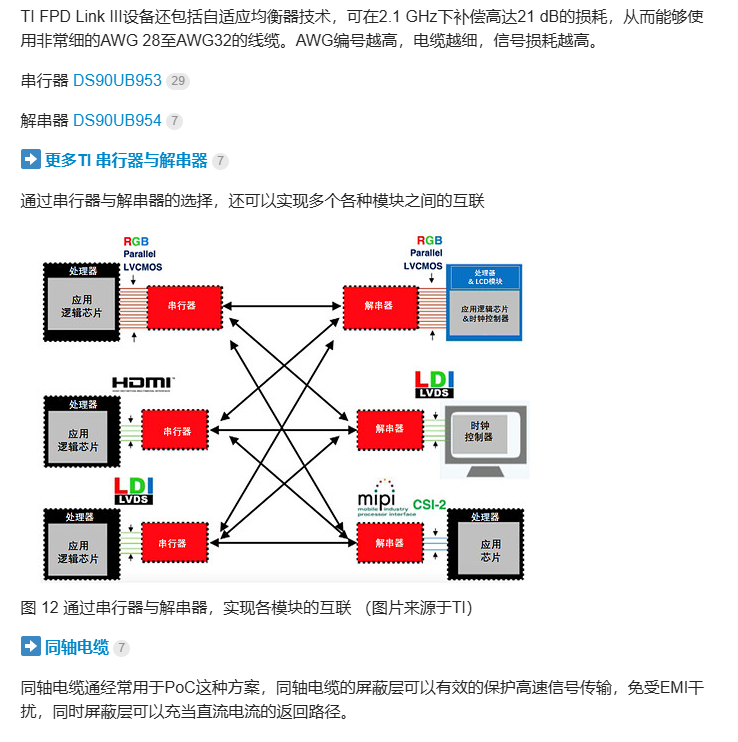
这场的构造题有:B D E G I,乐死了。
A
把数列黑白染色,第一个格为黑色,那么每次删除会删除一个黑格子和一个白格子。而黑格子始终比白格子多一个,因此最后选到的是黑格子。答案极为黑格子的最大值,也易证一定存在这样的构造。
B
我发现这种位运算构造是我的弱势区。很逆天的写了 25 分钟,相比下 C 写了 5 分钟。
一开始初始化所有 \(a\) 为 \(0\),枚举 \(b_i\) 后令 \(a_{i}\) 和 \(a_{i + 1}\) 按位或上当前的 \(b_i\) 即可。
C
每次用最大值和最小值的 mid 操作,这样每次操作后值域会减半。
最后检查数组是否全为 \(0\) 判掉无解即可。
D
考虑把数分为奇数和偶数两类。
质数除了 \(2\) 都是奇数。同奇偶性异或同奇偶性是偶数否则是奇数。
如果把 \(2\) 看成合数,那这张图是二分图,这个时候可以黑白染色。
但实际上不行,因为有 \(2\) 的参与。
如果两个数字异或起来等于 \(2\),那么这两个数字不能是同色。也就是,对于一组数 \(a, a + 1, a + 2, a + 3\),其中 \(a\) 是 \(4\) 的倍数,第一个数和第三个数不能同色,第二个数和第四个数不能同色。
所以一定能四染色,\(i\) 号点染 \((i \bmod 4) + 1\) 即可。
E
为什么我 D 能想到二分图但是 E 想不到呢。。
注意到如果题目不是二分图,它不能进行二染色,那么我们只要选 Alice 后一直给Bob 同样的两种颜色逼着 Bob 要对一个非二分图二染色,然后就赢了。
否则选 Bob 能必胜。考虑二分图的左部点和右部点,各给它们一种颜色对应。那么 Alice 的三选二必然会给出一种对应一部分的颜色,那么如果这个时候那部分点还有剩就直接拿出来染成对应颜色就行了,否则把另一部分染成 Alice 给的 另一种颜色。
F
判能不能形成三角形,一般有个折半 trick。
就是,将一个区间的小棒长度排序后,从大到小看,如果当前最大的三个数不能组成三角形,也就是 \(a_i \ge a_{i - 1} + a_{i - 2} \implies a_i \ge 2a_{i - 2}\),所以两步后值域减半。
然后这个数列最坏情况是斐波那契数列,所以大概看看如果区间长度大于 \(50\) 就一定可以组成两个三角形。(场上我用的 \(100\) 判断,因为没细分析)
那么区间长度小于 \(50\) 了,就可以随便做了,好像有人 \(O(k^3)(k = 50)\) 过了。
但是有 \(O(k)\) 的做法。首先先尝试拿走最大的三角形后能否再拿一个,先把这种情况判掉。
如果不行,那有可能是两个三角形卡在一起了,例如样例的 \([5, 2, 2, 10, 4, 10]\)。
那么因为我们排序了,所以如果存在这种情况,必定能在一段连续的 \(6\) 根小棒中找到,所以对 \(\binom{5}{2}\) 种情况暴力判断一下即可。
G
把原图分成这样的四个区域。
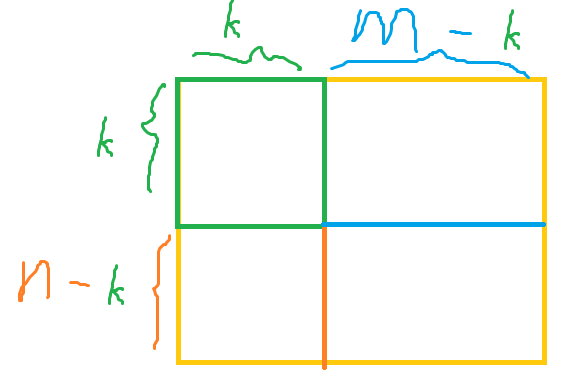
令水平操作只放在左侧 \(k\) 列,垂直操作只摆在上方 \(k\) 列。
如果左下角区域和右上角区域没填完,就优先填这两块区域,否则填左上角的区域,优先填能导致消除的区域。
感性理解或者手摸一下,这么填能进行任意多次操作。(不是很会证明,但是自己在图上玩一下就大概感觉出它是对的)
然后模拟这一过程即可,这题变成了大模拟,但是也没那么大模拟。
暴力改能单次询问询问 \(O(nm)\),随便过了。
H
待补。
I
待补牛魔。