题目求的就是点仙人掌的数量;点仙人掌的所有环缩点之后就变成了一棵树,于是考虑无根树的数量怎么求,很显然利用Prufer序列就好了;然后考虑怎么将Prufer序列移植到点仙人掌上面,此时就要利用扩展Prufer序列
扩展Prufer序列:对于一个点仙人掌来说,先将所有环缩点变成一棵树,然后将所有缩点离散化(就是重新编号),指定编号最大的为根;执行Prufer操作,首先选择一个度数为\(1\)的且编号最小的缩点,删除其,并向prufer序列中添加其与父亲的连边的另一端点(注意另一端点是原图上的点,不是缩点的编号),并重复以上的操作,如下
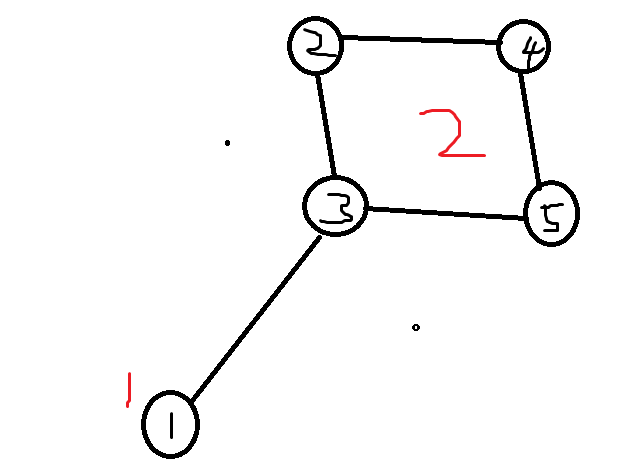
黑色是原图的编号,红色是缩点的编号;我们最开始选择缩点\(1\),然后发现另一端是点\(3\),于是prufer序列的第一个为\(3\)(不是\(2\))
由以上过程可知,如果我们知道了Prufer序列,有多少个缩点,每个点在哪个缩点内部,就可以唯一确定这个仙人掌;所以我们只需要解决以上三个问题就好了
有多少个缩点:枚举就好了,设有\(i\)个缩点,于是\(1\leq i\leq n\);为了方便,我们设点\(n\)所在的缩点编号为\(i\)(这样是为了不重复计数)
每个点在哪个缩点内部:利用递推解决。设\(f[i][j]\)表示将\(i\)个点分为\(j\)个缩点,并且每个缩点不是根(也就是说每个缩点都有父亲)的方案数。$$f[i][j]=\overset{i-j}{\underset{k=0}{\sum}}\binom{i-1}{k}\frac{(k+1)!}{2}f[i-k-1][j-1]$$
,这一式子的意义是:我们假设第\(j\)个缩点包含\(i\),从\(1\) ~ \(i-1\)中选出\(k\)个点与\(i\)一起在缩点\(j\)中;考虑圆排列的个数是\(k!\),由于翻转是同一种,所以总数即\(\frac{k!}{2}\),而缩点\(j\)是有父亲的,于是选择一个点与父亲相连,乘以\(k\);最后剩下\(i-k-1\)个点分成\(j-1\)个缩点(注意我们不的缩点大小要么是\(1\),要么不低于\(3\),也就是不能为\(2\),至于为什么下面说)
Prufer序列的个数:这个比较简单,为\(n^{i-2}\)
最终的答案:$$ans=\frac{(n-1)!}{2}+\overset{n}{\underset{i=2}{\sum}}\overset{n-i}{\underset{j=0}{\sum}}\binom{n-1}{j}\frac{j!}{2}(j+1) f[n-j-1][i-1] n^{i-2} $$
,这一式子的意义是:枚举缩点个数\(i\),其中\(i\)包含\(n\),再枚举\(j\)个点与\(n\)一起在缩点\(i\)中;由于考虑圆排列(去除对称)个数为\(\frac{j}{2}\),由于其没有父亲,所以不用乘\(j+1\);然而在Prufer序列最后剩两个点的时候,唯一的一条边可以连接\(j+1\)个点中的任意一个,所以乘以\(j+1\);再将剩下的\(n-1-j\)个点分为有父亲的\(i-1\)个缩点,方案数为\(f[n-j-1][i-1]\);最后乘以Prufer序列个数(注意这里也不能算大小为\(2\)的缩点)
不算大小为\(2\)的缩点的原因:会重复计数。比如下图
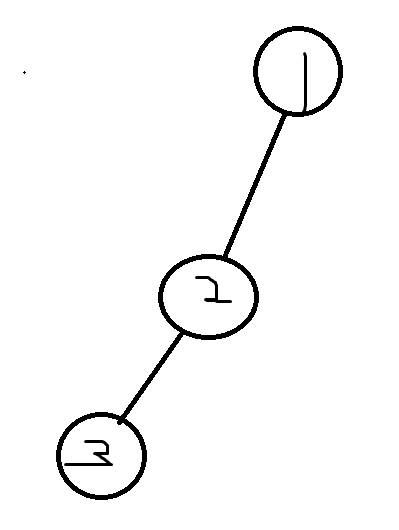
这个仙人掌既有可能在三个点单独为缩点的时候被统计,还有可能在相邻两个点为缩点,另一个点单独成为缩点的时候被统计
没看懂yxc那个代码的思路。。。