EPIC Institute of Technology Round Summer 2024 (Div. 1 + Div. 2) VP记录

EPIC Institute of Technology Round Summer 2024 (Div. 1 + Div. 2) VP记录

A

一眼 \((n - 1) m + 1\)。

B

最后的数列是固定的，每个数与最后数列的数相减后，对差值求和再加上最大值即可。

C

唐诗 C 题，获得 \(3\) 发罚时。

只有一个数右边的数归零了，它才会归零。

右往左扫，如果右边的数已经归零了 \(a_i\) 还不能归零，那么答案设置为 \(a_i\)，否则答案自增。

D

相当于，Alice 选一个数后能删除所有小于或等于它的数，Bob 每回合删除一个数。

所以 Alice 每次取最小的就行了，而 Bob 要考虑的就多了。

考虑目标。Bob 的目标是删除尽量多的数。

设 \(f(i, j)\) 表示前 \(i\) 个数，删 \(j\) 个数后，最多剩多少时间来删 \(j + 1\)。

首先如果不删当前数，则有 \(f(i, j) = f(i - 1, j) + 1\)。

如果删当前数，则有 \(f(i, j) = f(i - 1, j) - cnt_i\)。

直接 dp 即可。

E

设 \(b_u = \sum _{v \in son(u)} a_v - a_u\)，则题目要求的是所有节点的 \(b\) 值不小于 \(0\)。下文简称 \(b\) 值为权值。

那么每次操作就是，选一个节点，令它的权值减去 \(1\) 并令其父节点的权值加上 \(1\)，并且叶子节点的权值是正无穷。

那么当当前考虑的 \(u\) 号节点小于 \(0\) 时，我们需要在它的子树内找一个大于 \(0\) 的节点，然后将它到当前点的链上的节点都操作一遍，然后我们就可以使得当前节点的权值增加而子树内选择的节点减少，并且增加值和减少值相同。每次操作的代价的消耗是链长。

那么贪心的，每次选消耗最小的节点即可。对每个点维护优先队列，按深度从小到大选取，每个点计算完答案后把优先队列合并到父节点上。时间复杂度是 \(O(n ^ 2 \log n)\)。

F

神仙区间 dp。

场上想了一个小时一点不会，狠狠地认识到自己对区间 dp 一无所知。

首先考虑对于一个 \(i\) 它要能被删除要满足的条件。

1. \(a_i \le i\)。显然删除两个值不会让 \(i\) 增大。
2. \(2 | (i - a_i)\)。也是比较显然的。删除两个数不会改变 \(i\) 的奇偶性。
3. 需要在 \([1, i - 1]\) 这个前缀中恰好删除 \(\dfrac {i - a_i} 2\) 个数，使得 \(i = a_i\)。

基于这三个条件，可以进行区间 dp。

设 \(f(l, r)\) 表示如果要把 \([l, r]\) 这段区间删完，至少要在 \([1, i - 1]\) 这个前缀中删除几个数。

首先有种拼接的转移。枚举断点 \(k\)，然后有

\[f(l, r) = \max\left(f(l, k), f(k + 1, r) - \frac {k - l + 1}{2}\right) \]

然后还可以选择将 \(l, r\) 打包删掉。条件是 \(f(l + 1, r - 1) \le \dfrac{l - a_l}2\)。

这里区间 dp 完了后，就能统计答案了。

设 \(g(i)\) 表示前 \(i\) 个数最多进行多少次操作。

枚举 \([1, i]\) 的一段后缀 \([j, i]\)，转移条件是 \(f(j, i) \le g_{j - 1}\)。

然后就做完了。

G

考虑代码之后补，因为周围人在玩 CS。

这种题不看题解不会写，看了题解发现是萌萌分讨题，然后发现不会写笛卡尔树。

参考 [Moeebius 大神的题解](题解：CF1987G2 Spinning Round (Hard Version) - 洛谷专栏 (luogu.com.cn))，或者说单纯在复述/抄袭其题解。

手摸一下，最后建出来的是一棵基环数，具体地，一棵树然后最大值上挂了个自环，否则一定不连通，即无解。具体判断的时候，如果一个非最大值的点套了一个自环，那么就是无解。

然后考虑建出原排列的笛卡尔树，然后注意两种操作。向左连边相当于连向在笛卡尔树上一直往上跳直到第一次向右跳跳上去的那个节点，向右连边则是一直往上跳直到第一次向左跳跳上去的那个节点。

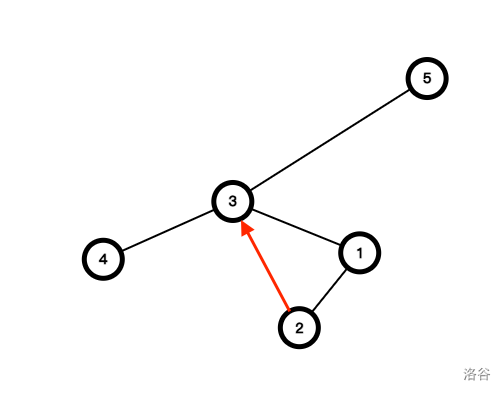
上图是排列 \({2,1,4,3,5}\) 对应的笛卡尔树。\(2\) 号点若向右连边，则会连向 \(3\) 号点。

考虑在笛卡尔树上 dfs 的同时求出直径。

设 \(f(i, 0/1/2)\) 表示 \(i\) 子树内跳出且最后一步对应向 左/右/均有 连边，连边数量的最大值。

对于 \(f(i, 2)\) 要求连出来两条不交的路径。

分讨。

假设现在在点 \(x\)，考虑转移。

1. 路径不经过 \(x\)：

   \[\begin {aligned} f(x, 0) &\leftarrow f(lc_x, 0) \\ f(x, 1) &\leftarrow f(rc_x, 0) \\ f(x, 2) &\leftarrow f(lc_x, 0) + f(rc_x, 1) \end {aligned} \]

   注意到如果左子树向左连边跳出了左子树，那么也一定跳出了当前子树。其余情况同理。

   

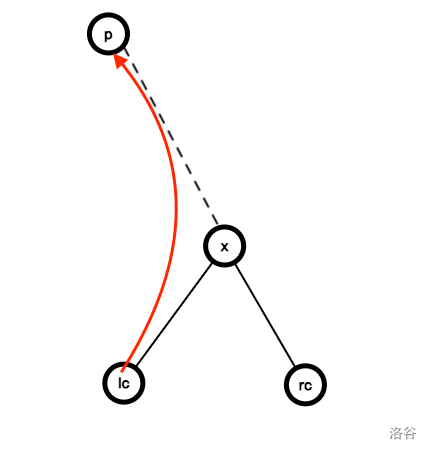
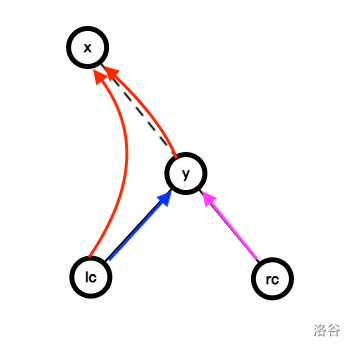
   虚线表示不一定直接相连的点。箭头表示新树上连的边。下同。

2. 路径包含 \(x\)，且 \(x\) 向左连边。

   \[\begin {aligned} f(x, 0) &\leftarrow \max \{f(lc_x, 1), f(rc_x, 0)\} + 1 \\ f(x, 2) &\leftarrow \max \{f(lc_x, 1) + f(rc_x, 1), f(rc_x, 2)\} + 1 \end {aligned} \]

   第一个式子表示从左/右子树跳到了 \(x\)，再进一步跳出去。

   第二个式子，如果存在一左一右两条跳出 \(x\) 的子树的路径，因为 \(x\) 已经向左跳出了，因此子树内仅有可能向右跳出。由于左子树内向右跳只能跳到节点 \(x\)，所以向右跳的路径必然由右子树提供。

   

   

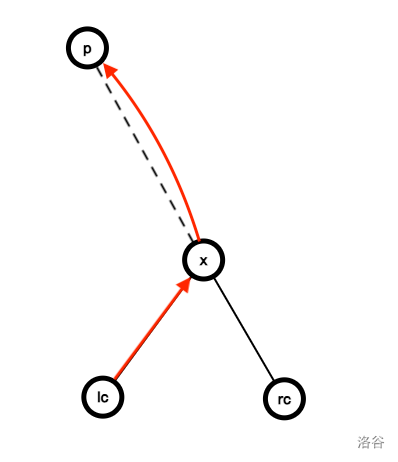
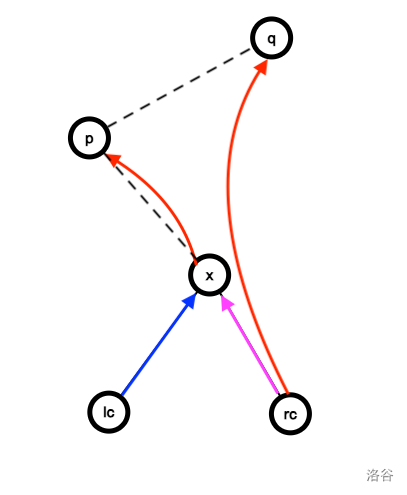
   蓝色，紫色箭头表示二选一。下同。

3. 路径包含 \(x\)，且 \(x\) 向右连边。

   和 2 是镜像的。

---

最后统计答案。记路径两端点的 LCA 为点 \(x\)。

1. 两端点分别属于 \(x\) 的两个子树：

   \[ans \leftarrow f(lc_x, 1) + f(rc_x, 0) \]

2. 两端点来自 \(x\) 的同一子树：

   这种情况不方便在 LCA 处统计答案，因为可能两条边距离 LCA 都很远。

   考虑汇合前最后一次跳跃。

   枚举最后的点最后一次连边的方向。假设是在 \(y\) 处向左连边。有：

   \[ans \leftarrow \max \{f(lc_y, 0) + f(rc_y, 0), f(lc_y, 2)\} + 1 \]

   如图所示。

   

然后就能 \(O(n)\) 解决这个题了。

看起来代码不难写。明天再写？后天再写？谁知道呢。什么时候补这题取决于哪一天 VP 后补题比较快。

H

交互题 + H 题 = 谁爱补谁补去。