前言
纪念一下独立做出来的 \(2400\) 的题
Easy version
思路
先说 \(Easy\) 版本的
我们走路的方式只有可能是这种样子:
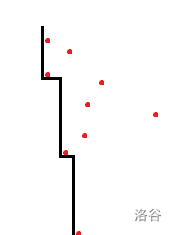
(出处:luogu user FiraCode)
不想手绘图了
即对列排序后,所形成的一个行编号上升的序列
所以 \(Easy\) 就很简单了,对于每一列的最大值,如果大于当前前缀最大值,则它就有贡献
但是如何求 如果鲍勃没有给爱丽丝任何喷泉,那么爱丽丝可以拥有的地块的最大面积 呢?
观察每两个有贡献的点之间的差别,发现其实就是这两个点围成的矩阵及其下方的整个区域
形象化地说,设 \(lx\) 为左边点的行编号,\(ly\) 为左边点的列坐标,\(ry\) 为右边点的列坐标
则贡献为 \([n-(lx+1)+1] \times (ry-ly)\) (可以结合样例给的图理解)
注意最后一个有贡献的点后面的列的贡献需要在最后加一下
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
struct node
{int x,y;int id;bool operator <(const node &o)const{if(y==o.y) return x<o.x;return y<o.y;}
}a[N];
int mx[N];
int ans[N];
signed main()
{int _;cin>>_;while(_--){int n,m,k;cin>>n>>m>>k;for(int i=1;i<=k;i++){scanf("%lld%lld",&a[i].x,&a[i].y);a[i].id=i;ans[i]=0;}sort(a+1,a+1+k);for(int i=1;i<=k;i++) mx[i]=max(mx[i-1],a[i].x);int w=1;a[0].y=1;long long pu=0;int l=1;int r=1; for(int i=1;i<=k;i++){int j=i;while(j<=k&&a[j].y==a[i].y) j++;if(a[j-1].x>mx[i-1]){ans[a[j-1].id]=1;pu+=(n-l+1)*(a[i].y-r);r=a[i].y;l=a[j-1].x+1;} i=j-1;}pu+=(m-r+1)*(n-l+1);printf("%lld\n",pu);for(int i=1;i<=k;i++) printf("%lld ",ans[i]);puts("");}
}
hard version
思路
首先,请确保你已经阅读了 \(Easy\) 版本
然后困难版本让你求如果可以包含当前温泉,问会增加多少贡献
一个重要性质,对于当前贡献点的下一个贡献点,如果去掉了当前贡献点,则下一个贡献点及其后面产生的贡献是不变的
所以对于中间的区域,直接暴力更新即可,因为每个温泉只会被遍历 \(1\) 次,所以复杂度 \(O(n)\)
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
struct node
{int x,y;int id;bool operator <(const node &o)const{if(y==o.y) return x<o.x;return y<o.y;}
}a[N];
int mx[N];
int ans[N];
int id[N];
int sum[N];
signed main()
{int _;cin>>_;while(_--){int n,m,k;cin>>n>>m>>k;for(int i=0;i<=k+5;i++){a[i]={0,0,0};ans[i]=0;id[i]=0;mx[i]=0;sum[i]=0;}for(int i=1;i<=k;i++){scanf("%lld%lld",&a[i].x,&a[i].y);a[i].id=i;}a[k+1]={0,0,0};sort(a+1,a+1+k);for(int i=1;i<=k;i++){if(a[i].x>mx[i-1]){mx[i]=a[i].x;id[i]=i;}else{mx[i]=mx[i-1];id[i]=id[i-1];}}int w=1;a[0].y=1;long long pu=0;int l=1;int r=1; for(int i=1;i<=k;i++){int j=i;while(j<=k&&a[j].y==a[i].y) j++;if(a[j-1].x>mx[i-1]){ans[a[j-1].id]=1;pu+=(n-l+1)*(a[i].y-r);sum[j-1]=pu;r=a[i].y;l+=a[j-1].x-mx[i-1];} i=j-1;}pu+=(m-r+1)*(n-l+1);r=1;l=1;int pre=0;for(int i=1;i<=k;i++){if(!ans[a[i].id]) continue;ans[a[i].id]=sum[pre];int mxx=l-1;if(a[i-1].y==a[i].y&&a[i-1].x>mxx){ans[a[i].id]+=(n-l+1)*(a[i-1].y-r);mxx=a[i-1].x; l=a[i-1].x+1;r=a[i-1].y;pre=i-1;}int f=0;for(int j=i+1;j<=k;j++){if(a[j+1].y==a[j].y) continue;if(a[j].x>mxx){ans[a[i].id]+=(n-l+1)*(a[j].y-r);r=a[j].y;l=a[j].x+1;mxx=a[j].x;}if(ans[a[j].id]==1){ans[a[i].id]=ans[a[i].id]-sum[j];f=1;break;}}if(f==0){ans[a[i].id]+=(m-r+1)*(n-l+1);ans[a[i].id]-=pu;if(ans[a[i].id]<0) ans[a[i].id]=n;}r=a[i].y;l=a[i].x+1;pre=i;}printf("%lld\n",pu);for(int i=1;i<=k;i++) printf("%lld ",ans[i]);puts("");}
}