第2天---RSA基础题型

news/2024/9/18 6:36:29/文章来源:https://www.cnblogs.com/yanxiao777/p/18387725

T1.知pqe求d解m

img

题目：

from Crypto.Util.number import *flag = b'NSSCTF{******}'p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
phi = (p-1)*(q-1)m = bytes_to_long(flag)c = pow(m, e, n)print(f'p = {p}')
print(f'q = {q}')
print(f'e = {e}')
print(f'c = {c}')'''
p = 10554915510546378513140074459658086644656654144905337809416976066414771647836950941616441505897207397834928781511863699153349798682451297889979721668885951
q = 8246403321715011123191410826902524505032643184038566851264109473851746507405534573077909160292816825514872584170252311902322051822644609979417178306809223
e = 65537
c = 40005881669517895877352756665523238535105922590962714344556374248977905431683140065629966778249773228248201807844489945346731806741025157651474530811920115794270396320935022110691338083709019538562205165553541077855422953438117902279834449006455379382431883650004540282758907332683496655914597029545677184720
'''

解题wp以及代码：

from Crypto.Util.number import *
p = 10554915510546378513140074459658086644656654144905337809416976066414771647836950941616441505897207397834928781511863699153349798682451297889979721668885951
q = 8246403321715011123191410826902524505032643184038566851264109473851746507405534573077909160292816825514872584170252311902322051822644609979417178306809223
e = 65537
c = 40005881669517895877352756665523238535105922590962714344556374248977905431683140065629966778249773228248201807844489945346731806741025157651474530811920115794270396320935022110691338083709019538562205165553541077855422953438117902279834449006455379382431883650004540282758907332683496655914597029545677184720n=p*q
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)print(long_to_bytes(m))

T2.知nec解n求m

分解N之后与T1相同

考查：

网站分解N

题目：

from Crypto.Util.number import *flag = b'NSSCTF{******}'p = getPrime(256)
q = getPrime(256)
n = p*q
e = 65537
phi = (p-1)*(q-1)m = bytes_to_long(flag)c = pow(m, e, n)print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')'''
n = 7382582015733895208810490097582153009797420348201515356767397357174775587237553842395468027650317457503579404097373070312978350435795210286224491315941881
e = 65537
c = 6511001389892474870028836129813814173158254564777610289284056550272120510686249909340499673868720839756059423749304765055919251717618117507007046973023557
'''

解题wp以及代码：

用在线网站解密n求解

http://factordb.com/

from Crypto.Util.number import *
n = 7382582015733895208810490097582153009797420348201515356767397357174775587237553842395468027650317457503579404097373070312978350435795210286224491315941881
p = 70538125404512947763739093348083497980212021962975762144416432920656660487657
q = 104660876276442216612517835199819767034152013287345576481899196023866133215633
e = 65537
c = 6511001389892474870028836129813814173158254564777610289284056550272120510686249909340499673868720839756059423749304765055919251717618117507007046973023557n=p*q
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)print(long_to_bytes(m))

T3.知nec解n求m（离线）

考查：

工具解N.(yafu的使用)

题目：

from Crypto.Util.number import *flag = b'NSSCTF{******}'p = getPrime(128)
q = getPrime(128)
n = p*q
e = 65537
phi = (p-1)*(q-1)m = bytes_to_long(flag)c = pow(m, e, n)print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')'''
n = 53690629441472827148854210396580805205350972614395425306316047967905824330731
e = 65537
c = 22130296334673852790451396673112575082637108306697684532954477845025885087040
'''

思路,解题wp以及代码：

思路:求p,q，基础RSA解

我们依然可以尝试使用factordb来分解本题中的n，但是会发现没有得到结果（大部分情况都是得不到的），此时我们观察题目，p和q是两个128位的素数，这个数相比之前我们生成的256或是512素数来说几乎是0（位数多一位，值增加两倍）。

对于这种不算太大的素数，我们可以尝试使用一些工具来分解这个数。

yafu便是这样一种工具，它内置了各种分解算法，能够对不太大或者一些特殊情况下的数进行因式分解。

工具解N

img

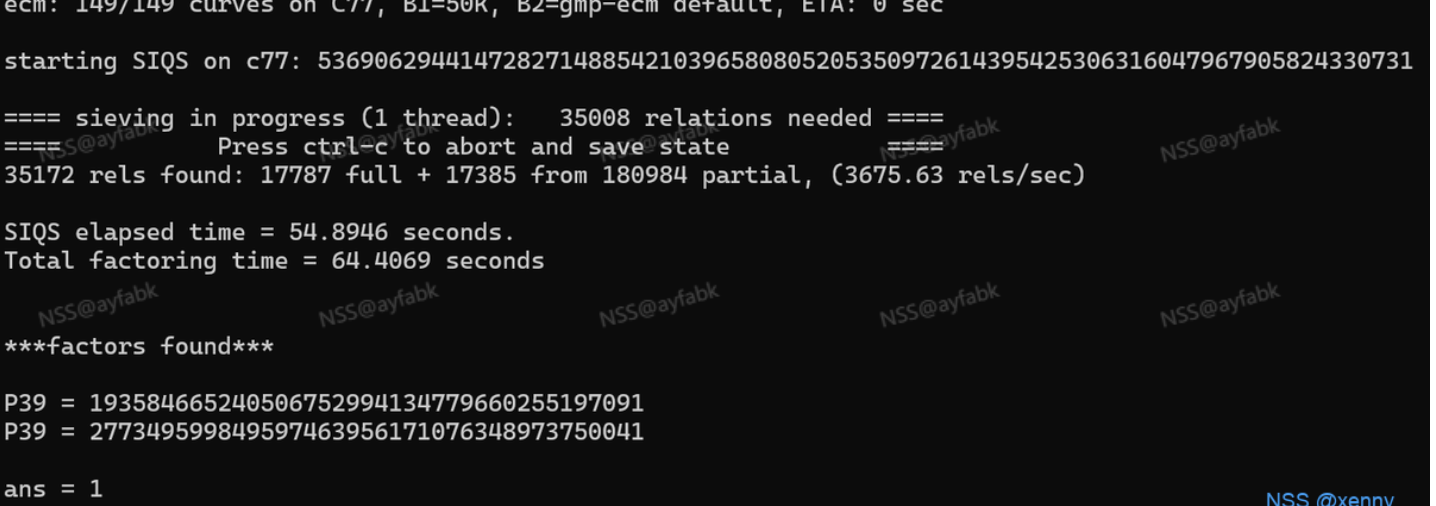
可以看到一共花费了64秒完成了对这个数的分解，上面的其他输出则是yafu采用的分解算法以及参数等内容。

注意：看到速度缓慢，需要耐心等待一下

解题代码：

from Crypto.Util.number import *
n = 53690629441472827148854210396580805205350972614395425306316047967905824330731
p = 193584665240506752994134779660255197091
q = 277349599849597463956171076348973750041
e = 65537
c = 22130296334673852790451396673112575082637108306697684532954477845025885087040n=p*q
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)print(long_to_bytes(m))

知识点与收获：

1.yafu的使用以及下载（离线环境·分解N）

下载地址：https://sourceforge.net/projects/yafu/

在下载好的并解压好的文件夹上鼠标右键打开终端 （例如我的yafu在D:\CTFgoju\yafu）

D:\..CTFgoju\yafu

img

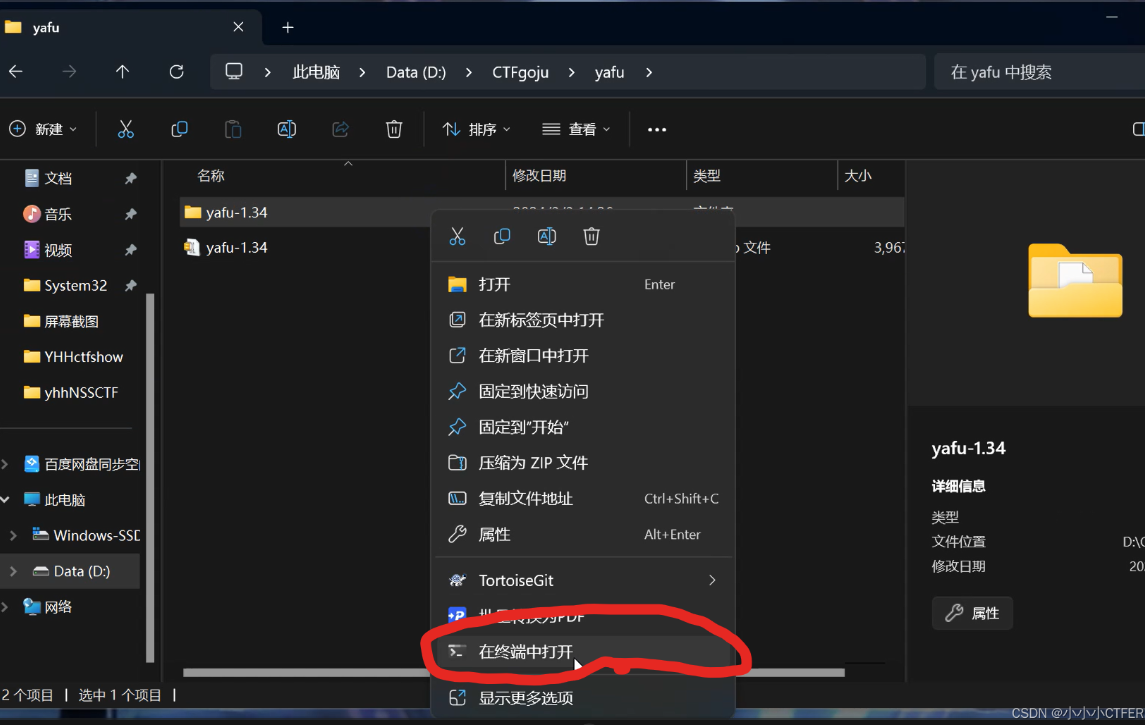
然后输入.\yafu-x64.exe并回车运行

.\yafu-x64.exe

来到这个页面就OK了

img

然后输入

factor(N)

N是你想分解的数，等一下就出来了

T4.知pq为相邻素数

题目：

from Crypto.Util.number import *
import gmpy2
flag = b'NSSCTF{******}'p = getPrime(512)
q = gmpy2.next_prime(p)
n = p*q
e = 65537
phi = (p-1)*(q-1)m = bytes_to_long(flag)c = pow(m, e, n)print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')'''
n = 115637000420176820831322601039129424406844427046456738651883381559357542765613732363445112111006849040385859313572091386802534464534403117787314180179562651607533039692795522388596550968316951090748054495960090527479954143448774136390568881020918710834542819900918984139672802889774720153267841255456602500057
e = 65537
c = 98161406745910866780822530171878255235776133393411573803496865047700715941955255328757920065032397556905095591171977170479344602512244671081108703687450560269408412671849929423399172588599903975793985819498354819305128607934552101433664794909855378636055525016664559476808490723554481335856183927702549281730
'''

关键步骤

p = getPrime(512)
q = gmpy2.next_prime(p)

代码解读

  1. **p = getPrime(512)**

这行代码调用 getPrime 函数，并传入参数 512。这个参数通常指定了要生成的素数的位数（以二进制位为单位）。因此，getPrime(512) 的目的是生成一个大约 512 位长的随机素数，并将其赋值给变量 p。由于 getPrime 不是标准库函数，我们无法直接知道它的具体实现细节，但可以合理推测它使用了某种形式的随机数生成和素数测试算法来确保生成的数是素数。

  1. **q = gmpy2.next_prime(p)**

这行代码使用 gmpy2 库的 next_prime 函数，该函数接受一个整数作为输入，并返回该整数之后的下一个素数。在这里，它接受 p（即之前通过 getPrime 函数生成的 512 位素数）作为输入，并找到并返回 p 之后的下一个素数，然后将这个素数赋值给变量 q。

代码学习：

p = getPrime(512)
q = gmpy2.next_prime(p)

生成一个512位的质数p;

生成大于p的下一位指数为q

（详细的在blog）

考查：

1.解pq，求d求明文；

2.相邻素数pq由n开方解pq

img

解题wp以及代码：

1.思路::求p,q，基础RSA解

就是用开平方解其中一个素数，然后用n解另外一个素数，之后正常解RSA

2.wp

题目生成了一个512位的素数p，随后使用next_prime函数获取p的下一个素数作为q，然后再做RSA算法，本题素数都比较大，我们没办法直接分解这个素数。但是我们发现p和q之间似乎有一些联系，他们太接近了，素数在自然数中其实没那么少，我们可以进行测试:

from Crypto.Util.number import *
import gmpy2
p = getPrime(512)
q = gmpy2.next_prime(p)
print(q-p)

你会发现大部分情况下二者的差值都小于1000，那么有这层关系我们如何解题呢。考虑n的算术平方根为sn，同时sn也是p和q的几何平均值。此时则有

img

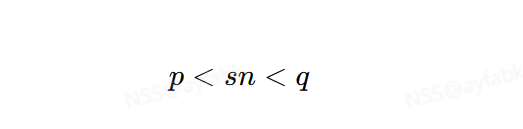
我们又有q,p是相邻的素数，p的下一个素数为q，同理也有sn的下一个素数也应该是q，到这里你或许应该知道我们该怎么操作了。但是如何编写代码求平方根呢，这里我们借助gmpy2中的isqrt函数，在后续我们更多的会使用gmpy2而不是Crypto中的数学函数（因为二者速度不是一个量级）。

sn = isqrt(n)
q = next_prime(sn)
p = n // q

注意除的时候需要用整除。（用/的话会科学计数法，无法进行计算）

3.代码：

from Crypto.Util.number import *
from gmpy2 import *
p = getPrime(512)
q = gmpy2.next_prime(p)n = 115637000420176820831322601039129424406844427046456738651883381559357542765613732363445112111006849040385859313572091386802534464534403117787314180179562651607533039692795522388596550968316951090748054495960090527479954143448774136390568881020918710834542819900918984139672802889774720153267841255456602500057
e = 65537
c = 98161406745910866780822530171878255235776133393411573803496865047700715941955255328757920065032397556905095591171977170479344602512244671081108703687450560269408412671849929423399172588599903975793985819498354819305128607934552101433664794909855378636055525016664559476808490723554481335856183927702549281730sn = isqrt(n)
q = next_prime(sn)
p = n // qphi = (p-1)*(q-1)
d = invert(e, phi)m = pow(c, d, n)
print(long_to_bytes(m))

扩展

直接工具分解也行，但是需要了解原理，以便后面进阶。

imgimg

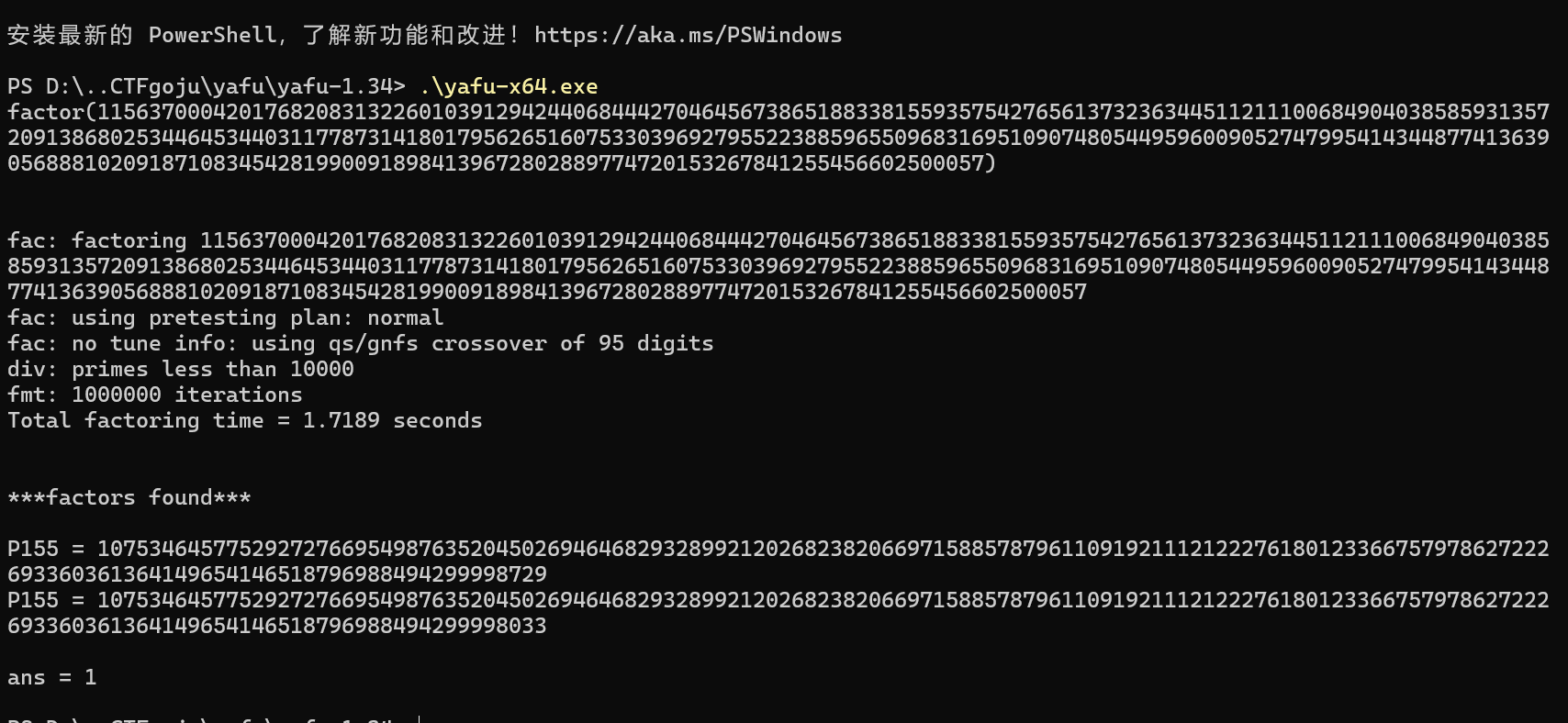
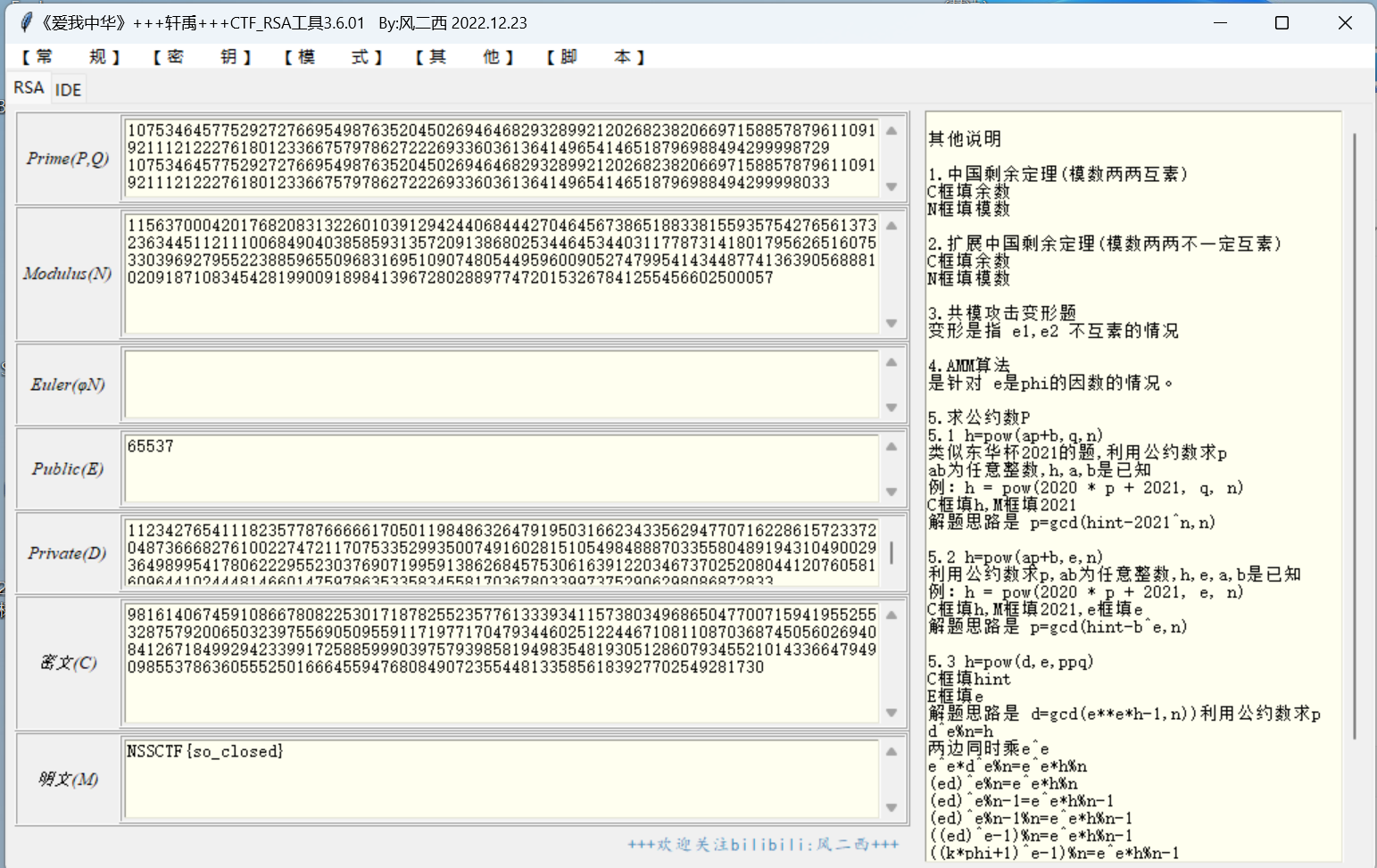
T5.知pq相近--费马分解

一.题目：

from Crypto.Util.number import *
import gmpy2
flag = b'NSSCTF{******}'p = getPrime(512)
q = gmpy2.next_prime(p - getPrime(256))
n = p*q
e = 65537
phi = (p-1)*(q-1)
m = bytes_to_long(flag)
c = pow(m, e, n)print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
'''
n = 148841588941490812589697505975986386226158446072049530534135525236572105309550985274214825612079495930267744452266230141871521931612761645600600201983605957650711248808703757693378777706453580124982526368706977258199152469200838211055230241296139605912607613807871432800586045262879581100319519318390454452117
e = 65537
c = 69038543593219231496623016705860610154255535760819426453485115089535439537440188692852514795648297200067103841434646958466720891016026061658602312900242658759575613625726750416539176437174502082858413122020981274672260498423684555063381678387696096811975800995242962853092582362805345713900308205654744774932
'''

关键步骤

p = getPrime(512)
q = gmpy2.next_prime(p - getPrime(256))

二.考查：费马分解

条件：p，q相近

img

img

详细介绍
https://blog.csdn.net/hacker_zrq/article/details/121444869

三.解题wp以及代码：

思路:求p,q，基础RSA解

代码：

from Crypto.Util.number import *
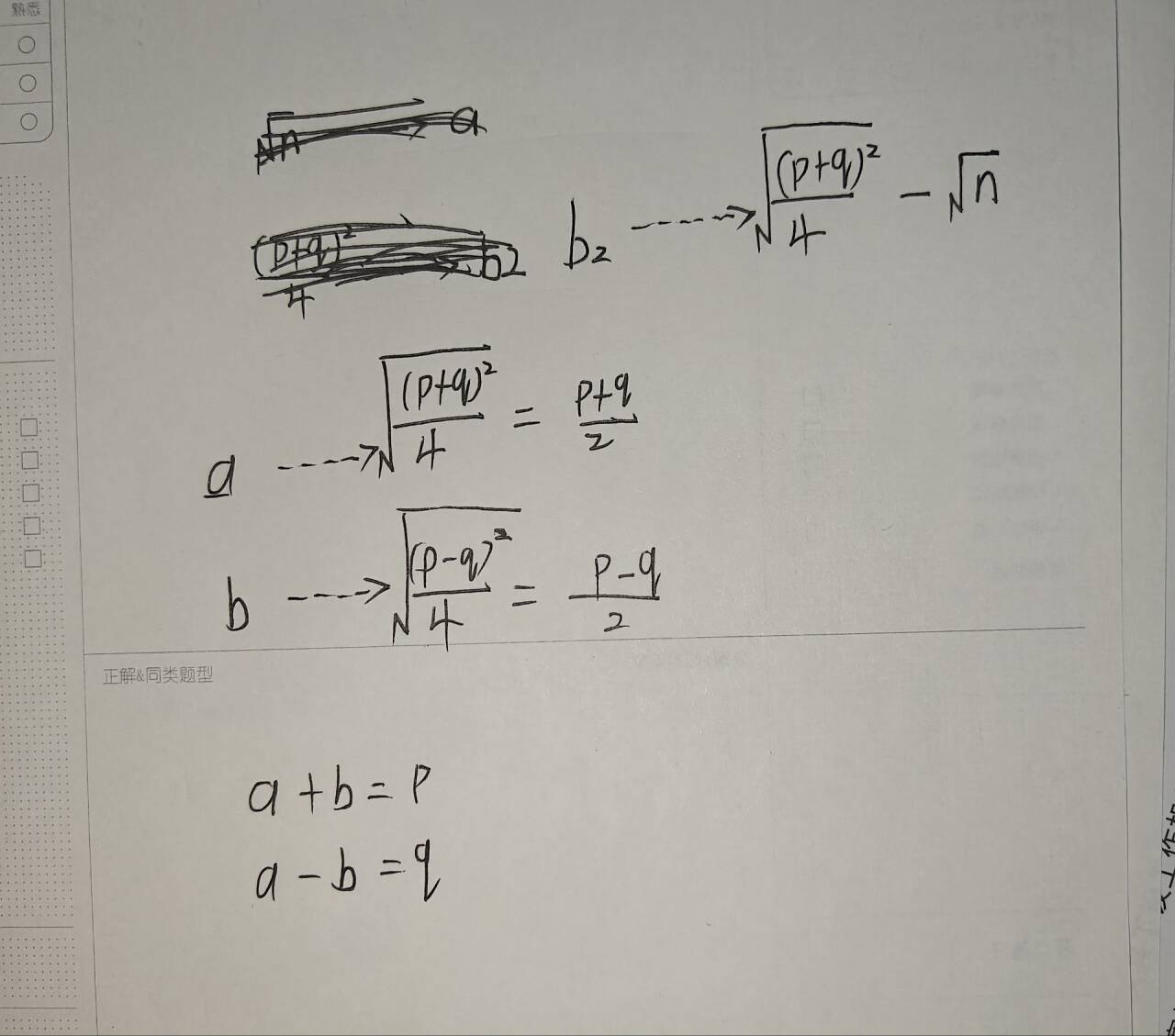
from gmpy2 import *def fermat_attack(n):a = isqrt(n)b2 = a*a - nb = isqrt(n)while b*b != b2:a = a + 1b2 = a*a - nb = isqrt(b2)p = a+bq = a-bassert n == p * qreturn p, qn = 148841588941490812589697505975986386226158446072049530534135525236572105309550985274214825612079495930267744452266230141871521931612761645600600201983605957650711248808703757693378777706453580124982526368706977258199152469200838211055230241296139605912607613807871432800586045262879581100319519318390454452117
e = 65537
c = 69038543593219231496623016705860610154255535760819426453485115089535439537440188692852514795648297200067103841434646958466720891016026061658602312900242658759575613625726750416539176437174502082858413122020981274672260498423684555063381678387696096811975800995242962853092582362805345713900308205654744774932p, q = fermat_attack(n)
phi = (p-1)*(q-1)
d = invert(e, phi)m = pow(c, d, n)
print(long_to_bytes(m))

帮助代码理解

img

T6.共享素数

一.题目：

from Crypto.Util.number import *
flag = b'NSSCTF{******}'p1 = getPrime(512)
q = getPrime(512)
p2 = getPrime(512)n1 = p1*q
n2 = p2*qe = 65537m = bytes_to_long(flag)
c1 = pow(m, e, n1)
c2 = pow(m, e, n2)print(f'n1 = {n1}')
print(f'n2 = {n2}')
print(f'e = {e}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
'''
n1 = 143348646254804947818644803938588739009782265465565896704788366218178523508874903492905378927641178487821742289009401873633609987818871281146199303052141439575438691652893995423962176259643151111739185844059243400387734688275416379337335777994990138009973618431459431410429980866760075387393812720247541406893
n2 = 138110854441015362783564250048191029327770295545362614687087481715680856350219966472039006526758450117969049316234863489558254565946242898336924686721846675826468588471046162610143748100096038583426519355288325214365299329095841907207926280081868726568947436076663762493891291276498567791697978693639037765169
e = 65537
c1 = 54957154834913405861345262613986460384513988240935244315981524013378872930144117440787175357956479768211180412158274730449811947349624843965933828130932856052315165316154486515277625404352272475136003785605985702495858150662789554694910771308456687676791434476722168247882078861234982509648037033827107552029
c2 = 122221335585005390437769701090707585780333874638519916373585594040154234166935881089609641995190534396533473702495240511296379249872039728112248708182969185010334637138777948970821974238214641235158623707766980447918480715835847907220219601467702961667091318910582445444058108454023108157805147341928089334736
'''

关键步骤：

三个素数加密m

p1 = getPrime(512)
q = getPrime(512)
p2 = getPrime(512)n1 = p1*q
n2 = p2*q

二.解题wp以及代码：

思路:求p,q，基础RSA解

就是共享素数了，用n1，n2可以求出共享的素数，随之而来就可以用最小公因数求p，q解RSA,m加密了两组，随便解密一组就行

解题代码：

关键步骤

用gcd求解最小公因数

q = gcd(n1, n2) //需要引入库from gmpy2 import *
from Crypto.Util.number import *
from gmpy2 import *n1 = 143348646254804947818644803938588739009782265465565896704788366218178523508874903492905378927641178487821742289009401873633609987818871281146199303052141439575438691652893995423962176259643151111739185844059243400387734688275416379337335777994990138009973618431459431410429980866760075387393812720247541406893
n2 = 138110854441015362783564250048191029327770295545362614687087481715680856350219966472039006526758450117969049316234863489558254565946242898336924686721846675826468588471046162610143748100096038583426519355288325214365299329095841907207926280081868726568947436076663762493891291276498567791697978693639037765169
e = 65537
c1 = 54957154834913405861345262613986460384513988240935244315981524013378872930144117440787175357956479768211180412158274730449811947349624843965933828130932856052315165316154486515277625404352272475136003785605985702495858150662789554694910771308456687676791434476722168247882078861234982509648037033827107552029
c2 = 122221335585005390437769701090707585780333874638519916373585594040154234166935881089609641995190534396533473702495240511296379249872039728112248708182969185010334637138777948970821974238214641235158623707766980447918480715835847907220219601467702961667091318910582445444058108454023108157805147341928089334736q = gcd(n1, n2)
p1 = n1 // q
phi = (p1-1)*(q-1)
d = invert(e, phi)m = pow(c1, d, n1)
print(long_to_bytes(m))

TTTT6.5欧拉函数详细介绍

这里放两个定理，以便后面求欧拉函数用

定理一.多个素数求欧拉

img

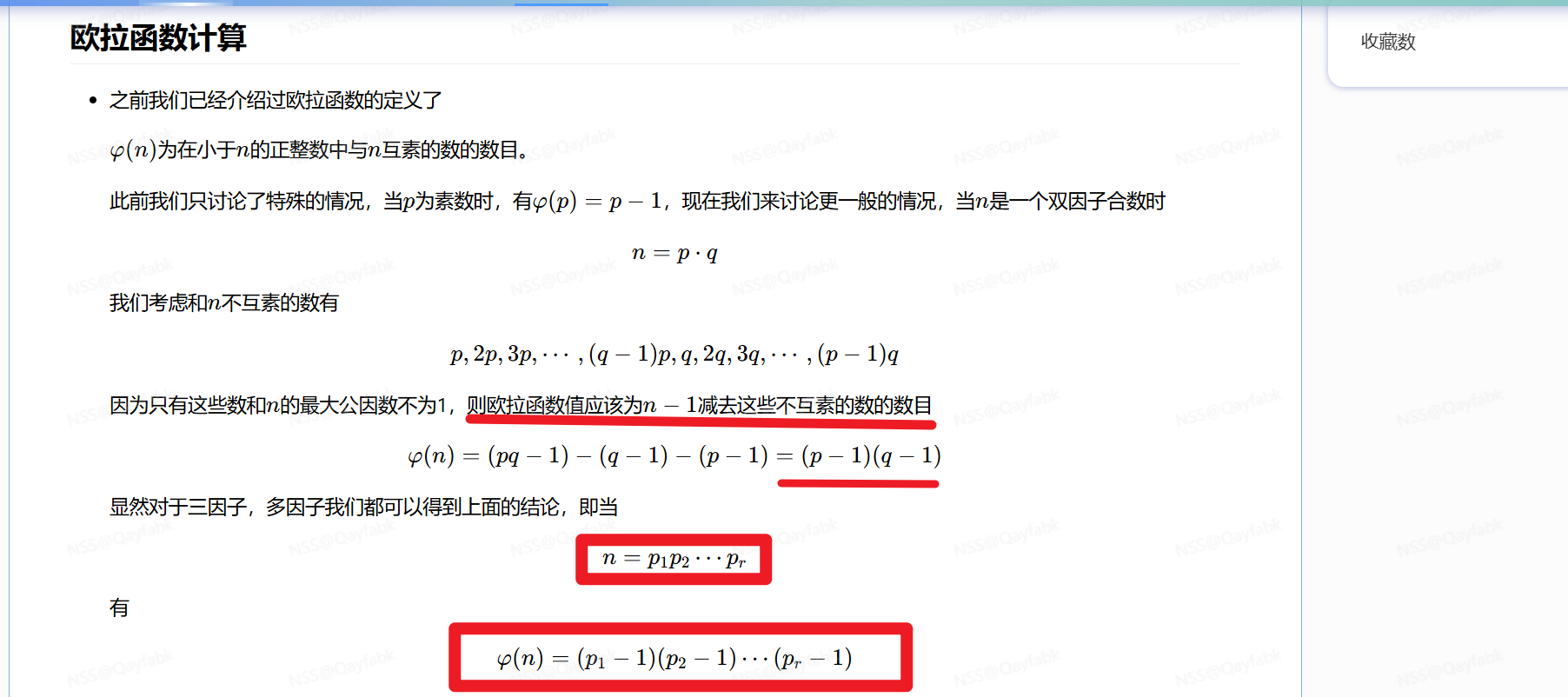
定理二.高阶因子求欧拉

img

弄不懂就记下来，后面再学习

扩展

欧拉定理

img

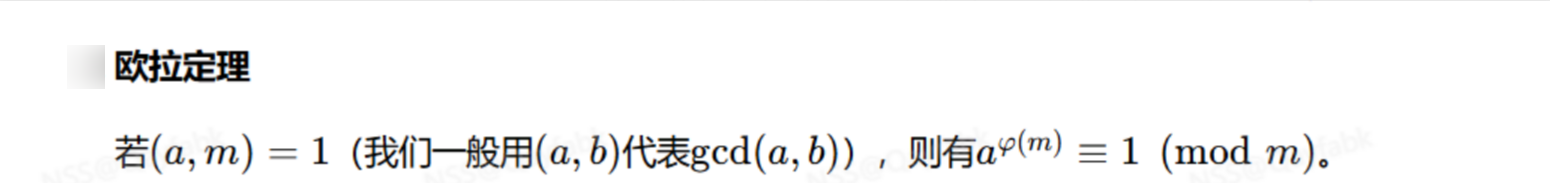
扩展欧拉定理

img

T7.多个素数求欧拉

一.题目：

from Crypto.Util.number import *flag = b'NSSCTF{******}' + b'1'*170p = getPrime(512)
q = getPrime(512)
r = getPrime(512)
n = p*q*r
e = 65537
phi = (p-1)*(q-1)*(r-1)m = bytes_to_long(flag)c = pow(m, e, n)print(f'p = {p}')
print(f'q = {q}')
print(f'r = {r}')
print(f'e = {e}')
print(f'c = {c}')'''
p = 10666139331774428325755287635566473140804481321882464031499529816800186578792308674238646794969384836340484775213796013129603472328582005363876462361316357
q = 8419311673449738061914489023962717718536471719688567807316495262754711350004888752049108347226115000749280146228195893953964759818878155006622123533942989
r = 12875078327453384158245832541544758526474680184252540739652077682353277702054275525591573258723948221345537075374635382175740236093131628077747126356403959
e = 65537
c = 424552463648937499189041230155623101311087334789253159440707211761796081289342164253743235182597460622581134089949035117444838205449163269030784233435435681797627188717450074808905561404960693227573181548281296514743775615606388692910356320667720308219275107443303501165027740512539959960217657836317351146520079753390346207659007421416917274795119021374032194294225350901136669304225010974617136606299060486198480556729770211945777266366417547752798441211059402
'''

关键步骤：多个因子求欧拉函数

p = getPrime(512)
q = getPrime(512)
r = getPrime(512)
n = p*q*r
e = 65537
phi = (p-1)*(q-1)*(r-1)

二.解题wp以及代码：

1.思路:求欧拉函数，其他不变，基础RSA解

img

2.wp：

假如遇分解时多个因子时使用，或者出题直接给就秒

3.代码：

from Crypto.Util.number import *p = 10666139331774428325755287635566473140804481321882464031499529816800186578792308674238646794969384836340484775213796013129603472328582005363876462361316357
q = 8419311673449738061914489023962717718536471719688567807316495262754711350004888752049108347226115000749280146228195893953964759818878155006622123533942989
r = 12875078327453384158245832541544758526474680184252540739652077682353277702054275525591573258723948221345537075374635382175740236093131628077747126356403959
e = 65537
c = 424552463648937499189041230155623101311087334789253159440707211761796081289342164253743235182597460622581134089949035117444838205449163269030784233435435681797627188717450074808905561404960693227573181548281296514743775615606388692910356320667720308219275107443303501165027740512539959960217657836317351146520079753390346207659007421416917274795119021374032194294225350901136669304225010974617136606299060486198480556729770211945777266366417547752798441211059402n=p*q*r
phi = (p-1)*(q-1)*(r-1)
d = inverse(e, phi)
m = pow(c, d, n)print(long_to_bytes(m))

T8.高阶因子求欧拉

一.题目：

from Crypto.Util.number import *flag = b'NSSCTF{******}' + b'1'*100p = getPrime(256)
q = getPrime(256)
n = (p**3) * q
e = 65537
phi = (p-1)*(q-1)m = bytes_to_long(flag)c = pow(m, e, n)print(f'p = {p}')
print(f'q = {q}')
print(f'e = {e}')
print(f'c = {c}')'''
p = 80505091208742938705306670241621545375764148093711243653439069254008824979403
q = 67599990875658931406915486208971556223245451500927259766683936131876689508521
e = 65537
c = 7958690969908064264211283192959937430539613460471121984649054121171267262097603091410178042319139582772142226087020110084551158367679146616732446561228522673699836019156243452069036383047309578614662564794584927846163157472211089368697387945469398750955336949678910159585015004994620777231073804301249774041
'''

关键步骤：

p = getPrime(256)
q = getPrime(256)
n = (p**3) * q
e = 65537
phi = (p-1)*(q-1)

还是欧拉定理的扩展，遇到因子p，q大于一次方就秒

二.解题wp以及代码：

1.思路:求欧拉函数，其他不变，基础RSA解

img

（这里不懂的，去看欧拉函数介绍）

2.代码：

from Crypto.Util.number import *p = 80505091208742938705306670241621545375764148093711243653439069254008824979403
q = 67599990875658931406915486208971556223245451500927259766683936131876689508521
e = 65537
c = 7958690969908064264211283192959937430539613460471121984649054121171267262097603091410178042319139582772142226087020110084551158367679146616732446561228522673699836019156243452069036383047309578614662564794584927846163157472211089368697387945469398750955336949678910159585015004994620777231073804301249774041n = (p**3)*q
phi = (p**2)*(p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)print(long_to_bytes(m))

结语：

本来想着写10题的今天，但是有一些地方时间用超了，明天再继续写吧，不能水，睡觉

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/789402.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

带记忆的对话api上线

带记忆的对话api上线

Link.AI 记忆对话 API原生支持开发者在应用/工作流中设置的记忆功能。开发者无需自行维护上下文记忆并通过messages参数传递，只需传入用户问题和身份标识即可，由系统按用户维度对上下文记忆进行维护，从而实现长期记忆下的多轮对话。API 简介 Link.AI 已为开发者提供了调用智…
阅读更多...
devexpress 组件使用研究

devexpress 组件使用研究

1.提示框private void textEdit1_KeyPress(object sender, KeyPressEventArgs e) { if (e.KeyChar == ( char)Keys.Enter) { AlertControl alert = new AlertControl(); alert.Show(this, "提示", textEdit1.Text, true);} }
阅读更多...
Vue2实现应用添加水印的功能

Vue2实现应用添加水印的功能

需求 有的情况，我们需要给我们的网页添加水印。我们可以使用第三方库Watermark Design。官方地址：https://watermark-design.github.io/watermark/zh/ 效果示例代码 入口文件main.js import WatermarkDesign from @watermark-design/vue; Vue.use(WatermarkDesign)vue容器App…
阅读更多...
Hive源码解析

Hive源码解析

1.概述 Apache Hive是一款建立在Hadoop之上的数据仓库工具，它提供了类似于SQL的查询语言，使得用户能够通过简单的SQL语句来处理和分析大规模的数据。本文将深入分析Apache Hive的源代码，探讨其关键组件和工作原理，以便更好地理解其在大数据处理中的角色。 2.内容 在开始源代…
阅读更多...
芒格-“用幸存者心态去对待问题，永远不要有受害者心态”

芒格-“用幸存者心态去对待问题，永远不要有受害者心态”

我不会因为人性而感到意外，也不会花太多时间感受背叛， 我总是低下头去调整自己，去适应这一类事情， 所以我不允许自己花太多时间，去感受背叛， 但凡有一丁点这种想法，从我脑海闪过，我就马上规避掉了， 我不喜欢任何成为受害者的感觉， 我认为这是一种反其道而行之的人类思…
阅读更多...
列表渲染

列表渲染

阅读更多...
三分钟总结开源流程表单的优势特点

三分钟总结开源流程表单的优势特点

今天一起来看看开源流程表单的优势特点，一起了解它为何能助力企业降本增效。实现流程化办公，可以借助低代码技术平台、开源流程表单的优势特点。作为当前较为理想的平台产品，低代码技术平台凭借够灵活、好操作、可视化界面的优势特点，得到了通信业、医疗、高校等很多行业客…
阅读更多...
使用zig语言制作简单博客网站（六）文章详情页

使用zig语言制作简单博客网站（六）文章详情页

前端代码前端代码 <!DOCTYPE html> <html lang="zh-CN"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><link rel="stylesheet" …
阅读更多...
条件渲染

条件渲染

阅读更多...
为何选择合适的文档管理系统至关重要？

为何选择合适的文档管理系统至关重要？

国内外主流的 10 款文档管理系统对比：1.PingCode；2.Worktile；3.飞书文档；4.石墨文档；5.语雀；6.Google Docs；7.Dropbox Business；8.Confluence；9.Microsoft OneDrive；10.Box。在当今快速发展的商业环境中，众多企业面临的一个主要挑战是如何有效管理日益增长的文件和数…
阅读更多...
黑神话悟空-前所未有的团结

黑神话悟空-前所未有的团结

阅读更多...
Vue3的学习---11

Vue3的学习---11

11. Vue组合式API 11.1 为什么要使用Composition API 11.1.1 一个Options API实例 在前面都是采用Options API（基于选项的API）来些一个组件，下面是一个实例 <template>num：{{ num }}<br>double：{{ double }}<button @click="add">加</butt…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023