堆栈
定义
栈(stack) 是一种遵循先入后出逻辑的线性数据结构,常见操作入栈,出栈,访问栈
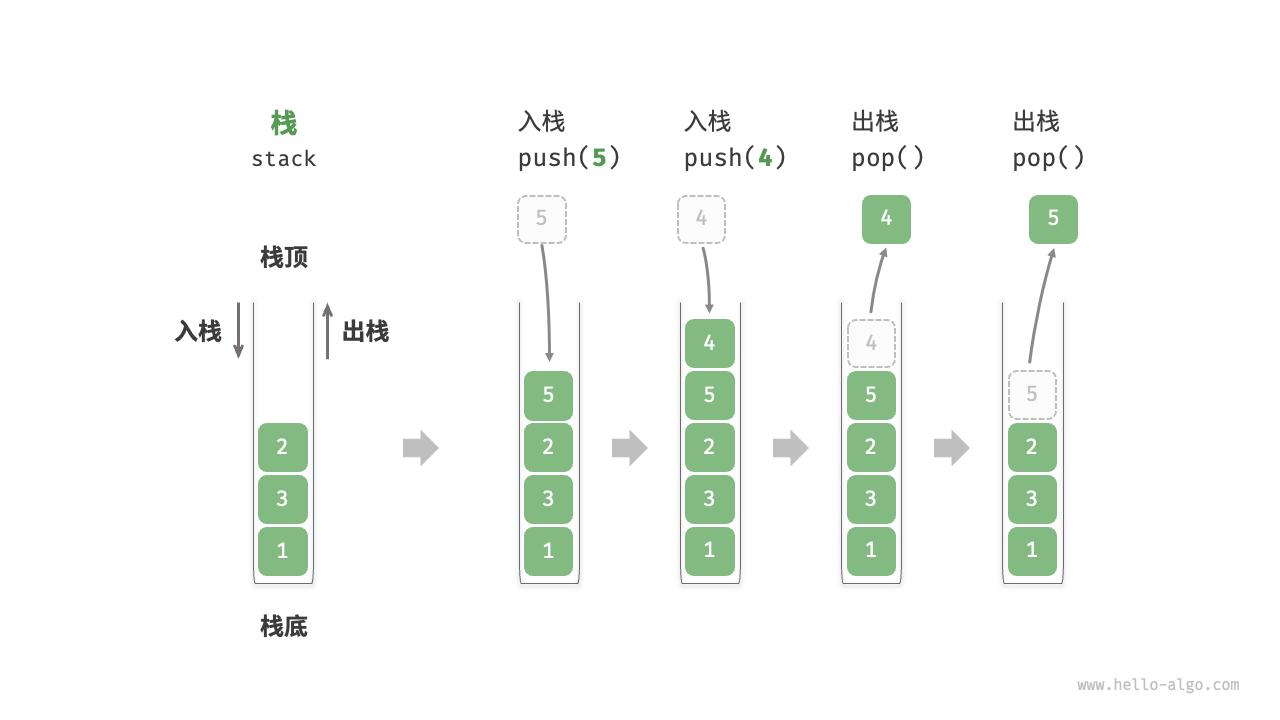
图片来源:https://www.hello-algo.com/
栈的实现
栈遵循先入后出的原则,因此我们只能在栈顶添加或删除元素。然而,数组和链表都可以在任意位置添加和删除元素,因此栈可以视为一种受限制的数组或链表。换句话说,我们可以“屏蔽”数组或链表的部分无关操作,使其对外表现的逻辑符合栈的特性。
基于链表的实现
使用链表实现栈时,我们只需将链表的头节点视为栈顶,尾节点视为栈底
入栈操作,只需将元素插入链表头部(这种节点插入方式被称为“头插法”),出栈操作,只需将头结点从链表中删除即可。
/* 基于链表实现的栈 */
typedef struct
{ListNode *top; // 将头节点作为栈顶int size; // 栈的长度
} LinkedListStack;/* 构造函数 */
LinkedListStack *newLinkedListStack()
{LinkedListStack *s = malloc(sizeof(LinkedListStack));s->top = NULL;s->size = 0;return s;
}/* 析构函数 */
void delLinkedListStack(LinkedListStack *s)
{while (s->top){ListNode *n = s->top->next;free(s->top);s->top = n;}free(s);
}/* 获取栈的长度 */
int size(LinkedListStack *s)
{return s->size;
}/* 判断栈是否为空 */
bool isEmpty(LinkedListStack *s)
{return size(s) == 0;
}/* 入栈 */
void push(LinkedListStack *s, int num)
{ListNode *node = (ListNode *)malloc(sizeof(ListNode));node->next = s->top; // 更新新加节点指针域node->val = num; // 更新新加节点数据域s->top = node; // 更新栈顶s->size++; // 更新栈大小
}/* 访问栈顶元素 */
int peek(LinkedListStack *s)
{if (s->size == 0){printf("栈为空\n");return INT_MAX;}return s->top->val;
}/* 出栈 */
int pop(LinkedListStack *s)
{int val = peek(s);ListNode *tmp = s->top;s->top = s->top->next;// 释放内存free(tmp);s->size--;return val;
}基于数组的实现
使用数组实现栈时,可以将数组的尾部作为栈顶,入栈,出栈分别在尾部添加与删除元素,时间复杂度为O(1);
由于入栈元素可能会源源不断的增加,使用动态数组操作可避免后续增容操作
/* 基于数组实现的栈 */
typedef struct
{int *data;int size;
} ArrayStack;/* 构造函数 */
ArrayStack *newArrayStack()
{ArrayStack *stack = malloc(sizeof(ArrayStack));// 初始化一个大容量,避免扩容stack->data = malloc(sizeof(int) * MAX_SIZE);stack->size = 0;return stack;
}/* 析构函数 */
void delArrayStack(ArrayStack *stack)
{free(stack->data);free(stack);
}/* 获取栈的长度 */
int size(ArrayStack *stack)
{return stack->size;
}/* 判断栈是否为空 */
bool isEmpty(ArrayStack *stack)
{return stack->size == 0;
}/* 入栈 */
void push(ArrayStack *stack, int num)
{if (stack->size == MAX_SIZE){printf("栈已满\n");return;}stack->data[stack->size] = num;stack->size++;
}/* 访问栈顶元素 */
int peek(ArrayStack *stack)
{if (stack->size == 0){printf("栈为空\n");return INT_MAX;}return stack->data[stack->size - 1];
}/* 出栈 */
int pop(ArrayStack *stack)
{int val = peek(stack);stack->size--;return val;
}
/* 测试代码 */
int main()
{ArrayStack *stack = newArrayStack();push(stack, 1);push(stack, 2);push(stack, 3);printf("%d\n", pop(stack));printf("%d\n", pop(stack));printf("%d\n", pop(stack));printf("%d\n", pop(stack));delArrayStack(stack);return 0;
}
典型应用
- 浏览器的后退与前进,软件中的撤销和反撤销
- 程序内存管理
- 深度优先算法,回溯算法
- 后缀表达式取值